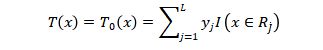数据分析课程设计(数学建模+数据分析+数据可视化)——利用Python开发语言实现以及常见数据分析库的使用

目录

数据分析报告——基于贫困生餐厅消费信息的分类与预测

一、数据分析背景以及目标

二、分析方法与过程

数据探索性与预处理

合并文件并检查缺失值

2.计算文件的当中的值

消费指数的描述性分析

首先对数据进行标准化处理

聚类模型的评价

聚类模型的结果关联

利用决策树模型进行预测

决策数模型的数据处理

决策树模型的参数设置

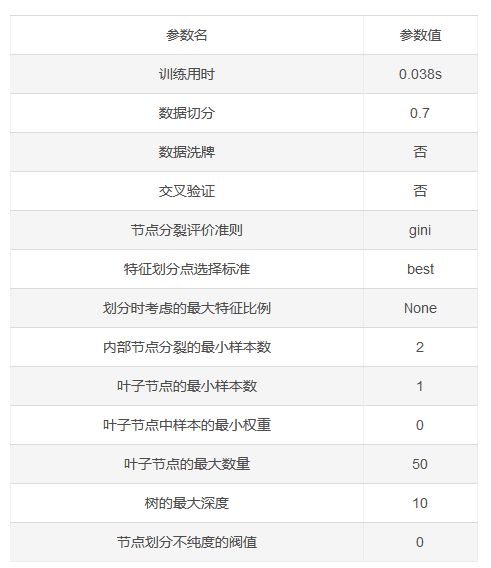
模型参数如下表：

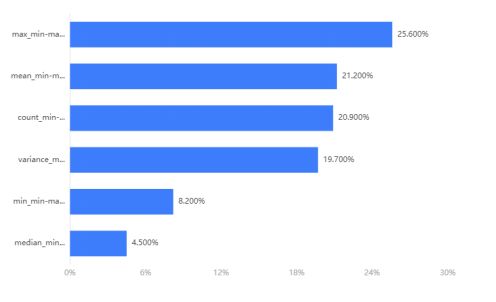
特征重要性：

决策树算法思想

模型评价

gitee代码以及数据文件

---

数据分析报告——基于贫困生餐厅消费信息的分类与预测

摘要

近年来，随着精准资助的不断推进以及信息化技术的不断提升，本文通过对学生的餐厅消费数据进行数据分析，利用数据可视化、数学建模、机器学习算法，借助Python进行算法实现，隐蔽地认定困难学生，并通过隐蔽的方式给予适度的资助补偿，进一步完善精准资助机制。

首先进行数据预处理，根据附件中的数据，删除不相关数据、缺失补全、特征提取等。根据附件1-3中该组学生不同学年的日三餐餐厅消费金额数据记录

，建立聚类模型并利用Python数据可视化，得出三种不同代表性群体，从中发现一般贫困学生类别的未消费数量波动、消费次数总和下降、平均消费金额上升以及消费金额中位数逐年增长；特别贫困学生类别的未消费数量增加、消费次数总和波动、平均消费金额上升以及消费金额中位数波动；不贫困学生类别的未消费数量增加、消费次数总和下降、平均消费金额存在波动以及消费金额中位数波动等规律。这些变化可能受到多种因素的影响，例如经济情况、学生消费行为变化等。

结合已有数据，进行分析并进行数据可视化展示，根据附件8给出部分同学第一学年后经其他方式认定的贫困程度等级结合第一问得出的影响因素，建立决策树模型，依据附件1-3消费行为预测贫困程度，并对附件9进行补充。其中一般贫困为53、240、768、1081、1422、1494、1836、2099、2103、2527、2889、2972、3155、3247、3346、3353、3356、3694、3710、3870、4068共计21名同学，特别贫困1043、1613等2名同学，其余为不贫困同学。训练集的准确率为0.792，测试集的准确率为0.721。

本文研究了餐厅消费数据与学生家庭贫困程度之间的关联，并通过多种数据分析方法进行数据分析和预测，帮助高校更准确地判断学生家庭经济困难程度，具有实际应用价值和可推广性，并进行了相关优化，提高高校资助工作的效率和精准性。

[关键词]    聚类模型  决策树模型  数据分析 数据标准化 学生资助  

一、数据分析背景以及目标

随着精准资助政策的推广，如何更准确地判断家庭经济困难程度，已经成为高校资助工作中不可忽视的重要问题。针对此问题，本文将餐厅消费数据进行分析和研究，以探究消费行为和学生家庭贫困程度之间的关联。

本文通过对附件0性别信息，附件1-3是该组学生不同学年的日三餐餐厅消费金额数据记录（部分），附件4-7同时给出了其中部分同学的饮食种类信息的处理，达成以下分析目标：

1.建立模型并利用Python数据可视化，得出不同代表性群体，定量分析该群体三学年的主要消费行为特征变化规律。根据附件1-3中该组学生不同学年的日三餐餐厅消费金额数据记录，以及附件4-7同学的饮食种类信息。

2.结合已有数据分析并进行数据可视化展示，根据附件8给出部分同学第一学年后经其他方式认定的贫困程度等级 ，建立数学模型依据附件1-3消费行为预测贫困程度。

二、分析方法与过程

首先进行数据预处理，根据附件的数据，我们需要对数据进行必要的预处理。具体地，删除不相关数据、缺失补全、特征提取等，以便建立数学模型以及使用机器算法模型得出结论。

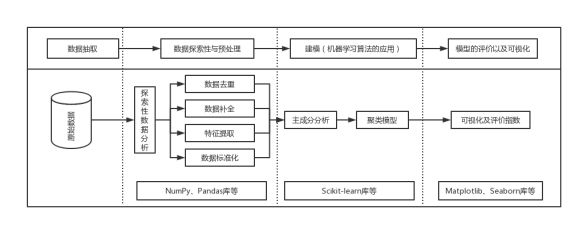
针对目标1采用如下图所示的流程图进行处理:

1. 数据探索性与预处理

   1. 合并文件并检查缺失值

      import pandas as pd
      # 读取三个Excel文件
      df1 = pd.read_excel('附件1第一年三餐消费数据.xlsx')
      df2 = pd.read_excel('附件2第二年三餐消费数据.xlsx')
      df3 = pd.read_excel('附件3第三年三餐消费数据.xlsx')
      # 合并三个 DataFrame 对象
      df_all = pd.concat([df1, df2, df3], ignore_index=True)
      # 按序号分组，求和
      result = df_all.groupby(['序号']).sum()
      # 重置索引
      result = result.reset_index()
      # 将结果输出到新文件
      result.to_excel('firstSum.xlsx', index=False)
      # 检查缺失值
      print(result.isnull().sum())

      2.计算文件的当中的值

   2. import pandas as pd
      # 读取 Excel 文件
      df = pd.read_excel('firstSum.xlsx', header=0)
      # 排序（按照序号升序）
      df = df.sort_values(by=['序号'])
      # 计算每行的消费信息
      consumption_data = []
      for idx, row in df.iterrows():
          data = list(row[1:])
          count = data.count(0)
          data = [val for val in data if val != 0]
          consumption_data.append({
              '序号': row['序号'],
              'max': max(data) if len(data) > 0 else '',
              'min': min(data) if len(data) > 0 else '',
              'median': pd.Series(data).median() if len(data) > 0 else '',
              'mean': pd.Series(data).mean() if len(data) > 0 else '',
              'variance': pd.Series(data).var(ddof=0) if len(data) > 0 else '',
              'count': len(data),
              'unconsumed': count
          })
      # 将结果写入新的 Excel 文件
      wb = pd.ExcelWriter('ClearfirstSum.xlsx')
      pd.DataFrame(consumption_data).to_excel(wb, index=False)
      wb.save()

      使用了pandas库来读取一个名为'firstSum.xlsx'的Excel文件，并对数据进行处理和计算，然后将结果写入一个新的Excel文件'ClearfirstSum.xlsx'。在新的Excel文件中，每行数据包含了原始数据中的序号以及对应的最大值、最小值、中位数、平均值、方差、有效值的数量和未消费的数量。同时采用EXCEL中VLOOKUP函数关联男女性别信息。

消费指数的描述性分析

1. 根据ClearfirstSum.xlsx中的数据，首先对男女生的情况进行分别统计，如下表所示

   性别	max	min	median	mean	variance	count	unconsumed
   女	5579.683	94.869	860.250	1036.128	584478.327	657.196	2636.804
   男	6004.395	108.813	1106.591	1261.450	641095.596	818.079	2475.921

   通过对比数据，可以发现男性学生的平均、中位数消费金额均高于女性学生，但是方差也更大，说明男生的消费差异更大。此外，女性学生未消费的人数较多。

2. 1. 1. 利用平均消费指数进行聚类

         1. 首先对数据进行标准化处理

 1.公式为：（X-min）/ （max-min）

2.作用：对原始数据的线性变换，使结果落到[0,1]区间。

1. 1. 1. 1. 其次对数据进行截尾处理

样本数据足够多时为了剔除一些极端值对研究的影响，一般会对连续变量进行缩尾/截尾处理。会在从小到大排列后，处理超出变量特定百分位范围的数值，标准为低于下限和超出上限。截尾是直接删除值，处理范围为上限99%，下限1%。

此步骤直接使用Excel进行处理，到的文件origindata.Xlsx

1. 1. 1. 1. 进行聚类模型的个数的选择

2. 1. 1. 1. 进行聚类模型的算法的处理

利用spsspro利用肘部法则得出聚类数对比图，该图用于选择较好的聚类数量，横坐标是聚类个数，纵坐标是K均值聚类的损失函数是所有样本到类别中心的距离平方和，也就是误差平方和（值越小说明聚类效果越好）。可以通过“坡度趋于平缓”的找出最佳的类簇数量，如图所示确定个数3最为合适。

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score, davies_bouldin_score, calinski_harabasz_score

# 读取Excel文件
data = pd.read_excel('origindata.xlsx')
# 提取"mean_min-max"标准化列数据
normalized_data = data['mean_min-max标准化'].values.reshape(-1, 1)
# 使用K均值聚类将数据分为3个簇
kmeans = KMeans(n_clusters=3)
kmeans.fit(normalized_data)
# 获取每个数据点的簇索引
cluster_labels = kmeans.labels_
# 计算轮廓系数、DBI和CH指数
silhouette_avg = silhouette_score(normalized_data, cluster_labels)
dbi_score = davies_bouldin_score(normalized_data, cluster_labels)
ch_score = calinski_harabasz_score(normalized_data, cluster_labels)
# 将簇索引和轮廓系数添加到数据框中
data['Cluster'] = cluster_labels
# 生成新的Excel文件
data.to_excel('newdata.xlsx', index_label='Index')
# 绘制散点图
plt.scatter(data.index, normalized_data, c=cluster_labels, cmap='viridis')
plt.title('Clustered Data')
plt.xlabel('Index')
plt.ylabel('mean_min-max')
plt.show()
# 显示轮廓系数、DBI和CH指数
print('Silhouette Score:', silhouette_avg)
print('DBI Score:', dbi_score)
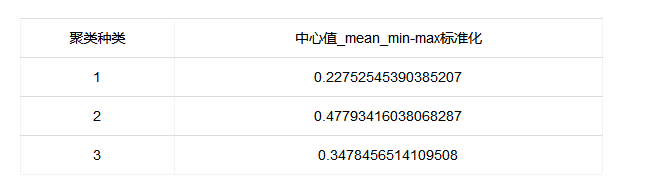
print('CH Score:', ch_score)

 

有三个聚类种类，它们的中心值经过标准化后分别为0.2275、0.4779和0.3478。这些数值反映了不同聚类种类在特定属性上的相对位置。

1. 1. 1. 聚类模型的评价

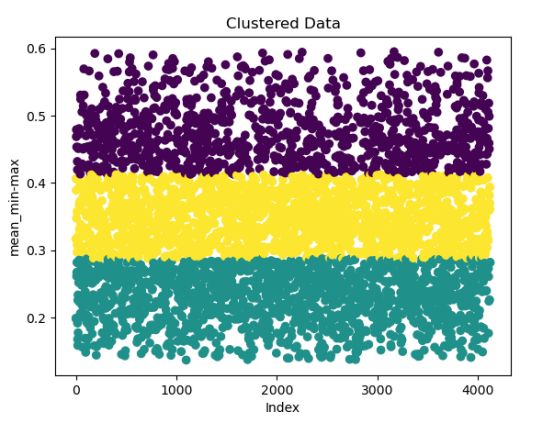
绘制数据的散点图：

运行结果：

Silhouette Score: 0.5653847645608842

DBI Score: 0.5230993540053457

CH Score: 12460.820513494542

总结：

聚类模型的轮廓系数为0.565，DBI（Davies-Bouldin Index）为0.523，CH（Calinski-Harabasz）为12460.821。

轮廓系数用于评估聚类结果的紧密性和分离度，取值范围为[-1,1]，数值越接近1表示聚类结果越好。DBI用于衡量簇内的紧密度和簇间的分离度，数值越小表示聚类效果越好。CH指标是一种聚类有效性指标，用于评估聚类结果的质量。数值越大表示聚类结果越好。

综合这三个指标来看，轮廓系数为0.565表示聚类结果相对一致，DBI为0.523说明簇内紧密度较高且簇间分离度较好，而CH为12460.821表示聚类结果的质量较高。

1. 1. 1. 聚类模型的结果关联

import pandas as pd
# 读取Excel文件
data = pd.read_excel('newdata.xlsx')
# 利用Cluster的值进行贫困等级分类
data['Poverty Level'] = data['Cluster'].map({0: '特别贫困', 1: '一般贫困', 2: '不贫困'})
# 生成新的Excel文件
data.to_excel('level.xlsx', index=False)
# 打印结果
print(data[['Index', 'Cluster', 'Poverty Level']])

运行结果：

1. 1. 利用决策树模型进行预测

附件8给出部分同学第一学年后经其他方式认定的贫困程度等级（粗粒度），补全最大值，最小值，中位数，平均值，标准差，方差，以及消费次数这些信息，利用机器学习算法中的决策树建立数学模型，依据消费行为进行模型训练，预测贫困程度，补全附件9。通过2019sum.xlsx、2020sum.xlsx、2021sum.xlsx三个数据文件，可以进一步结合第1问研究结论预测该组同学第二、第三学年的贫困程度隐形认定等级，并且分析相关变化[4]。

首先，定义树上的每个节点 j对应的特征为 x(j)∈Rmx(j)∈Rm，对应的阈值为 tj。定义一个节点 j的两个子节点分别为左子树和右子树，则对于一个输入样本 x，我们可以从根节点开始按照以下规则一直往下走：

1. 当 x(j)≤tjx(j)≤tj​ 时，选择左子树；
2. 当 x(j)>tjx(j)>tj​ 时，选择右子树；
3. 直到到达某个叶子节点为止。

假设表示节点j对应的预测类别，则有：

 其中 L是所有叶子节点的个数，是第个叶子节点所代表的样本区域，I是指示函数，当括号中的条件成立时，取值为1，否则取值为0。

1. 1. 决策数模型的数据处理

文件中贫困程度2是特别困难，1是一般困难，0是不困难

根据前面的已经得到的level.xlsx文件中的信息关联附件8和9，补全序号、贫困程度、max_min-max标准化、min_min-max标准化、median_min-max标准化、mean_min-max标准化、variance_min-max标准化、count_min-max标准化从而进行机器学习算法

1. 1. 决策树模型的参数设置

模型参数如下表：

 

特征重要性：

 

决策树算法思想

import pandas as pd
from sklearn.tree import DecisionTreeRegressor
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score

# 读取附件8中的标签信息贫困程度.xlsx
labels_data = pd.read_excel('附件8 已知贫困标签.xlsx')
labels = labels_data['贫困程度']

# 读取附件9中的待补全标签数据.xlsx
incomplete_data = pd.read_excel('附件9 问题2待补全标签数据.xlsx')

# 使用MinMaxScaler进行数据的归一化处理
scaler = MinMaxScaler()
normalized_labels = scaler.fit_transform(labels.values.reshape(-1, 1))

# 特征选择，这里选择了 "max_min-max标准化"、"min_min-max标准化"、"median_min-max标准化"、"mean_min-max标准化"、"variance_min-max标准化" 和 "count_min-max标准化"
features = labels_data[['max_min-max标准化', 'min_min-max标准化', 'median_min-max标准化', 'mean_min-max标准化', 'variance_min-max标准化', 'count_min-max标准化']]

# 将数据分割为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(features, normalized_labels, test_size=0.3, random_state=42)

# 创建决策树回归模型并进行训练
model = DecisionTreeRegressor()
model.fit(X_train, y_train)

# 在测试集上进行预测
predicted_labels = model.predict(X_test)

# 反归一化得到原始贫困程度的预测值
predicted_labels = scaler.inverse_transform(predicted_labels.reshape(-1, 1))

# 计算评估指标
accuracy = accuracy_score(scaler.inverse_transform(y_test), predicted_labels)
recall = recall_score(scaler.inverse_transform(y_test), predicted_labels, average='macro')
precision = precision_score(scaler.inverse_transform(y_test), predicted_labels, average='macro')
f1 = f1_score(scaler.inverse_transform(y_test), predicted_labels, average='macro')

print("准确率:", accuracy)
print("召回率:", recall)
print("精确率:", precision)
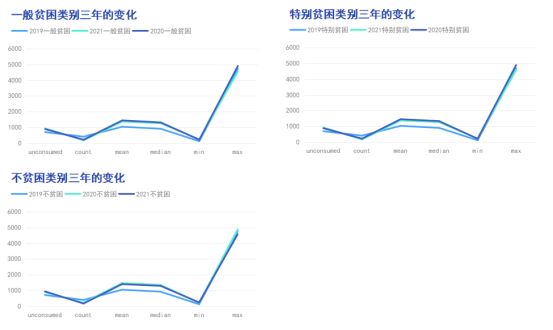
print("F1值:", f1)

• 结果的分析
  1. 定量分析该群体三学年的主要消费行为特征变化规律

 

可以观察到一般贫困学生类别在不同年份的变化情况如下：

1. 未消费数量：从2019年的695逐渐增加到2021年的933，然后在2020年略微减少到886。这表明一般贫困学生中未进行消费的人数整体上呈现出一定的波动。
2. 消费次数总和：从2019年的403逐渐降低到2021年的165，然后在2020年有所增加到212。这意味着一般贫困学生的消费次数总和整体上呈现出下降的趋势，但在2020年有所反弹。
3. 平均消费金额：从2019年的1033.80逐渐增加到2021年的1364.66，然后在2020年又有所增加到1438.51。这说明一般贫困学生的平均消费金额整体上有所增加，并且在2020年达到了一个相对较高的水平。
4. 消费金额中位数：从2019年的906.48逐渐增加到2021年的1258.17，然后在2020年再次有所增加到1308.78。这表明一般贫困学生的消费金额中位数整体上呈现逐年增长的趋势。
5. 一般贫困学生类别在不同年份的最小消费金额和最大消费金额有所变化。最小消费金额在2019年到2020年之间有较大的增长，而最大消费金额在同一时间段内有一定的增长；然而，在2020年到2021年之间，最大消费金额有所降低。

综合来看，一般贫困学生类别在这几年的变化情况显示出未消费数量波动、消费次数总和下降、平均消费金额上升以及消费金额中位数逐年增长的趋势。这些变化可能受到多种因素的影响，例如经济情况、学生消费行为变化等。

根据提供的数据，特别贫困学生类别在不同年份的消费主要变化情况如下：

1. 未消费数量：2019年特别贫困学生中有690人未进行消费，2020年增加到880人，2021年进一步增加到931人。这表示在过去三年中，特别贫困学生中没有进行消费的人数有所增加。
2. 消费次数总和：2019年特别贫困学生的消费次数总和为408次，2020年略有增加至218次，但在2021年减少至167次。这表明特别贫困学生在消费方面存在一定的波动。
3. 平均消费金额：2019年特别贫困学生的平均消费金额为1032.03元，2020年增加至1454.00元，再在2021年略微增加至1374.23元。可见，在过去三年中，特别贫困学生的平均消费金额有所上升。
4. 消费金额中位数：在特别贫困学生群体中，消费金额的中位数可以反映整体消费水平。从数据中可以看出，2019年的消费金额中位数为902.52元，2020年增加至1335.31元，而2021年的中位数为1270.12元。这表明特别贫困学生的消费金额中位数呈现出一定的波动。
5. 最小消费金额和最大消费金额：特别贫困学生的最小消费金额和最大消费金额也发生了变化。最小消费金额从2019年的117.12元上升至2020年的210.20元，并在2021年进一步上升至226.79元。然而，最大消费金额在2020年有所增加（4900.54元），但在2021年略有下降（4588.06元）。

根据提供的数据，我们可以观察到不贫困学生在未消费数量、消费次数总和、平均消费金额、消费金额中位数以及最小和最大消费金额方面发生了以下变化：

1. 未消费数量：2019年不贫困学生中有704人未进行消费，2020年增加到886人，2021年进一步增加到936人。这表明在过去三年中，不贫困学生中未进行消费的人数有所增加。
2. 消费次数总和：2019年不贫困学生的消费次数总和为394次，2020年减少至212次，2021年进一步下降至162次。这表明不贫困学生的消费次数总和在过去三年中呈下降趋势。
3. 平均消费金额：2019年不贫困学生的平均消费金额为1043.91元，2020年增加至1463.69元，2021年略有下降至1398.04元。可见，不贫困学生的平均消费金额存在一定的波动。
4. 消费金额中位数：在不贫困学生群体中，消费金额的中位数可以反映整体消费水平。从数据中可以看出，2019年的消费金额中位数为917.12元，2020年增加至1349.46元，而2021年的中位数为1287.89元。这表明不贫困学生的消费金额中位数呈现出一定的波动。
5. 最小和最大消费金额：不贫困学生的最小消费金额从2019年的117.66元上升至2020年的207.64元，并在2021年进一步上升至230.62元。然而，最大消费金额在2020年有所增加（4880.77元），但在2021年略有下降（4569.30元）。
   1. 根据附件1-3消费行为预测贫困程度

根据决策树得出以下结果：

其中一般贫困为53、240、768、1081、1422、1494、1836、2099、2103、2527、2889、2972、3155、3247、3346、3353、3356、3694、3710、3870、4068共计21名同学，特别贫困1043、1613名同学。

1. 1. 模型评价

   2. 

根据提供的数据，您给出了分类模型在训练集和测试集上的准确率、召回率、精确率和F1值。下面是对这些指标的解释：

准确率（Accuracy）：分类正确的样本数占总样本数的比例。即对于所有预测结果中正确的样本数与总样本数的比值。训练集的准确率为0.792，测试集的准确率为0.721。

召回率（Recall）：在所有真实正例中被正确预测为正例的比例。即真实正例中被正确预测为正例的样本数与真实正例的样本数的比值。训练集的召回率为0.792，测试集的召回率为0.721。

精确率（Precision）：在所有被预测为正例的样本中，确实为正例的比例。即被正确预测为正例的样本数与所有被预测为正例的样本数的比值。训练集的精确率为0.803，测试集的精确率为0.571。

F1值：综合考虑了精确率和召回率的指标，是精确率和召回率的调和平均值。F1值可以评估分类器的综合性能，当精确率和召回率同时较高时，F1值也会较高。训练集的F1值为0.723，测试集的F1值为0.628。

其中，训练集和测试集的准确率和召回率比较接近，说明模型在两个数据集上的表现相对一致。但是精确率和F1值在测试集上相对较低，说明模型在预测正例时存在一定程度的误判。需要进一步分析模型的预测结果，并可能采取一些调整或优化措施来提高模型的性能。

gitee代码以及数据文件

小蒋同学的CSDN: 用于CSDN文章中的代码分享 - Gitee.com