【论文阅读】Graphs-at-a-time: Query Language and Access Methods for Graph Databases

He H, Singh A K. Graphs-at-a-time: query language and access methods for graph databases[C]//Proceedings of the 2008 ACM SIGMOD international conference on Management of data. 2008: 405-418.

ABSTRACT

随着图数据在各种领域中的流行，人们越来越需要一种语言来查询和操作具有异构属性和结构的图。我们提出了一种图形数据库的查询语言，它支持节点、边和图形上的任意属性。在这种语言中，图是信息的基本单位，每个查询都操作一个或多个图的集合。为了允许图结构的灵活组合，我们将形式化语言的概念从字符串扩展到图域。给出了由关系代数扩展而来的图代数，其中将选择算子推广到图模式匹配，并引入了重写匹配图的组合算子。然后，我们研究了选择算子的访问方法。由于子图同构的np完备性，在大图上的模式匹配具有挑战性。我们通过结合各种技术来解决这个问题：使用邻域子图和轮廓，联合缩减搜索空间，以及优化搜索顺序。在真实的和合成的大图上的实验结果表明，我们的图特定的优化比基于sql的实现要高出多个数量级。

1. INTRODUCTION

多个领域中的数据可以自然地建模为图。例如：语义Web [28]、GIS、图像[2]、视频[20]、社交网络、生物信息学和化学信息学。语义Web将Web上的信息标准化为具有一组实体和显式关系的图。在生物信息学中，图表代表了几种信息：蛋白质结构可以被建模为一组残基（节点）及其空间邻近性（边）；蛋白质相互作用网络可以通过一组基因/蛋白质（节点）和物理相互作用（边）来类似地建模。在化学信息学中，图表被用来表示化合物中的原子和键。
上述数据日益增长的异构性和规模，激发了人们对以图形数据为中心的各种应用程序的兴趣。现有的数据模型、查询语言和数据库系统都不能为这些数据的建模、管理和查询提供足够的支持。开发基于图形的本地数据管理系统有许多原因。考虑查询的表达性：我们需要在其完全通用性中操作图形的查询语言。这意味着能够在节点和边上定义约束（图结构和值），而不是以一次迭代的方式，而是同时对整个感兴趣的对象。这也意味着能够返回一个图（或一组图）作为结果，而不仅仅是一组节点。对本地图形数据库的另一个需求是出于效率方面的考虑。有一些启发式技术和索引技术只能在我们在图形的领域中操作时才能应用。

1.1 Graphs-at-a-time Queries

抽象地说，图形查询将图形模式作为输入，从数据库中检索包含（或类似于）查询模式的图形，并返回检索到的图形或由检索到的图形组成的新图形。图形查询的示例可以在各种领域中找到：

• 找到所有包含一个给定的芳香环和一个侧链的杂环化合物。环和侧链都被指定为图，原子为节点，键为边。
• 找到所有包含α-β-bubel基序[4]的蛋白质结构。这个基序被指定为由另一个α螺旋循环所包含的β链循环。
• 给定一个来自一个物种的查询蛋白复合物，它在另一个物种中是否功能保守？
  蛋白质复合体可以被指定为一个由基因本体论[12]术语标记的节点（蛋白质）的图。
• 从一个RDF（资源描述框架[22]）图中找到所有实例，其中一个公司的两个部门共享同一个航运公司。查询图（由三个节点和两条边组成）具有以下约束条件，即节点共享相同的公司属性，并且这些边由一个“运输”属性标记。将结果报告为单个图，其中部门为节点，以及共享托运人的节点之间的边。
• 在指定的会议论文集集中找到DBLP数据集（以小图表示的论文集合）中的所有合著者。将结果作为合作作者图报告结果。
  如上文所示，人们越来越需要一种语言来查询和操作具有异构属性和结构的图。该语言应该是图形的原生语言，足够通用，足以满足真实世界数据的异构性质，声明性，但可实现。最重要的是，图形查询语言需要支持以下特性。
  图应该是信息的基本单位。该语言应该显式地处理图形，而查询应该是一次图形，将一个或多个图形集合作为输入，并生成一组图形集合作为输出。

1.2 Graph Specific Optimizations

图形查询语言只有在能够有效地实现的情况下才有用。这一点特别重要，因为人们会遇到子图同构的常见瓶颈。由于图是关系的特殊情况，所以图的查询仍然可以简化为关系模型。然而，通用关系模型很少允许进行特定于图的优化，因为它将图的结构分解为单独的关系。让我们考虑下面一个简单的例子。图1显示了一个图查询和一个图，其中每个节点都有一个单一的标签作为其属性（具有相同标签的节点通过下标进行区分）。

一个基于sql的实现将把图存储在两个表中。表V（vid，标签）存储了节点1的集合，其中vid是节点标识符。表E（vid1，vid2）存储了一组边，其中vid1和vid2是每个边的端点。然后，图形查询可以通过多个连接来实现：



从上面的示例中可以看出，图结构的全局视图在SQL查询中丢失了。这可以防止对利用局部或全局图结构信息的搜索空间的修剪。例如，G中的节点A2和C1可以安全地修剪，因为它们只有一个邻居。节点B2也可以在A2被修剪后进行修剪。此外，SQL查询还涉及到许多连接操作。传统的查询优化技术，如动态规划，不能很好地扩展到连接的数量。这使得基于sql的实现效率低下。

1.3 Our Approach

在本文中，我们提出了一种使用图形模式作为基本操作单元的图形查询语言GraphQL。图模式由图结构和基于图的属性的谓词组成。为了允许对图形结构进行灵活的操作（对于定义图形查询和数据库图形都很有用），我们引入了图形的形式化语言的概念。GraphQL的核心是一个图代数，其中将选择算子推广到图模式匹配，并引入了一个组合算子来重写匹配的图。就表达能力而言，GraphQL是关系完整的，并包含在数据日志[24]中。GraphQL的非递归版本等价于关系代数。
在本文的第二部分中，我们考虑了对图查询的评估。选择操作符的访问方法原来是主要的挑战，特别是当图很大时。我们利用三种利用图结构信息的技术来加速基本的图模式匹配算法。首先，我们使用邻域子图或其轮廓来生成具有局部剪枝的搜索空间。其次，我们利用全局结构信息同时减少了整体搜索空间。第三，我们基于一个为图设计的成本模型来优化搜索顺序。正如我们在实验结果中所展示的那样，这三种技术的结合允许我们同时扩展到大型查询和大型图。
我们的工作有以下贡献：
1.我们引入了图的形式化语言的概念。它对于操作图形很有用，也是我们的查询语言的基础（第2节）。
2.我们提出了GraphQL查询语言。这种语言支持图形作为信息、任意属性和面向集合的操作的基本单元（第3节）。
3.我们沿着关系代数的线定义了一个图代数。图代数将选择算子推广到图模式匹配，并引入了一个重写匹配图的组合算子。在表达能力方面，我们证明了图代数是关系完备的，并且包含在数据日志（第3.3节）中。
4.我们提出了对大图上的选择算子的有效访问方法。在大型实图和合成图上的实验结果表明，我们的图特定优化比基于sql的实现优出一个数量级（第4节和第5节）。

2. FORMAL LANGUAGE FOR GRAPHS

在本节中，我们将介绍图的形式化语言的概念。这个概念对于组合和操作图形结构很有用。它是我们的图形查询语言的基础。
在经典的形式化语言[17]中，形式化语法由有限的终端和非终端集以及生成字符串的有限的生产规则集组成。我们将形式语法的概念从字符串扩展到图域，其中基本的操作单元是一个图结构，即图主题。一个图主题可以是一个简单的图，也可以通过连接、分离和重复由其他图主题组成。图语法是一个有限的图主题集。图语法的语言是由该语法的图图案推导出的所有图的集合。

2.1 Simple Graph Motifs

一个简单的图的主题是一个正规的图。它由一组节点和一组边组成。每个节点、边或图都由一个变量来标识。如果没有在其他地方被引用，则可以省略该变量名。节点和边对应于终端，而图对应于非终端。
每个节点、边或图都可以具有多个属性。图3(a)显示了一个简单的图形主题及其图形表示。

2.2 Complex Graph Motifs

一个图形图案可以由其他的图形图案组成。在现有的语法中，一个字符串是通过串联、分离或重复使用其他字符串来获得的。一个字符串通过它的头和尾连接到其他字符串，这是隐式指定的。然而，在图域中，一个图可以通过任意节点连接到其他图。因此，我们需要显式地指定这些互连。

2.2.1 Concatenation

一个图形主题可以由两个或多个图形主题组成。组成的主题可以不连接，也可以以两种方式之一连接。一种方法是通过新的边来连接每个主题中的节点。图3(b)显示了一个按边连接的示例。图主题G2由图3(a).中的两个主题G1组成这两个图案由两条边连接起来。为了避免名称冲突，我们使用关键字“as”引入了别名。
另一种连接方式是统一每个主题中的节点。如果两条边各自的端节点统一，则它们将自动统一。图3©显示了一个通过统一进行连接的示例。
图形主题的成员是指在该主题的主体中声明的一个节点、一条边或一个图形主题。如果图形主题的主体或派生主体包含自己作为成员，则它是递归的。成员变量从声明的范围和任何嵌套的范围中都可见。在其他范围中声明的变量可以通过它们的封闭图变量进行引用。

2.2.2 Disjunction

一个图形主题可以定义为两个或多个图形主题的分离。图3(d)显示了分离的一个例子。在图形主题G4中，有两个匿名的图形主题被声明（由节点v3或节点v3和v4组成）。其中只有一个被选中并连接到G4的其余部分。所有的图形图案应该有相同的“界面”。

2.2.3 Repetition (Kleene Star)

在现有的形式语法中，重复的形式为S→S1∗。它也可以写成S→S1S | ε。我们通过这种自递归来指定图形图案的重复。图3(e)显示了一个路径和一个循环的构造。在基本情况下，路径有两个节点和一条边。在递归步骤中，路径将自己作为成员包含，添加一个新节点v1，该节点连接到嵌套路径的v1，并导出嵌套v2，使新路径具有相同的“接口”。关键字“导出”等价于声明一个新节点并将其与嵌套节点统一。图主题循环由主题路径和一条连接路径的末端节点的附加边组成。
GraphQL中的递归并不局限于路径和循环。图3(f)展示了一个例子，其中重复单元是一个图的主题。主题G5包含任意数量的主题G1和一个根节点v0。该声明递归地包含G5本身和一个新的G1，其中包含G1。v1连接到v0，其中v0从嵌套的G5导出。第一个结果图由节点v0单独组成，第二个节点v0通过边e1连接到G1，第三个节点v0通过边e1连接到G1的两个实例组成，以此类推。

3. GRAPH QUERY LANGUAGE

在本节中，我们将描述图形查询语言。我们首先描述了这个数据模型。接下来，我们定义一个图形模式，它是图形查询的主要构建块。然后，我们为查询语言定义了一个图代数，并研究了其表达能力。最后，我们通过一个例子来说明图的查询语法。

3.1 Data Model

在GraphQL数据模型中，每个节点、边或图都可以具有任意属性。我们使用一个元组，一个名称和值对的列表，来表示这些属性。该元组可以有一个可选的标记，它表示该元组的类型。图4显示了一个表示一篇论文（节点是未连接的）的示例图。节点v1有两个属性“标题”和“年份”。节点v2和v3有一个标签“作者”和一个属性“name”。

在关系模型中，元组是信息的基本单元。每个关系代数运算符操作元组的集合。在GraphQL中，图是信息的基本单位。每个操作符将一个或多个图形集合作为输入，并生成一组图形集合作为输出。这类似于TAX模型[18]，其中树是基本单元，操作员处理树的集合。图形数据库由一个或多个集合组成的图。集合中的图不一定具有相同的结构和属性。但是，它们仍然可以通过坚持一个图形模式来以统一的方式处理它们。

3.2 Graph Patterns

本质上，图模式是一个图主题加上一个对主题属性的谓词。图形模式用于选择感兴趣的图形。它是图形查询的主要构建块。
定义1。（图模式）图形模式是一对P =（M，F），其中M是一个图形主题，F是基于该主题属性的谓词。
谓词F可以是布尔表达式或算术比较表达式的组合。图5显示了一个示例图模式。谓词可以分解为单个节点或边上的谓词，如图右侧所示。

接下来，我们定义了图模式匹配的概念，它将子图的同构推广到谓词的计算中。
定义2。（图模式匹配）如果存在一个内射映射φ： V (M)→V (G)，这样(i)对于∀（u，V），∈E (M)，（φ(u)，φ(v)）是G中的一条边，并且ii)谓词Fφ(G)成立。

图6显示了图5中的模式与图4中的图形之间的图形模式匹配的一个示例。
一旦图形模式与图形匹配，它们之间的绑定就可以用于访问图形。这允许人们统一地访问图的集合，即使它们可能具有异构的结构和属性。我们使用一个匹配的图来表示图模式和图之间的绑定。
定义3。（匹配图）给定模式P和图G之间的内射映射φ，匹配图是一个三%φPG&，用φP (G)表示。
虽然形式上是三重图，但匹配的图具有图的所有特征。因此，所有适用于一个图也适用于匹配的图，例如，匹配的图的集合也是图的集合。
一个图形模式可以在多个地方匹配一个图形，从而产生多个绑定（匹配的图）。当我们在第3.3.1节中讨论选择操作符时，我们将进一步考虑这一点。

3.3 Graph Algebra

我们沿着关系代数的线定义了一个图代数。然而，有两个重要的区别。首先，将选择算子推广到图模式匹配。其次，引入一个组合算子，从匹配的图中生成新的图。

3.3.1 Selection

选择操作符σ是使用图形模式p来定义的。它将一组图形C作为输入，并生成一组与图形模式相匹配的图形，用σP ©表示。
一个图形模式可以多次匹配一个图形。因此，一个选择可以为每个图返回许多实例。我们使用一个“详尽的”选项来指定它是否应该从图形模式返回到图形的一个或所有可能的映射。是否需要一个或所有的映射取决于应用程序。输出的是一组匹配的图表：

3.3.2 Cartesian Product and Join

一个笛卡尔积算子取两个图C和图D的集合，并生成一组图作为输出。每个输出图都由一个来自C的图和另一个来自d的图组成。组成图是不连通的：

连接算子可以由一个笛卡尔积来定义，然后是一个选择： C &‘ P D = σP（C×D）。
在值连接中，连接条件是组成图属性的谓词，例如“G1.name=G2.name.”在结构连接中，组成图可以通过边或统一来连接。这是使用下面将描述的组合运算符来指定的。

3.3.3 Composition

该组合运算符通过组合从匹配的图中获得的信息来生成新的图。我们首先定义指定图形的输出结构的图形模板，然后定义组合操作符。
定义4。（图形模板）图形模板T由一个作为图形模式的形式参数列表和一个通过使用图形模式中的变量来定义图形的模板体组成。
一旦给出了实际的参数（匹配的图），一个图模板就会被实例化为一个真实的图。这类似于对函数的调用：模板主体是函数体；图形模式是形式化的参数；匹配的图是实际的参数。所得到的图可以用TP1… Pk（G1，…，Gk）来表示。
图7显示了一个示例图模板TP和一个实例化的图TP (G)。P是的的形式参数样板模板体由由P构造的两个节点和它们之间的一条边组成。给定实际的参数G，该模板被实例化为一个图。

使用具有单个参数的图模板TP定义了基本组合操作符ω。它将一组匹配的图C作为输入，并生成一组图作为输出：

通常，组合操作符可能允许两个或多个图形集合作为输入。这可以用一个原始组合算子和笛卡尔积算子来表示：

投影和重命名，关系代数的另外两个算子，可以用组合算子来表示。集合运算符（并集、差集、交集）也可以很容易地定义。在表达能力方面，这五个运算符（选择、笛卡尔积、原始组成、并集和差分）都是完整的。
代数定律对查询优化非常重要。由于我们的图代数是沿着关系代数的线来定义的，所以关系代数的定律仍然存在。

3.4 FLWR Expressions

我们采用XQuery [3]中的FLWR（For、Lere、和Retvern）表达式作为图查询语言的语法。由于已经定义了一个图代数，所以为了简洁，我们跳过了查询语法。

图8显示了一个从论文集合中生成合作作者图C的示例。该查询声明，论文中的任何一对作者都应该出现在共同作者图中，并且它们之间有一条边。
图模式P匹配了一篇论文中的两位作者。for子句从数据源中选择所有此类对。let子句将每一对放在合作作者图中，并在它们之间添加一条边。统一确保每个作者只出现一次。同样，如果两条边的端节点是统一的，那么它们就会自动统一。
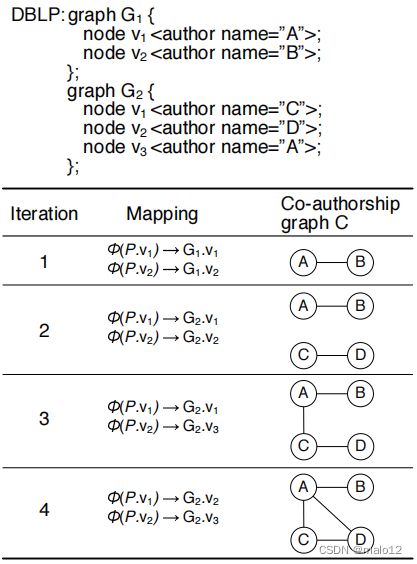
图9显示了该查询的一个正在运行的示例。DBLP集合由两个图G1和G2组成。首先选择一对作者节点（A、B），并在它们之间插入一条边。接下来选择该对（C、D），并插入（C、D）子图。当选择第三对（A，C）时，统一确保旧节点被重用，并且在现有的A和C之间添加一条边。第四对的处理再添加一条边并完成执行。

查询可以转换为递归代数表达式：

其中，σP（“DBLP”）对应于for子句，τP，C是let子句中的图模板，J是连接条件的图模式：P.v1。name= C.v1.name & P.v2.name = C.v2.name.代数表达式是一个结构连接，它由三个原语算子组成：笛卡尔积、原语组成和选择。

3.5 Expressive Power

我们首先证明了关系代数（RA）包含在GraphQL中。
定理1。（RA⊆GraphQL）对于任何RA表达式，都存在一个等价的GraphQL代数表达式。
证明。我们可以在GraphQL中表示一个关系（元组），该图有一个节点作为属性元组。RA的原始操作（选择、投影、笛卡尔积、并集、差分）然后可以在GraphQL中表示。选择运算符可以使用以给定谓词作为选择条件的图模式来模拟选择。对于投影，可以使用组合操作符将投影属性重写到新节点。其他操作（产品、联合、差异）也很简单。
接下来，我们将展示GraphQL包含在数据日志中。通过将图形、图形模式和图形模板转换为数据日志的事实和规则，证明了这一点。
定理2。（GraphQL⊆数据日志）对于任何GraphQL代数表达式，都存在一个等价的数据日志程序。
证明。我们首先将数据库的所有图形转换为数据日志的事实。图10显示了一个翻译的示例。本质上，我们将图中的每个变量重写为一个唯一的常数字符串，然后在图与每个节点和边之间建立一个连接。注意，对于无向图，我们需要写一条边两次来排列它的结束节点。

对于每个图形模式，我们将其转换为数据日志的规则。图11给出了这种翻译的一个例子。规则的主体是图形模式的组成元素的连接。图模式的谓词是很自然地编写出来的。当且仅当相应的规则与表示图形的事实匹配时，就可以证明图形模式与图形匹配。
随后，人们可以将图的代数操作转换为数据日志，其方式类似于将RA转换为数据日志。因此，我们可以将任何GraphQL代数表达式转换为一个等价的数据日志程序。

众所周知，非递归Datalog（nr-Datalog）等价于RA。因此，GraphQL的非递归版本（nr-GraphQL）也等同于RA。
推论1. nr-GraphQL≡RA。

4. ACCESS METHODS

在本节中，我们将讨论选择操作符的访问方法，即给定一个图形模式和一组图形，如何生成一个匹配的图形集合。
通常，一个图形数据库可以分为两类。其中一类是大量的小图表的集合，例如，化合物。这一类人面临的主要挑战是减少成对图模式匹配的数量。许多图索引技术已经被提出来解决这一挑战[15,29,35]。
在第二类中，图数据库由一些非常大的图组成，例如，蛋白质交互网络、网络信息、社会网络。这里的挑战是加速图形模式本身的匹配。在本文中，我们重点研究了大型图的访问方法。然而，所提出的方法也适用于小图。
我们首先在第4.1节中描述了基本的图形模式匹配算法，然后在第4.2、4.3和4.4节中讨论了对基本算法的加速度。我们将注意力限制在非递归图模式和内存内处理上。

4.1 Graph Pattern Matching

图模式匹配以图模式P和图G作为输入，并产生一个或所有可行的映射作为输出。它被用作选择操作符的子例程。算法1概述了基本的算法。
图模式P的谓词被重写为对单个节点Fu和边Fe的谓词。不能向下推的谓词，例如u1.label=u2.label，仍然作为图宽的谓词f。我们将节点u的可行伙伴定义如下。
定义5。（可行的配偶）节点u的可行的配偶Φ(u)是图G中满足谓词Fu的节点集：

该算法分为两个阶段。第一阶段（第1-4行）检索模式中每个节点u的可行配对。得到的产品Φ（u1）×…×Φ（uk）形成了搜索空间，算法的第二阶段（第7-26行）在上面搜索子图同构。
定义6。（搜索空间）图模式匹配的搜索空间被定义为图模式的每个节点的可行配偶的乘积：Φ（u1）×…×Φ（uk），其中k是图模式的大小。
第二阶段（第7-27行）以深度优先的方式搜索图形模式和图形之间的匹配。过程搜索(i)在第i个节点上进行迭代，以找到该节点的可行映射。过程检查（ui，v）检查ui是否可以通过考虑它们的边来映射到v。第12行将ui映射到v。第13-16行继续搜索下一个节点，或者如果它是最后一个节点，则计算图范围的谓词。如果它是真的，那么已经找到了一个可行的映射φ： V §→V (G)并被报告了（第15行）。如果只需要一个映射，则第16行将立即停止搜索。
图模式和图分别表示为顶点集和边集。此外，图模式的邻接列表被用于支持第21行。对于第22行，图G的边可以用散列表表示，其中键是端点对。避免重复计算边谓词（第22行），另一个对话表可用于存储计算的边对。
算法1的最坏情况下的时间复杂度为O（nk），其中n和k分别为图G和图模式P的大小。这种复杂性是已知的np困难的子图同构的结果。在实践中，运行时间取决于搜索空间的大小。接下来，我们将讨论通过减少这个搜索空间并以最佳顺序探索它来加速算法1的可能方法。
1.如何减少每个节点ui的Φ（ui）的大小？如何有效地检索Φ（ui）？
2.如何减少整体搜索空间Φ（u1）×…×Φ（uk）？
3.如何优化搜索顺序？

我们提出了三种技术，分别解决了上述问题。第一种技术分别删除每个Φ（ui），并通过索引有效地检索它。第二种技术通过同时考虑模式中的所有节点来修剪整个搜索空间。第三种技术应用传统的查询优化的思想来找到正确的搜索顺序。

4.2 Local Pruning and Retrieval of Feasible Mates

我们可以索引图节点的属性，以快速检索可行的配偶。这避免了对大图中所有节点的顺序扫描。甚至减少了Φ（ui）的大小此外，我们还可以超越节点，考虑节点的邻域子图。邻里信息可以在早期阶段被用来修剪不可行的配偶。
定义7。（邻域子图）给定图G、节点v和半径r，节点v的邻域子图由距离r（跳数）内的所有节点以及节点之间的所有边组成。
只有当ui的邻域子图与v的邻域子图子同构（将ui映射到v）时，节点v才是节点ui的可行配偶。注意，如果半径为0，那么邻域子图将退化为节点。
虽然邻域子图具有较高的剪枝能力，但它们需要产生较大的计算开销。这种开销可以通过用它们的轻量级轮廓来表示邻域子图来减少。例如，可以将前文件按字典顺序定义为节点标签的序列。然后，剪枝条件就变成了一个配置文件是否是另一个配置文件的子序列。

为了方便起见，图12再次显示了样本图模式P和数据库图G。图13显示了半径为1的邻域子图及其对g节点的轮廓。如果使用节点属性检索可行的配偶，则搜索空间为{A1，A2}×{B1，B2}×{C1，C2}。如果使用邻域子图检索可行的配偶，则搜索空间为{A1}×{B1}×{C2}。最后，如果使用配置文件检索可行的配偶，那么搜索空间为{A1}×{B1，B2}×{C2}。这些内容如图13的右侧所示。

如果节点属性是有选择性的，例如，有许多唯一的属性值，那么就可以使用b树或散列表来索引节点属性，并存储邻域子图或配置文件。检索是通过对节点属性的索引访问来完成的，然后使用邻域子图或配置文件进行修剪。否则，如果节点属性不是选择性的，则可能必须对邻域子图或轮廓进行索引。最近的图形索引技术[7,15,19,29,31,34,35,36,37]或多维索引方法，如r-树，可以用于此目的。

4.3 Joint Reduction of Search Space

我们通过伪子图同构的重新细化过程迭代地减少整个搜索空间，这是之前在[15]中开发的一种近似算法。从本质上说，这种技术检查每个节点u及其可行的伴侣v是否相邻子树uP是亚同构的v在g这个检查可以递归的深度相邻子树：u的l子树是亚同构的v只有一个二部图Bu，v邻居u和v之间有一个半完美的匹配，也就是说，所有的邻居u是匹配的。在l级的二部图中，只有当u的l级−1子树与v的子树次同构时，两个节点u和v之间才存在一条边。
算法2概述了细化过程。在每次迭代中（第3-18行）中，为每个u及其可行的matev（第5-9行）构造一个二部图Bu，v。如果Bu，v没有半完美匹配，则从Φ(u)中删除v，从而减少了搜索空间（第13行）。

该算法在[15]中讨论的细化过程上有两个实现改进。首先，它避免了不必要的二部图匹配。如果需要检查一对% u，v&，则需要进行半完美匹配(第2行，4).如果存在半完美匹配，那么这对匹配就没有被标记（第10-11行）。否则，从Φ(u)（第13行）中去除v可能会影响邻近的%u”、v”&对的半完美匹配的存在。结果，这些对被再次标记和检查（第14行）。其次，%u、v和对将使用哈希表而不是矩阵来存储和操作。这将空间和时间复杂度从O（k·n）降低到O（“k i=1 |Φ（ui）|）。整体时间复杂度是O (l·“k i=1 |Φ（ui）|·（d1d2+M（d1d2））l细化水平，d1和d2分别最大程度的P和G，和M（）最大二部匹配（O（n2.5）霍普克罗夫特和卡普的算法[16]）。
图14显示了图12中示例中算法2的执行。在第1级，A2和C1分别从Φ(A)和Φ©中移除。在第2级，B2从Φ(B)中移除，因为二部图BB，B2没有半完美匹配（注意A2已经从Φ(A)中移除）。

而在第4.2节中讨论的邻域子图利用局部信息来修剪不可行的对象，而算法2中的细化过程则从全局的角度来修剪搜索空间。全局剪枝具有较大的开销，并且依赖于局部剪枝的输出。因此，这两种修剪方法都是不可或缺的，应该一起使用。

4.4 Optimization of Search Order

接下来，我们考虑算法1的搜索顺序。这里的目标是为节点找到一个好的搜索顺序。由于搜索过程等价于多个连接，因此它类似于一个典型的查询优化问题[5]。需要考虑两个主要问题。一个是给定搜索顺序的成本模型。另一种是寻找良好的搜索顺序的算法。利用成本模型作为搜索算法的目标函数。由于搜索算法是相对标准的（如，动态规划，贪婪算法），我们关注成本模型，并说明它可以在图的领域中被定制。

4.4.1 Cost Model

一个搜索顺序（又名查询计划）可以表示为一个有根的二叉树，其叶子是图模式的节点，每个内部节点都是一个连接操作。图15显示了搜索订单的两个示例。

我们将一个连接（查询计划树中的一个节点）的成本估计为要连接的集合的基数的乘积。叶节点的基数是可行配偶的数量。内部节点的基数可以估计为由因子γ减少的集合基数的乘积。
定义8。（连接的结果大小）连接i的结果大小估计为

其中，i.left和i.right分别为i的左右子节点，γ(i)为还原因子。
估计还原因子γ(i)的一种简单方法是用一个常数来近似它。一种更详细的方法是考虑连接中的边的概率：设E (i)是连接i中涉及的边的集，然后

其中，P（e（u，v））是基于u和v条件的边e (u，v）的概率。这个概率可以估计为

其中，freq（）表示大图中的边或节点的频率。
定义9。（一个连接的成本）连接的成本i被估计为

定义10。（搜索订单的成本）搜索订单Γ的总成本被估计为

例如，让输入的搜索空间为{A1}×{B1，B2}×{C2}。如果我们使用一个恒定的减少因子γ，那么成本（a&B）=1×2=2，Size（a&B）=2γ，成本（a&B）&C)=2γ×1=2γ。总成本为2 + 2γ。同样，（A&C）&B的总成本是1 + 2γ。因此，搜索顺序（A&C）&B优于（A&B）&C。

4.4.2 Search Order

所有可能的搜索顺序的数量以节点的数量呈指数增长。列举所有这些东西都是很昂贵的。正如在许多查询优化技术中一样，我们只考虑左-深的查询计划，即每个连接的外部节点总是一个叶节点。传统的动态规划将需要一个O（2k）的时间复杂度大小为k的图形模式。这是不能扩展到大型图形模式。因此，我们在实现中采用了一种简单的贪婪方法：在连接i时，选择一个使连接的估计成本最小化的叶节点。

5. EXPERIMENTAL STUDY

在本节中，我们将评估所提出的访问方法在大型真实图和合成图上的性能。访问方法是用JunJDK1.6用Java编写的。
为了进行比较，我们实现了如图2所示的基于sql的图模式匹配方法，如图所示，只是只返回一个结果计数，以最小化通信成本。我们使用MySQL 5.0.45作为数据库服务器。MySQL配置为：存储引擎=MyISAM（非事务性），密钥缓冲区大小为=256M。其他参数则设置为默认值。对于每个大图，都创建了两个表V（vid，标签）和E（vid1，vid2），如图2所示。为表中的每个字段构建b树索引。所有的实验都是在AMDAthlon64X2 4200+2.2 GHz机器上运行的，2GB内存，运行MS Win XP Pro。

5.1 Biological Network

我们实验了一个酵母蛋白相互作用网络[1]。该图由3112个节点和12519条边组成。每个节点代表一个独特的蛋白质，每条边代表蛋白质之间的相互作用。
为了允许进行有意义的查询，我们将基因本体论（GO）的[12]信息添加到蛋白质中。这个本体论是描述基因及其产物（蛋白质）的细胞成分、生物过程和分子功能的类别层次。每个GO术语都是层次结构中的一个节点，并且有一个或多个父GO术语。每种蛋白质都有一个或多个GO术语。酵母网络中最初的GO术语由2205个不同的标签组成。我们通过使用它们的高级祖先来放松这些GO术语，它们由183个不同的标签组成。这种放松使我们能够找到更有意义和一般的模式。与此同时，这使问题更困难，因为标签的选择性更低。我们使用散列表对节点标签进行索引，并存储半径为1的邻域子图和轮廓。
我们使用两种极端类型的图作为查询来评估访问方法：团系和路径。对于生物数据集，前者可能对应于蛋白质复合物，而后者可能对应于转录或信号通路。

5.1.1 Clique Queries

我们通过将团的大小从2改变到7（大小大于7没有答案）来生成团查询。对于每个大小，我们生成一个完整的图，并为每个节点分配一个随机的标签。随机标签是从前40个最常见的标签中选择的。我们生成1000个小团查询，并将结果取平均值。根据返回的答案数量，查询被分为两组：低点击率（少于100个答案）和高点击率（超过100个答案）。没有答案的查询不被计算在统计数据中。如果一个查询有太多的命中次数（超过1000次），那么图形模式匹配将立即终止，并将该查询在高命中次数组中计数。
我们评估了检索方法的剪枝能力通过将得到的搜索空间与基线搜索空间进行比较。基线搜索空间由仅通过检查节点属性组成的可行的配偶组成。搜索空间的缩减比被定义为

其中，Φ0为基线搜索空间。
图16显示了不同方法对搜索空间的缩减率。“通过配置文件检索”通过检查配置文件找到可行的配偶，“通过子图检索”通过检查邻域子图找到可行的配偶（第4.2节）。“细化搜索空间”是指通过第4.3节中讨论的细化步骤减少搜索空间（输入搜索空间由“通过配置文件检索”生成）。在细化步骤中，将最大细化级别+设置为查询的大小。从图中可以看出，细化过程总是减少了由专业文件检索到的搜索空间。通过子图进行检索的结果是在最小的搜索空间中。这是由于一个团查询的邻域子图实际上是整个团。

图17(a)显示了不同团大小下单个步骤的平均处理时间。各个步骤包括按轮廓检索、按子图检索、细化、使用优化顺序的搜索（第4.4节），以及没有优化顺序的搜索。寻找优化顺序的时间可以忽略不计，因为我们在实现中采用了贪婪的方法。如图所示，子图检索产生的搜索空间比轮廓检索产生的搜索空间更小，但开销很大。另一个观察结果是，优化后的顺序提高了搜索时间。
图17(b)显示了与基于sql的方法对低命中率查询相比的平均总查询处理时间。“优化”处理包括检索由配置文件，优化，搜索顺序的优化，和搜索与优化的顺序。“基线”处理包括按节点属性检索和在基线空间上没有优化顺序的搜索。在“优化”的情况下，由于搜索空间的减少，大大提高了查询处理时间。

基于sql的方法需要更长的时间，并且不能扩展到大的团查询。这是由于未修剪的搜索空间和所涉及的大量连接。我们的图模式匹配算法（第4.1节）在节点数上是指数级的，而基于sql的方法在边数上是指数级的。例如，一个大小为5的小团有10条边。这需要在节点和边之间进行20个连接（如图2所示）。

5.1.2 Path Queries

我们所考虑的第二类查询是在连通性的另一个极端：路径查询。这个查询的大小在2到10之间变化。细化步骤的输入搜索空间是“按概要文件检索”。其他的设置也类似于对小团体的查询。
图18显示了路径查询的缩减比率。与团查询不同，这里的细化步骤（第4.3节）产生了最小的搜索空间。这是因为重新细化步骤减少了整个搜索空间，而局部剪枝（通过配置文件或通过子图）不能捕获全局信息。

图19(a)显示了路径查询的单个时间（由于值较小，一些图不可见）。各个步骤比小团体查询所花费的时间要少。这是因为路径查询比团查询更简单。搜索步骤（有和没有优化的顺序）可以忽略不计。这是由细化步骤产生的小搜索空间的结果。图19(b)显示了路径查询的总时间。“优化”的专业人士这里的搜索包括通过配置文件进行检索、细化、优化搜索顺序和使用优化顺序的搜索。同样，“优化”处理在“基线”处理上大大改进。基于sql的处理比团查询的规模更好，因为路径查询需要的连接数量更少。但它仍然比“优化”处理需要更多的时间。

5.2 Synthetic Graphs

我们还评估了在合成图上的访问方法。合成图采用简单的˝-˝[11]随机图模型生成：生成n个节点，然后随机选择两个端节点生成m条边。每个节点都被分配了一个标签（总共有100个不同的标签）。标签的分布遵循Zipf定律，即第x个标签p (x)的概率与x−1成正比。这些查询是通过从合成图中随机提取一个已连接的子图来生成的。
我们首先将合成图的大小n固定为10K，m = 5n，并将查询的大小改变在4到20之间。图20和图21(a)显示了搜索空间和时间。我们发现最好的组合是轮廓检索，然后是细化步骤，以优化的顺序搜索。同样，由于细化步骤产生的搜索空间较小，搜索步骤花费的时间很少。基于SQL的处理需要更长的时间，并且不适用于大型查询。

然后，我们将查询大小设置为4，并将合成图的大小n改变在10K到320K之间，以及m = 5n。图21(b)显示了总时间。可以看出，在增加图形大小方面，“优化”处理比“基线”处理的规模更好。基于sql的方法也可以扩展到小查询的大型图，但它仍然比“优化”处理需要更长的时间。
总结我们的实验，配置文件检索产生的搜索空间很小，开销很小。细化步骤（第4.3节）大大减少了搜索空间。搜索空间的广泛减少可以很好地补偿了搜索步骤的开销。实际的组合是通过配置文件进行检索，然后进行细化，然后以优化的顺序进行搜索。这种组合可以很好地扩展不同的查询大小和图形大小。基于SQL的处理不能可扩展到大型查询。总的来说，优化后的处理性能比基于sql的方法好一个数量级。虽然基于sql的实现可以通过仔细的调优和其他优化来实现微小的改进，但结果表明，在图域中的查询处理具有明显的优势。

6. RELATED WORK

人们已经为图形提出了许多查询语言。图形日志[10]将数据和查询都表示为图形。在表达能力方面，GraphLog与分层线性数据日志相当。GOOD [14]是一个面向图的对象数据模型，它通过节点和边的添加和删除来转换图。GraphDB [13]使用一个面向对象的数据库图形和查询数据模型。GOQL [30]还使用了一个面向对象的图形数据模型，并且是对OQL的一个扩展。PQL [21]是一种用于生物网络的路径查询语言。该语言来源于SQL，并在RDBMS之上实现。
语义Web和附带的SPARQL查询语言[23]激发了最近对图查询语言的一些兴趣。该模型通过一组三元组来描述一个图，每个三元组描述一个（属性、值）对或两个节点之间的互连。SPARQL查询语言主要通过对单个节点进行约束的模式来工作。该模式的所有可能的匹配都将从图形数据库中返回。通过提供用于同时表达对整个结果图的约束的原语，通用的图查询语言可以更加强大。
在XML数据库中，TAX [18]是一个针对XML的树形代数。TAX使用一个模式树来匹配有趣的节点。模式树由树的结构和树的节点上的谓词组成。GraphQL将这个想法推广到描述一个图形模式。
GraphQL与上面的查询语言不同，它选择图作为基本单元。与SQL相比，GraphQL也有一个类似的代数系统，但代数算子是直接在图上定义的。与OODB相比，GraphQL查询是面向设置的，而OODB则以导航的方式访问对象。在数据表示方面，GraphQL是半结构化的，不在图上转换严格的和预定义的数据类型或模式。相反，SQL假定有一个严格的模式来存储数据。此外，GraphQL可以使用图的优化有效地实现。表1概述了GraphQL和其他查询语言之间的主要区别。

图形语法以前已经被用于在各个领域的[26,25]中建模可视化语言和图形转换。我们的工作的不同之处在于，我们的重点是查询语言和数据库实现。
在图索引中，GraphGrep [29]使用枚举路径作为索引特征来过滤不匹配的图。GIndex [35]使用有区别的频繁片段作为索引特征提高过滤率和减少索引大小。闭形树[15]使用图闭包作为边界框将图组织成基于树的索引结构。GString [19]将图查询转换为子序列匹配。TreePi [36]使用频繁的子树作为索引特征。威廉姆斯等人。[34]分解图，并散列所得到的子图的规范形式。SAGA [31]枚举图的片段，通过组装查询片段生成答案。FG-index [7]使用频繁的子图作为索引特征。频繁的图形查询不需要验证而得到回答，而不频繁的查询只需要少量的验证。Zhao等[37]表明，频繁树特征加少量判别图优于频繁图特征。虽然上述技术可以用作大量小图的访问方法，但本文讨论了单个大图的访问方法。
另一行图索引地址是大型有向图[6,8,9,27,32,33]中的可达性查询。在可达性查询中，给出两个节点，答案是这两个节点之间是否存在一条路径。可达性查询对应于递归路径模式，这是路径（图3(e))。可达性查询的索引和处理通常基于生成树，使用前/后顺序标记[6,32,33]或2跳覆盖[8,9,27]。这些技术可以合并到递归图模式查询的访问方法中。

7. CONCLUSION

我们提出了GraphQL，一种用于具有任意属性和大小的图形的新查询语言。GraphQL有许多吸引人的特性。图是基本的单位，而图的结构是使用图的形式语言的概念进行可组合的。我们利用邻域子图和轮廓的思想，优化整体搜索空间和优化搜索顺序，开发了有效的选择算子访问方法。在真实图和合成图上的实验研究验证了访问方法。
总之，图在多个领域中普遍存在。本文演示了使用本地图进行查询和数据库实现的好处。将图转换为关系是不自然的，不能利用特定于图的启发式。从表达性和实现技术的角度来看，基于图的查询和基于图的本地数据库的耦合产生了有趣的可能性。我们几乎没有触及表面，在将查询和数据库的特征与适当的启发式相匹配方面还需要做更多的工作。本文的研究结果是这方面重要的第一步。