一种艺术般的问题解决办法-----递归

The words written in front

大家好，我是xiaoxie,希望你看完之后对你能有所帮助，不足之处，请批评指正！

希望可以和大家一起交流学习进步！

一.引言

1.递归

递归算法（英语：recursion algorithm）在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。递归式方法可以被用于解决很多的计算机科学问题，因此它是计算机科学中十分重要的一个概念。绝大多数编程语言支持函数的自调用，在这些语言中函数可以通过调用自身来进行递归。计算理论可以证明递归的作用可以完全取代循环，因此在很多函数编程语言（如c++）习惯用递归来实现循环，它可以让人分成三个阵营看待它；讨厌它的，喜欢它的，以及以前讨厌在经过一段时间后彻底喜欢上它的，我相信在你阅读我这篇文章，你应该会对这一种优雅，艺术般的问题解决办法产生一点内心中不一样的看法。

二.方法介绍

1.例子说明

假如你要找一把钥匙，而钥匙在一个箱子里的某个地方，而你想起来，钥匙好像在某个盒子里，而盒子里面还有盒子，而钥匙就在其中某个盒子里，该若何用代码去解决这个问题呢，首先我想大部分人会这样想

2.过程

1.创建一个要找的箱子堆。

2.从箱子堆里随机找一个箱子，打开它

3.如果打开的是钥匙，成功找到。

4.如果打开的是箱子就放回去。

5.再继续第二步，直到箱子堆里箱子为空

3.伪代码实现

常量 MAX_BOXES = 10  // 箱子堆的最大大小

变量 box_stack[MAX_BOXES]  // 字符指针数组，存储箱子堆中的箱子
变量 num_boxes = 0  // 箱子堆中箱子的数量

// 创建箱子堆
过程 创建箱子堆
输入：箱子堆的大小 num_boxes
输出：无

对于 i 从 1 到 num_boxes 循环：
    创建一个名为 box_name 的字符串，内容为 "箱子" + i
    分配一个大小为 10 的字符数组 box
    将 box_name 复制到 box 中
    将 box 存储到 box_stack[i-1] 中
结束过程

// 打乱箱子堆的顺序
过程 打乱箱子堆的顺序
输入：无
输出：无

使用当前时间作为随机数种子
对于 i 从 num_boxes-1 到 1 循环：
    随机生成一个范围在 0 到 i 的整数 j
    交换 box_stack[i] 和 box_stack[j]
结束过程

// 寻找钥匙的过程
过程 寻找钥匙
输入：无
输出：无

读取箱子堆的大小 num_boxes
创建箱子堆，大小为 num_boxes
打乱箱子堆的顺序

对于 i 从 num_boxes-1 到 0 循环：
    获取箱子堆中的第 i 个箱子 box
    打开箱子 box
    如果 box 是钥匙：
        输出 "成功找到钥匙！"
        退出循环
    否则：
        输出 "里面是一个箱子，继续寻找。"
    释放 box
结束过程

如果循环结束后仍未找到钥匙：
    输出 "箱子堆里的箱子已经全部打开，但没有找到钥匙。"

    
   

4.递归过程

1.检查箱子里的每一个东西。

2.如果里面是箱子，就回到第一步。

3.如果里面是钥匙，就成功找到了。

5.伪代码实现

function findKey(box):
    for item in box:
        if item is a key:
            return item
        else if item is a box:
            return findKey(item)
    return null

# 主程序
startingBox = getStartingBox()  # 获取起始盒子
key = findKey(startingBox)  # 调用递归函数查找钥匙
if key is not null:
    print("找到钥匙！")
else:
    print("未找到钥匙。")

6.说明

其实在这种情况下无论使用递归还是循环，二者在性能方面并没有优劣之分，只是递归可以让解决方案变得更加清晰，递归可以把一件事情拆分成许多小事情，这就是所谓的大事化小。，而且在一些情况之中，使用循环比递归的性能更好。你可能听到这句话觉得那还学什么递归，博主想说的是递归可以更好的理解问题，并且在后期学习的时候，用很多算法都应用了递归这一思想，所以呢学好递归还是很重要的，无论你喜不喜欢用它。

三.递归的应用----解决汉诺塔问题

1.汉诺塔问题

汉诺塔问题源自印度一个古老的传说，印度教的“创造之神”梵天创造世界时做了 3 根金刚石柱，其中的一根柱子上按照从小到大的顺序摞着 64 个黄金圆盘。梵天命令一个叫婆罗门的门徒将所有的圆盘移动到另一个柱子上，移动过程中必须遵守以下规则：
每次只能移动柱子最顶端的一个圆盘；
每个柱子上，小圆盘永远要位于大圆盘之上。

 三圆盘汉诺塔

1.过程

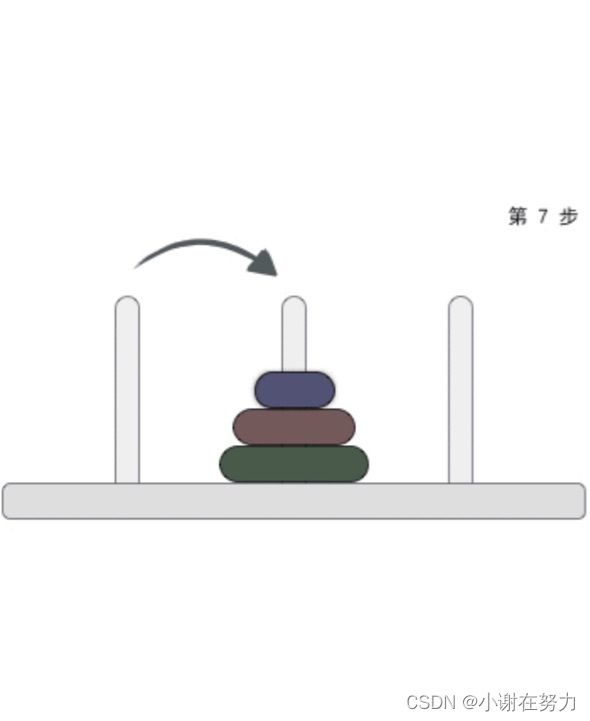
当柱子上有三个圆盘时（如下图），为了表示方便，以A、B、C依次代表从左至右三根柱子。其移动步骤如下：
step1：小：A->B，中：A->C，小：B->C，
step2：大：A->B，
step3：小：C->A，中：C->B，小：A->B
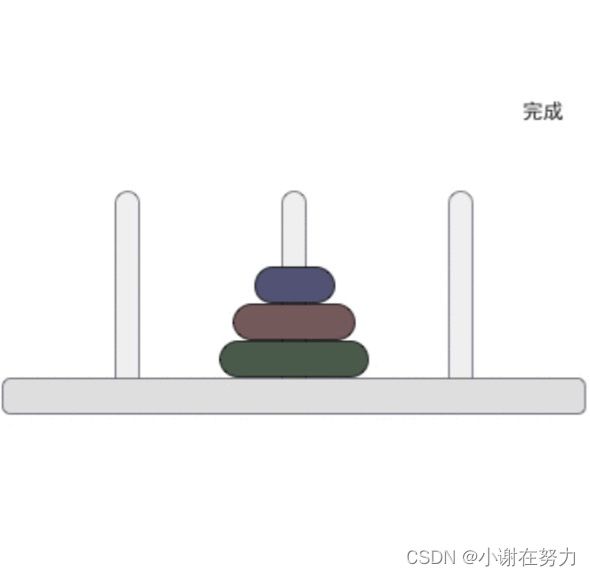
这样7步后我们便完成了移动

2.图解

3.递归解决汉诺塔问题思路

1.假设有三个柱子，分别为A、B、C，初始时所有的盘子都在A柱子上，目标是将所有的盘子从A柱子移动到C柱子上。

2.对于n个盘子的情况，可以将问题分解成三个步骤：a.将n-1个盘子从A柱子移动到B柱子上；b.将第n个盘子从A柱子移动到C柱子上；c.将n-1个盘子从B柱子移动到C柱子上。

3.对于步骤a和步骤c，可以再次调用相同的递归函数来解决子问题。递归的终止条件是当只有一个盘子时，直接将其从A柱子移动到C柱子上。

4.代码实现

根据上述思路，可以编写一个递归函数来解决汉诺塔问题。

#include 

void hanoi(int n, char source, char target, char auxiliary) {
    if (n > 0) {
        // 将n-1个盘子从source柱子移动到auxiliary柱子上
        hanoi(n-1, source, auxiliary, target);

        // 将第n个盘子从source柱子移动到target柱子上
        printf("Move disk %d from %c to %c\n", n, source, target);

        // 将n-1个盘子从auxiliary柱子移动到target柱子上
        hanoi(n-1, auxiliary, target, source);
    }
}

int main() {
    int n = 3;
    char source = 'A';
    char target = 'C';
    char auxiliary = 'B';

    hanoi(n, source, target, auxiliary);

    return 0;
}

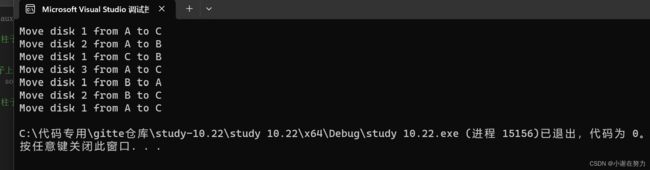
输出结果为：

5.循环的思想

当然使用循环也可以汉诺塔的问题，大概思路如下：

1. 根据盘子数量确定总共需要移动的次数，公式为 total_moves = (1 << n) - 1，其中 n 是盘子的数量。

2. 如果盘子数量是奇数，则交换目标柱子和辅助柱子的位置。

3. 使用循环从1到总移动次数，依次执行以下步骤：

   • 如果当前移动次数是1的倍数，则将最小的盘子从源柱子移动到目标柱子。
   • 如果当前移动次数是2的倍数，则将最小的盘子从源柱子移动到辅助柱子。
   • 如果当前移动次数是3的倍数，则将最小的盘子从辅助柱子移动到目标柱子。

4. 重复步骤3，直到完成所有的移动。

下面是使用循环实现汉诺塔问题的示例代码：

#include 

void hanoi(int n, char source, char target, char auxiliary) {
    int i, total_moves;
    char temp;
    
    // 根据盘子的数量确定总共需要移动的次数
    total_moves = (1 << n) - 1;
    
    // 如果盘子数量是奇数，则交换目标柱子和辅助柱子的位置
    if (n % 2 == 1) {
        temp = target;
        target = auxiliary;
        auxiliary = temp;
    }
    
    for (i = 1; i <= total_moves; i++) {
        if (i % 3 == 1) {
            printf("Move disk %d from %c to %c\n", i, source, target);
        } else if (i % 3 == 2) {
            printf("Move disk %d from %c to %c\n", i, source, auxiliary);
        } else if (i % 3 == 0) {
            printf("Move disk %d from %c to %c\n", i, auxiliary, target);
        }
    }
}

int main() {
    int n = 3;
    char source = 'A';
    char target = 'C';
    char auxiliary = 'B';

    hanoi(n, source, target, auxiliary);

    return 0;
}

四.对递归的看法

从上述示例中，我们可以看到循环和递归都可以解决这一系列问题，不过我们可以明显的看出使用递归后，我们可以把一个复杂的问题简化成一个个简单的小问题，这就是所谓的大事化小，这也是为什么递归让我着迷的地方，它可以把一个复杂的繁琐的问题如艺术般的转换成简单的，容易理解的问题，当然它也有缺点比如 ：1.内存消耗；2.时间复杂度高；3.  可能导致栈溢出；4.可能陷入无限循环等等；但它也有简洁明了，可读性高等等优点，无论是选择循环还是递归，亦或者是其他什么的算法，适合才是最重要的！希望你阅读完后可以使你对递归有不同的看法，谢谢大家的阅读，不足之处，请多多谅解，让我们一起共同学习共同成长。