训练数据集和测试数据集的意义

目录

一、模型泛化能力

二、学习曲线

三、总结

---

一、模型泛化能力

---

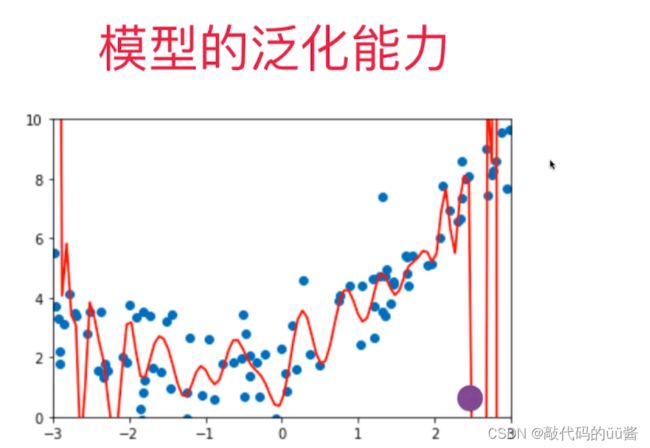
当我们训练一个模型时，目的不是最大程度的拟合这些点，而是为了获得一个可预测的模型，即当有了新的样本，新的数据可以在该模型中得到很好的解答。基于此，但我们去衡量模型时，评判训练数据在模型的拟合程度有多好是没有意义的，我们真正需要的是能够衡量该模型算法能力有多好。

在这种情况下，我们使用训练测试数据集的分离，即将原数据集分成训练数据集和测试数据集。测试数据集对于模型来说就是全新数据集，如果测试数据集最终拟合程度很好就说明这个模型的泛化能力是很强的。

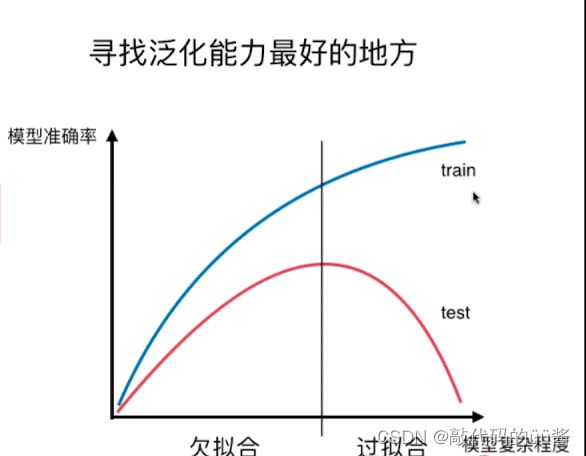
欠拟合就是算法所训练的模型不能完整表述数据关系。而过拟合就是指算法所训练的模型过多地表达了数据间的噪音关系。

二、学习曲线

---

学习曲线也可以看出模型是欠拟合还是过拟合。学习曲线就是随着训练样本的逐渐增多，算法训练出的模型的表现能力。

代码示例：

import numpy as np
import matplotlib.pyplot as plt

#生产随机数据
np.random.seed(666)
x = np.random.uniform(-3.0,3.0,size=100)
X = x.reshape(-1,1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0,1,size=100)

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 10)
#X_train.shape

train_score = []
test_score = []
for i in range(1,76):
    lin_reg = LinearRegression()
    lin_reg.fit(X_train[:i],y_train[:i])
    
    y_train_predict = lin_reg.predict(X_train[:i])
    train_score.append(mean_squared_error(y_train[:i],y_train_predict))
    
    y_test_predict = lin_reg.predict(X_test)
    test_score.append(mean_squared_error(y_test,y_test_predict))

#生产学习曲线
plt.plot([i for i in range(1,76)],np.sqrt(train_score),label="train") #rmse
plt.plot([i for i in range(1,76)],np.sqrt(test_score),label="test") 
plt.legend()
plt.show()

运行结果：

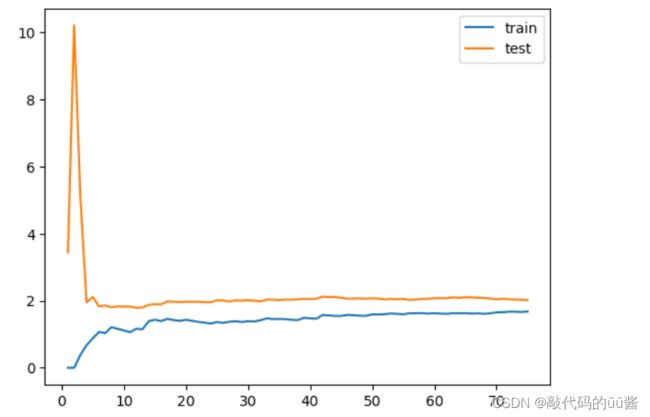
对线性回归模型来说得到的学习曲线如图所示。该曲线大体趋势上很明显训练数据集上相应的误差是逐渐升高的，由于我们的训练数据越来越多，那么对应数据点难以合并所有数据，所以相应的误差会逐渐的累积。但这个误差的累积到了一定程度后，它的累积变化是非常小的。

对于测试数据集进行训练时，刚开始测试误差非常的大，但当我们的训练量到一定程度时，测试的误差会逐渐减小到一定程度，达到一种相对稳定的状态。训练误差和测试误差区域大体是在一个级别上，不过测试误差会比训练误差高，是因为我们训练数据拟合过程可以把训练数据集拟合得比较好，相对的误差小一些，但是泛化到测试数据上时还是有可能多一些误差。

代码示例：

#生产学习曲线
def plot_learning_curve(algo,X_train,X_test,y_train,y_test):
    
    train_score = []
    test_score = []
    
    for i in range(1,len(X_train)+1):
        algo.fit(X_train[:i],y_train[:i])

        y_train_predict = algo.predict(X_train[:i])
        train_score.append(mean_squared_error(y_train[:i],y_train_predict))

        y_test_predict = algo.predict(X_test)
        test_score.append(mean_squared_error(y_test,y_test_predict))
    
    plt.plot([i for i in range(1,len(X_train)+1)],np.sqrt(train_score),label="train") #rmse
    plt.plot([i for i in range(1,len(X_train)+1)],np.sqrt(test_score),label="test") 
    plt.legend()
    plt.axis([0,len(X_train)+1,0,4])
    plt.show()
    
plot_learning_curve(LinearRegression(),X_train,X_test,y_train,y_test)


from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler

#管道
def PloynomialRegression(degree):
    return  Pipeline([
    ("ploy",PolynomialFeatures(degree = degree)),
    ("std_scaler",StandardScaler()),
    ("lin_reg",LinearRegression())
])

poly2_reg = PloynomialRegression(degree=2)
plot_learning_curve(poly2_reg,X_train,X_test,y_train,y_test)

运行结果：

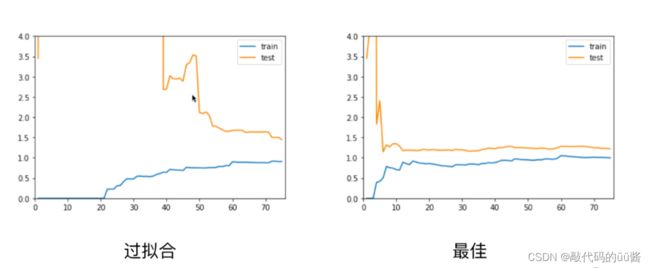
对比线性回归的学习曲线，它的误差稳定在大概是 1.7这个位置，而对于我们的二阶的多项式回归，这个学习曲线误差稳定在 1 左右，即它稳定的位置相对的比较低，这说明了使用二阶的多项式回归进行数据训练结果是比较好的。

三、总结

---

通过对比我们可以看出，欠拟合无论对于训练数据集来说还是对于测试数据集来说，相应的误差都比较大，这是因为我们本身模型选的就不对，所以即使在训练数据上，它的误差也是大的，就会呈现这样的一种姿态。

对于过拟合的情况，在训练上相应的它的误差不大，但是问题在于测试数据集的误差相对是比较大的，并且测试数据集的这个误差离训练数据集的这个误差比较远，他们之间的差距比较大，这就说明了此时我们的这个模型相应的泛化能力不够好，对于新的数据来说误差是比较大的。