洛谷 P4513 小白逛公园

经典系列

分析

• 很清晰，此题的难点在于如何维护最大子段和，也是经典所在。
• 最大子段和有三种情况，分别为中线左边，中线右边，跨越中线，如下：
  
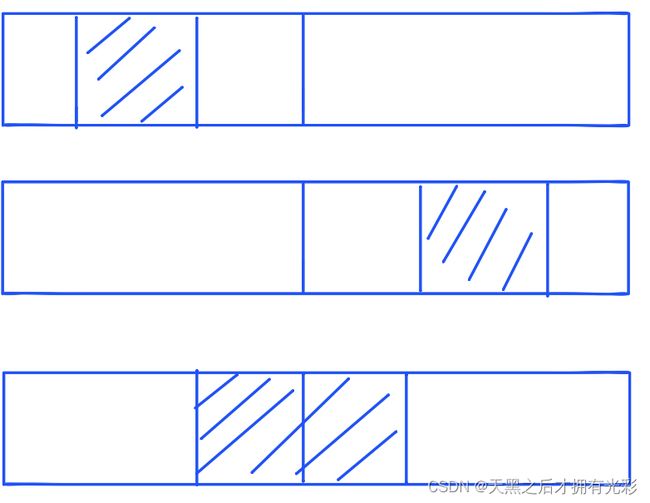
• 此时我们需要维护三个变量最大前缀子段和，最大后缀子段和，最大子段和。为什么？你会发现对于不跨越中线的最大子段和，我们可以直接由儿子节点向父亲节点传递$tr[i].maxx=max(tr[i\ast 2].maxx,tr[i\ast 2+1].maxx)$ $maxx$表示最大子段和 。而跨越中线刚好是左儿子最大后缀和加上右儿子最大前缀和。所以整合为：$tr[i].maxx=max(tr[\ast 2].maxr+tr[i\ast 2+1].maxl,max(tr[i\ast 2].maxx,tr[i\ast 2+1].maxx))$ $maxl,maxr$分别表示最大前缀后缀子段和
• 对于最大前缀子段和的更新又有两种情况分别为中线左边，跨越中线，如下后缀和同理 ：
  
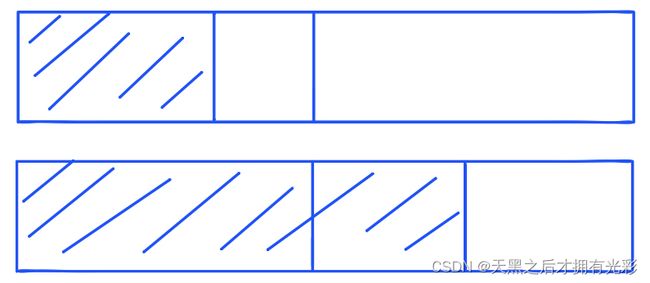
  同样不难得到对于中线左边的可以直接由儿子节点向父亲节点传递 $tr[i].maxl=tr[i\ast 2].maxl$ 。跨越中线左区间全部包含为 $tr[i].maxl=tr[i\ast 2].sum+tr[i\ast 2+1].maxl$ ，整合为 $tr[i].maxl=max(tr[i\ast 2].maxl,tr[i\ast 2].sum+tr[i\ast 2+1].maxl)$
  $modify$ 代码如下：

void pushup(int i)
{
    tr[i].sum=tr[ls].sum+tr[rs].sum;
    tr[i].maxl=max(tr[ls].maxl,tr[ls].sum+tr[rs].maxl);
    tr[i].maxr=max(tr[rs].maxr,tr[rs].sum+tr[ls].maxr);
    tr[i].maxx=max(tr[ls].maxr+tr[rs].maxl,(max(tr[ls].maxx,tr[rs].maxx)));
}

• 此题还有另一个难点就是在查询的途中当需要二分区间时，你可能会很简单的想到分别找最大子段和选最大的不就好了，很遗憾错了。你避开了跨越中线这种情况，所以在此处你需要在二分区间后整合一下所以查询返回的是结构体，如下：

p query(int i,int l,int r)
{
    if(l<=tr[i].l&&tr[i].r<=r) return tr[i];
    if(tr[ls].r>=l&&tr[rs].l<=r)
    {
        p t,tpl=query(ls,l,r),tpr=query(rs,l,r);
        t.sum=tpl.sum+tpr.sum;
        t.maxl=max(tpl.maxl,tpl.sum+tpr.maxl);
        t.maxr=max(tpr.maxr,tpr.sum+tpl.maxr);
        t.maxx=max(tpl.maxr+tpr.maxl,(max(tpl.maxx,tpr.maxx)));
        return t;
    }
    else if(l<=tr[ls].r) return query(ls,l,r);
    else return query(rs,l,r);
}

• 除去个人习惯，总共维护四个变量分别为 $maxx$ 最大子段和 $maxl$ 最大前缀子段和 $maxr$ 最大后缀子段和 $sum$ 子段和

Think Twice, Code Once

#include
#define il inline
#define get getchar
#define put putchar
#define is isdigit
#define re register
#define int long long
#define min(a,b) a<b?a:b
#define max(a,b) a>b?a:b
#define dfor(i,a,b) for(re int i=a;i<=b;++i)
#define dforr(i,a,b) for(re int i=a;i>=b;--i)
#define dforn(i,a,b) for(re int i=a;i<=b;++i,put(10))
#define mem(a,b) memset(a,b,sizeof(a))
#define memc(a,b) memcpy(a,b,sizeof a)
#define pr 114514191981
#define gg(a) cout<<a,put(32)
#define INF 0x7fffffff
#define tt(x) cout<<x<<'\n'
#define ls i<<1
#define rs i<<1|1
#define la(r) tr[r].ch[0]
#define ra(r) tr[r].ch[1]
#define lowbit(x) (x&-x)
using namespace std;
typedef unsigned int ull;
typedef long long ll;
int read(void)
{
    re int x=0,f=1;re char c=get();
    while(!is(c)) (f=c==45?-1:1),c=get();
    while(is(c)) x=(x<<1)+(x<<3)+(c^48),c=get();
    return x*f;
}
void write(int x)
{
    if(x<0) x=-x,put(45);
    if(x>9) write(x/10);
    put((x%10)^48);
}
#define writeln(a) write(a),put(10)
#define writesp(a) write(a),put(32)
const int N=5e5+10,M=5e5+10,SN=1e3+10,mod=998244353;
int n,m,a[N];
struct p
{
    int l,r,sum,maxx,maxl,maxr;
    p(){}
    p(int l1,int r1){l=l1,r=r1;}
}tr[N<<2];
void pushup(int i)
{
    tr[i].sum=tr[ls].sum+tr[rs].sum;
    tr[i].maxl=max(tr[ls].maxl,tr[ls].sum+tr[rs].maxl);
    tr[i].maxr=max(tr[rs].maxr,tr[rs].sum+tr[ls].maxr);
    tr[i].maxx=max(tr[ls].maxr+tr[rs].maxl,(max(tr[ls].maxx,tr[rs].maxx)));
}
void build(int i,int l,int r)
{
    tr[i]=p(l,r);
    if(l==r){tr[i].maxx=tr[i].maxl=tr[i].maxr=tr[i].sum=a[l];return ;}
    int mid=(l+r)>>1;
    build(ls,l,mid),build(rs,mid+1,r);
    pushup(i);
}
void modify(int i,int l,int r,int ind,int k)
{
    if(l==r)
    {
        tr[i].sum=tr[i].maxx=tr[i].maxl=tr[i].maxr=k;
        return ;
    }
    if(tr[ls].r>=ind) modify(ls,l,tr[ls].r,ind,k);
    else modify(rs,tr[rs].l,r,ind,k);
    pushup(i);
}
p query(int i,int l,int r)
{
    if(l<=tr[i].l&&tr[i].r<=r) return tr[i];
    if(tr[ls].r>=l&&tr[rs].l<=r)
    {
        p t,tpl=query(ls,l,r),tpr=query(rs,l,r);
        t.sum=tpl.sum+tpr.sum;
        t.maxl=max(tpl.maxl,tpl.sum+tpr.maxl);
        t.maxr=max(tpr.maxr,tpr.sum+tpl.maxr);
        t.maxx=max(tpl.maxr+tpr.maxl,(max(tpl.maxx,tpr.maxx)));
        return t;
    }
    else if(l<=tr[ls].r) return query(ls,l,r);
    else return query(rs,l,r);
}
signed main()
{
    n=read(),m=read();
    dfor(i,1,n) a[i]=read();
    build(1,1,n);
    re int op,l,r;
    while(m--)
    {
        op=read(),l=read(),r=read();
        if(op&1) (l<=r?write(query(1,l,r).maxx):write(query(1,r,l).maxx)),put(10);
        else modify(1,1,n,l,r);
    }
    return 0;
}