论文笔记：DualDory- Logarithmic-Verifier Linkable Ring Signatures Through Preprocessing

Bootle, J., Elkhiyaoui, K., Hesse, J., Manevich, Y. (2022). DualDory: Logarithmic-Verifier Linkable Ring Signatures Through Preprocessing. ESORICS 2022.
https://link.springer.com/chapter/10.1007/978-3-031-17146-8_21

在这项工作中，原文作者构建了第一个具有对数签名大小和验证的可链接环签名，不需要任何可信机制。这个方案依赖于离散对数类型假设和双线性映射，通过集成改进的预处理参数，改进了DualRing的环签名，以减少环大小从线性到对数的验证时间。

dualory=Dualring+Dory
Dory is a pairing-based interactive argument，通过一次性离线预处理阶段实现对数验证时间，代替bulletproof。使DualRing的线性验证成本降至对数。

通过确定性标签进一步增强了DualDory的可链接性。更准确地说，将Pedersen承诺和知识签名结合起来，以表明标签是使用环中的一个密钥计算的。作为一个积极的副作用，我们能够预先计算签名的线性工作，当消息已知时，只需要执行恒定数量的操作。

Overview

DualRing

加入可链接性

引入了prefix linkability，其中要签名的字符串被分成两个部分:前缀$prfx$和消息$m$。如果两个签名是由同一用户创建的，则可以链接它们，并使用相同的前缀$prfx$签名消息。

构造prefix-linkable，签名者计算一个标签tag $H^{\prime }(prfx{)}^{sk}$
为了确保使用与签名其余部分相同的秘密密钥正确计算标签tag，让签名者为其秘密密钥生成Pedersen承诺$com=P^{sk}{Q}^r$，并使用基于标准sigma协议的“tag proof”来显示$com$和$tag$都使用相同的秘密密钥。（注意，不能对用户的公钥执行这种一致性检查，因为这会泄露用户的身份。）

进一步的问题。签名者可以使用DualRing来证明自己掌握环中一个私钥，但此证明与tag或com无关。解决：签名者知道$com=P^{sk}{Q}^r$对应的$sk,r$，那么他知道如何打开环$(com/p{k}_1,...,com/p{k}_n)$中某一个承诺到0，即，他们知道$r$满足$com/p{k}_i=Q^r$.
将DualRing应用于$(com/p{k}_1,...,com/p{k}_n)$，并添加tag proof产生一个LRS，其中验证者检查tag proof和以下方程:

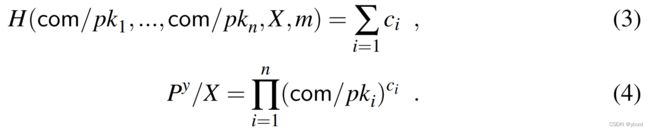
此签名的大小可在dualring中可减少到$O(logn)$。但是，验证时间仍然是$O(n)$。

同时减少签名大小和验证时间

https://link.springer.com/chapter/10.1007/978-3-030-90453-1_1
Dory方案是将bulletproof推广到双线性对：

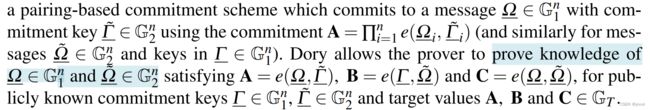
优化验证成本：Dory允许在离线阶段一劳永逸地对commitment keys 进行预处理。此后，验证者只需要对这些密钥使用简洁的承诺，并产生$O(logn)$成本。

Dory构造：

• 映射到双线性对：将（3）和（4）（prefix-Dualring验证方程）映射到双线性群上的方程。假设DualRing方案已经在双线性group的${\mathbb{G}}_1$上执行。考虑group元素$e(P,\tilde{P})$(其中$P\in {\mathbb{G}}_1,\tilde{P}\in {\mathbb{G}}_2$)。利用方程(3)的左右两边取幂，利用$e$的双线性，得到
  
  类似地，(6)可以与$\tilde{P}$配对并重新排列得到
  
  由于幂和双线性对的映射都是单射，所以方程（5）（6）包含了（3）（4）.
• 证明条件成立：给定对$(P,\dots ,P)\in {\mathbb{G}}_1^n,({\tilde{P}}^{c_1},\dots ,{\tilde{P}}^{c_n})\in {\mathbb{G}}_2^n$，$(com/p{k}_i{)}_{i=1}^n\in {\mathbb{G}}_1^n$的承诺，签名者可以使用Dory来证明公式(5)和公式(6)成立，每个方程的左侧作为目标值。注意，（5）中的目标值涉及n个值，因此为了避免这里的$O(n)$个验证器成本，我们将这些值替换为$(com/p{k}_1,\dots ,com/p{k}_n)$的承诺。只要承诺方案具有约束力，这仍然足以保证DualRing的安全性。
• 优化验证：使用$O(n)$次离线操作和$O(logn)$次在线操作来计算对$(com/p{k}_1,\dots ,com/p{k}_n)\in {\mathbb{G}}_1^n$的承诺。由于$com$依赖于随机性$r$，它对于每个签名都是不同的，因此验证者不可能独立于任何签名一劳永逸地计算这个承诺。
  相反，验证者离线计算$\tilde{\Gamma }:={\prod }_{i=1}^n{\tilde{\Gamma }}_i$，一个$(p{k}_1,\dots ,p{k}_n)$的承诺${\mathrm{A}}_0:={\prod }_{i=1}^{n}e(p{k}_i,{\tilde{\Gamma }}_i)$，这需要$O(n)$次操作。这并不依赖于签名的任何部分，并且可以为每个环“离线”计算一次，然后在“在线”签名验证中重用。请注意，承诺密钥的长度$n$给出了可以提交的用户公钥数量的上限。在验证签名时，验证者可以计算对$(com/p{k}_1,\dots ,com/p{k}_n)$的承诺$e(com,\tilde{\Gamma })/{\mathrm{A}}_0$。

Preliminaries

Argument of Knowledge

Argument of Knowledge for Pairing Products

notations

定义关系

Signature of Knowledge

Prefix-Linkable Ring Signature Schemes

tag proof

tag proof 用于证明$com$和$tag$使用了相同的$sk$，且不泄露秘密$sk,r$

$\mathbb{X}$公开参数，$\mathbb{W}$秘密参数，关系${\mathcal{R}}_{Tag}$的SoK (with message $m$)：

DualDory

(用大写字母表示group元素，小写字母表示${\mathbb{Z}}_p$元素，带~的表示${\mathbb{G}}_2$中的元素，下划$\_$表示向量，粗体表示${\mathbb{G}}_T$)

签名过程

1. 计算$com$，并用$com$迭代公钥环$p{k}_i^{\prime }$
2. 生成$p{k}^{\prime }$的承诺（为了验证的时候不再需要$O(n)$），在Dualring中代替公钥环计算hash值
   $\mathrm{A}=e(com,\tilde{\Gamma })/{\mathrm{A}}_0=e(com,{\prod }_{i=1}^n{\tilde{\Gamma }}_i)/{\prod }_{i=1}^{n}e(p{k}_i,{\tilde{\Gamma }}_i)={\prod }_{i=1}^{n}e(p{k}_i^{\prime },{\tilde{\Gamma }}_i)=e(\underline{p{k}^{\prime }},\underline{\tilde{\Gamma }})$
3. 环$\underline{p{k}^{\prime }}$上的Dualring签名，但并没有对消息$m$签名。
4. 通过关系的AoK证明双线性化的签名验证方程(5)(6)（这是为了优化验证的复杂度）：$\mathrm{B}=e({\underline{\Gamma }}^{\underline{c}},\tilde{P}),\mathrm{C}=e(Q^y/Q^x{\prod }_{i\ne j}p{k}_i^{\prime -c_i},\tilde{P})=e(Q^{r\cdot c_j}{\prod }_{i\ne j}p{k}_i^{\prime c_i},\tilde{P})=e(p{k}_j^{\prime c_j}{\prod }_{i\ne j}p{k}_i^{\prime c_i},\tilde{P})=e(\underline{p{k}^{\prime }},\tilde{P})$符合关系的定义规范，${\pi }_1$对应验证方程（6）
   类似地，${\pi }_2$对应验证方程（5）,并通过$\mathrm{A},\mathrm{B}$连接两个关系。
5. 用于耦合可链接性的tag proof(SoK)以及签名消息$m$：生成tag，和com、prfx一起作为证明的公开参数，用私密参数$(sk,r)$生成(关系+消息)的知识签名。

验证过程需要对三个证明/知识签名进行验证

1. 首先要恢复出用于验证缺少的参数：$(\mathrm{A},\mathrm{C}),(\mathrm{E})$
2. 三次验证

链接过程因为是前缀/事件链接，所以必须是同一prfx下不同消息的两个签名，由同一签名者生成，比对tag

复杂度