探索三种生成模型:基于DDPMs、NCSNs和SDEs方法的Diffusion
探索三种生成模型:基于DDPMs、NCSNs和SDEs方法的Diffusion
- 去噪扩散概率模型(DDPMs)
-
- 正向过程
- 反向过程
- 噪声条件得分网络(NCSNs)
-
- 正向过程
-
- 初始化
- 训练 NCSNs
- 生成样本
- 反向过程
- 随机微分方程(SDEs)
-
- 原理背景
- 正向过程
- 反向过程
- 模型训练与采样
- 采样方法
- 方法可行性解释
去噪扩散模型代表了计算机视觉领域的一个新兴主题,取得了在生成建模方面的显著成果。该模型分为正向扩散阶段和反向扩散阶段。在正向扩散阶段,逐步添加高斯噪声逐渐扰动输入数据;在反向扩散阶段,模型通过学习逆转扩散过程逐步恢复原始输入数据。尽管计算负担较大,但由于生成样本的质量和多样性,扩散模型受到广泛赞赏。
在计算机视觉中,扩散模型已应用于多个任务,包括图像生成、图像超分辨率、图像修复、图像编辑、图像翻译等。此外,扩散模型学到的潜在表示在判别任务中也被发现是有用的,例如图像分割、分类和异常检测。
回顾扩散模型的文章,可将扩散模型分为三个主要子类:
- 去噪扩散概率模型(DDPMs)
- 噪声条件得分网络(NCSNs)
- 随机微分方程(SDEs)
DDPMs使用潜在变量估计概率分布,类似于变分自动编码器。 NCSNs基于训练共享神经网络来估计扰动数据分布的分数函数。 SDEs通过建模正向和反向SDEs实现高效的生成策略。
扩散模型在生成建模任务中取得了显著成果,同时也面临一些限制。未来的研究方向包括进一步探索应用领域、改进计算效率以及提高生成模型的可解释性。
去噪扩散概率模型(DDPMs)
正向过程
在DDPMs中,用 p ( x 0 ) p(x_0) p(x0) 表示原始、未经破坏的训练数据(图像)的概率密度。
概率密度函数描述了在图像空间中每个可能图像的相对概率分布。换句话说, p ( x 0 ) p(x_0) p(x0) 表示了在训练数据集中每个图像出现的概率。
在DDPMs(Denoising Diffusion Probabilistic Models)中, p ( x 0 ) p(x_0) p(x0) 是指模型训练时的初始状态,即未经过任何噪声破坏的原始图像。这个初始状态用于在训练过程中生成具有多样性和质量的图像。模型通过逐步添加高斯噪声来训练,从而逼近或捕捉了训练数据的分布,使其具有一定的鲁棒性和生成能力。
因此, p ( x 0 ) p(x_0) p(x0) 在这里表示模型训练的起点,是学习过程中要模拟的原始图像的概率分布。通过模拟这个概率分布,并在训练中引入逐渐增加的高斯噪声。
给定一个初始状态的训练样本 x 0 ∼ p ( x 0 ) x_0 ∼ p(x_0) x0∼p(x0),通过下面的公式马尔可夫过程获得噪声版本 x 1 、 x 2 . . . , x T x_1、x_2 ...,x_T x1、x2...,xT
p ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t ⋅ x t 1 , β t ⋅ I ) , ∀ t ∈ [ 1 , . . . , T ] p(x_t|x_{t-1}) = N(x_t;\sqrt {1-\beta_t} ·x_{t_1},\beta_t ·I), ∀_t \in [1,...,T] p(xt∣xt−1)=N(xt;1−βt⋅xt1,βt⋅I),∀t∈[1,...,T]
公式解释:
其中 p ( x t ∣ x t − 1 ) p(x_t|x_{t-1}) p(xt∣xt−1) 表示在给定前一步 ( x t − 1 x_{t-1} xt−1) 的条件下,当前步 ( x t x_t xt) 的分布
T T T是扩散步骤的数量, β 1 , . . . , β T ∈ [ 0 , 1 ) β_1, . . . , β_T ∈ [0, 1) β1,...,βT∈[0,1) 是代表扩散步骤中方差变化的超参数, I I I是与输入图像 x 0 x_0 x0具有相同尺寸的单位矩阵,而 N ( x ; µ , σ ) N(x; µ, σ) N(x;µ,σ)表示均值为 µ µ µ和协方差为 σ σ σ的正态分布,产生 x x x。
这个过程可以理解为 x t − 1 x_{t-1} xt−1 分布的基础上,选择一定的均值和方差,在图像 x t − 1 x_{t-1} xt−1 状态下中增加一些正态分布抽样下的噪声。
p ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t ⋅ x t 1 , β t ⋅ I ) , ∀ t ∈ [ 1 , . . . , T ] p(x_t|x_{t-1}) = N(x_t;\sqrt {1-\beta_t} ·x_{t_1},\beta_t ·I), ∀_t \in [1,...,T] p(xt∣xt−1)=N(xt;1−βt⋅xt1,βt⋅I),∀t∈[1,...,T]
上述这个递归公式如果在每一步增加的噪声都是经过均匀的正态分布抽样的话,可以将式子转化为如下:
p ( x t ∣ x 0 ) = N ( x t ; β ^ t ⋅ x 0 , ( 1 − β ^ t ) ⋅ I ) p(x_t|x_0) = N(x_t;\sqrt {\hat \beta_t} ·x_0,(1- \hat \beta_t )·I) p(xt∣x0)=N(xt;β^t⋅x0,(1−β^t)⋅I)
公式解释:
其中 β ^ t = ∏ i = 1 t α i \hat \beta_t=∏_{i=1}^tα_i β^t=∏i=1tαi且 α t = 1 − β t α_t=1−β_t αt=1−βt,基本上式子表示了:如果有原始图像 x 0 x_0 x0并固定方差调度 β t β_t βt,则可以通过单一步骤对任何噪声版本 x t x_t xt进行采样。
前面我们已经知道了如何求在给定前一步 ( x t − 1 x_{t-1} xt−1) 的条件下,当前步 ( x t x_t xt) 的分布,现在要求出本身的图像 x t x_t xt的分布。
这里会用到一个技巧叫重新参数化技巧,通过这个技巧,我们可以从一个标准正态分布 N ( 0 , I ) N(0, I) N(0,I) 中采样样本,并通过线性变换和平移操作,得到原始正态分布 N ( µ , σ 2 ⋅ I ) N(µ, σ² \cdot I) N(µ,σ2⋅I) 中的样本。
这里的标准正态分布 N ( 0 , I ) N(0, I) N(0,I) 对应的是 z t z_t zt,即噪声的分布。原始正态分布 N ( µ , σ 2 ⋅ I ) N(µ, σ² \cdot I) N(µ,σ2⋅I) 对应的是生成的图像 x t x_t xt。
先回顾一下标准正态分布的样本 z ∼ N ( 0 , I ) z \sim N(0, I) z∼N(0,I) 的采样过程:我们从均值为 0,方差为 1 的正态分布中生成一个随机数 z z z。然后,通过乘以标准差 σ σ σ 并加上均值 µ µ µ,我们可以得到原始正态分布 N ( µ , σ 2 ⋅ I ) N(µ, σ² \cdot I) N(µ,σ2⋅I) 中的样本 x x x。这个操作就是重新参数化技巧的基本思想。即:
x = z σ + u x = zσ+u x=zσ+u

其中 u u u就是左边红框的部分, σ σ σ就是右边红框的部分。将它们带入到下面:
x = z σ + u x = zσ+u x=zσ+u
得:
x t = β ^ t ⋅ x 0 + ( 1 − β ^ t ) ⋅ z t x_t = \sqrt{\hat \beta_t}·x_0 +\sqrt{(1-\hat \beta _t)}·z_t xt=β^t⋅x0+(1−β^t)⋅zt
β t β_t βt的属性:为 ( β t ) t = 1 T (\beta_t)_{t=1}^T (βt)t=1T表示方差调度参数,根据论文描述 ( β t ) t = 1 T (\beta_t)_{t=1}^T (βt)t=1T介于 β 1 = 1 0 − 4 和 β T = 2 ⋅ 1 0 − 2 \beta_1=10^{-4}和\beta_T = 2·10^{-2} β1=10−4和βT=2⋅10−2之间其中 T = 1000。
反向过程
DDPMs的反向过程主要涉及如何根据给定的初始样本 x T ∼ N ( 0 , I ) x_T ∼ N(0,I) xT∼N(0,I),按照逆向步骤 p ( x t − 1 ∣ x t ) = N ( x t − 1 ; μ ( x t , t ) , ∑ ( x t , t ) ) p(x_{t-1}|x_t) = N(x_{t-1};μ(x_t ,t),\sum(x_t,t)) p(xt−1∣xt)=N(xt−1;μ(xt,t),∑(xt,t))生成新的样本。
首先,描述一下整个反向生成过程:
- 输入:
-
- T - 扩散步骤的数量。
-
- σ 1 , . . . , σ T σ_1,...,σ_T σ1,...,σT - 反向转换的标准差。
- 输出:
-
- x 0 x_0 x0 - 生成的图像样本。
- 计算过程:
-
- 3.1 从标准正态分布中抽取样本: x T ∼ N ( 0 , I ) x_T∼N(0,I) xT∼N(0,I)。
-
- 3.2 从 T T T步开始逆向迭代直到第 1 步:
-
-
- 如果 t > 1 t>1 t>1,抽取 z ∼ N ( 0 , I ) z∼N(0,I) z∼N(0,I)。
-
-
-
- 否则,令 z = 0 z=0 z=0。
-
-
-
- 计算均值 μ θ μ_θ μθ: μ θ = 1 α t ( x t − 1 − α t 1 − β ^ t ⋅ z θ ( x t , t ) ) μ_θ=\sqrt{\frac{1}{α_t}}(x_t-\sqrt{\frac{1-α_t}{1-\hat \beta_t}}·z_θ(x_t,t)) μθ=αt1(xt−1−β^t1−αt⋅zθ(xt,t))
-
-
-
- 生成样本 x t − 1 x_{t−1} xt−1: x t − 1 = μ θ + σ t ⋅ z x_{t-1} = μ_θ+σ_t ·z xt−1=μθ+σt⋅z
- 生成样本 x t − 1 x_{t−1} xt−1: x t − 1 = μ θ + σ t ⋅ z x_{t-1} = μ_θ+σ_t ·z xt−1=μθ+σt⋅z
-
这个过程通过使用逆向迭代和生成式来产生一个新的样本 x 0 x_0 x0
,它是从 T T T步开始逆向推断过程中生成的最终样本。
噪声条件得分网络(NCSNs)
噪声条件得分网络将数据密度 p ( x ) p(x) p(x)改为相对输入的对数密度的梯度 ∇ x l o g p ( x ) ∇_xlogp(x) ∇xlogp(x)。这些梯度给出的方向被 Langevin 动力学算法定义为用于从随机样本 ( x 0 ) (x_0) (x0) 移动到高密度区域的样本 ( x N ) (x_N) (xN)的方向。
Langevin 动力学是一种受物理学启发的迭代方法,可用于数据采样。在物理学中,该方法用于确定分子系统中粒子的轨迹,允许粒子与其他分子之间发生相互作用。粒子的轨迹受系统的阻力力和由分子之间的快速相互作用引起的随机力的影响。
在算法这里,我们可以将对数密度的梯度视为一种力,将随机样本通过数据空间拖向高数据密度 p ( x ) p(x) p(x) 的区域。
另外用 ω i ω_i ωi表示物理学中的随机力, γ γ γ值表示这两种力的影响,因为它代表粒子所处环境的摩擦系数。
从采样的角度看, γ γ γ控制更新的幅度。
通过训练 NCSNs 模型,我们可以有效地估计给定噪声尺度下的得分。在采样过程中,通过 Annealed Langevin dynamics 过程,模拟粒子在势能场中的运动,从而生成样本。整个框架通过对不同噪声水平下的数据建模,使得模型更具鲁棒性,能够处理数据中的不同特征和模式。
Langevin 动力学的迭代目标函数更新如下:
x i = x i − 1 + γ 2 ∇ x l o g p ( x ) + γ ⋅ w i x_i = x_{i-1}+\frac{γ}{2}∇_xlogp(x)+\sqrt{γ}·w_i xi=xi−1+2γ∇xlogp(x)+γ⋅wi
其中 i ∈ [ 1 , . . . , N ] i \in [1,...,N] i∈[1,...,N], γ γ γ控制更新在得分方向的幅度, x 0 x_0 x0 从先验分布中采样,噪声 w i ∼ N ( 0 , I ) w_i ∼N(0,I) wi∼N(0,I)解决了陷入局部最小值的问题,该方法递归地应用于 N → ∞ N→∞ N→∞步,
因此生成模型可以使用上述方法从 p ( x ) p(x) p(x)中采样,先通过神经网络 s θ ( x ) s_θ(x) sθ(x)估计得分 ∇ x l o g p x ( x ) ∇_xlogpx(x) ∇xlogpx(x)。
该网络可以通过分数匹配进行训练,就需要优化损失函数:
L s m = E x ∼ p ( x ) ∣ ∣ s θ ( x ) − ∇ x l o g p x ( x ) ∣ ∣ 2 2 L_{sm} = E_{x∼p(x)}||s_θ(x) -∇_xlog px(x) ||_2^2 Lsm=Ex∼p(x)∣∣sθ(x)−∇xlogpx(x)∣∣22
正向过程
初始化
给定一个高斯噪声尺度序列 σ 1 < σ 2 < … < σ T σ_1 <σ_2<…<σ_T σ1<σ2<…<σT使得 p σ 1 ( x ) ≈ p ( x 0 ) p_{σ_1}(x)≈p(x _0) pσ1(x)≈p(x0)和 p σ T ( x ) ≈ N ( 0 , I ) p_{σ_T(x)}≈N(0,I) pσT(x)≈N(0,I),
训练 NCSNs
可以使用去噪分数匹配训练一个 NCSN s θ ( x , σ t ) s_θ(x,σ_t) sθ(x,σt),使得 s θ ( x , σ t ) ≈ ∇ x l o g ( p σ t ( x ) ) s_θ(x,σ_t )≈∇_xlog(p_{σ_t}(x)) sθ(x,σt)≈∇xlog(pσt(x)),对于所有 t ∈ [ 1 , . . . , T ] t∈[1,...,T] t∈[1,...,T]。可以推导 ∇ x l o g ( p σ t ( x ) ) ∇_xlog(p_{σ_t}(x)) ∇xlog(pσt(x)) 如下:
∇ x t l o g p σ t ( x t ∣ x ) = − x t − x σ t 2 ∇_x^tlogp_{σ_t}(x_t|x)=-\frac{x_t-x}{σ_t^2} ∇xtlogpσt(xt∣x)=−σt2xt−x
鉴于:
p σ t ( x t ∣ x ) = N ( x t ; x , σ t 2 ⋅ I ) = 1 σ t ⋅ 2 π e x p ( − 1 2 ⋅ ( x t − x σ t ) 2 ) p_{σ_t}(x_t|x)=N(x_t;x,σ_t^2·I)=\frac{1}{σ_t·\sqrt{2π}}exp(-\frac{1}{2}·(\frac{x_t-x}{σ_t})^2) pσt(xt∣x)=N(xt;x,σt2⋅I)=σt⋅2π1exp(−21⋅(σtxt−x)2)
将$ ∇ x l o g ( p σ t ( x ) ) ∇_xlog(p_{σ_t}(x)) ∇xlog(pσt(x))带入到损失函数进行替换,得到如下:

其中, λ ( σ t λ(σ_t λ(σt 是权重函数, p σ t p_{σ_t} pσt是给定噪声尺度 σ t σ_t σt 下的噪声分布。
生成样本
在推断时,采用 Annealed Langevin dynamics 过程生成样本。
反向过程
- 初始化: 使用白噪声生成初始样本 x 0 T ∼ N ( 0 , I ) x_0^T∼N(0,I) x0T∼N(0,I)。
- 迭代更新:从 t = T t=T t=T到 t = 1 t=1 t=1进行迭代,每一步包含 N N N次更新。对于每次更新 i = 1 , … , N i=1,…,N i=1,…,N,进行以下步骤:
-
- 2.1 从标准正态分布 N ( 0 , I ) N(0,I) N(0,I) 中采样噪声项 ω ω ω,即 ω ∼ N ( 0 , I ) ω∼N(0,I) ω∼N(0,I)
-
- 2.2 使用已训练的 NCSNs 模型 s θ ( x i − 1 t , σ t ) s_θ (x_{i−1}^t ,σ_t) sθ(xi−1t,σt) 估计得分。
-
- 2.3 根据 Langevin dynamics 更新规则,计算下一步样本 x i t : x i t = x i − 1 t + γ t 2 s θ ( x i − 1 t , σ t ) + γ t ω x_i^t:x_i^t=x_{i-1}^t +\frac{γ_t}{2}s_θ(x_{i-1}^t,σ_t)+\sqrt{γ_t}ω xit:xit=xi−1t+2γtsθ(xi−1t,σt)+γtω
-
- 2.4 保留每一步更新后的样本 x i t x_i^t xit。
- 返回结果: 返回 x 0 T − 1 x_0^{T−1} x0T−1 ,即最后一步的样本。
最后通过一段文字来解释为什么可以用Langevin 动力学来实现(NCSNs)
当我们试图从一个概率分布中采样样本时,尤其是高维空间中的复杂分布,这个过程可能非常具有挑战性。Langevin 动力学是一种仿照物理学中粒子在势能场中运动的方式的采样方法,这里的 “势能场” 实际上是指我们想要从中采样的概率分布。
想象一下,你是一颗微小的颗粒,漂浮在这个概率分布所定义的空间中。在物理学中,Langevin 动力学通常用于描述微粒在液体或气体中的运动,受到来自环境的阻力和随机碰撞的影响。类似地,在采样过程中,我们将你想象成这个微粒,而概率分布中的梯度(得分)则是指导你朝向高概率区域的力。
Langevin 动力学就像是你在一个由数据密度定义的山谷中滚动。梯度给出了你应该滚动的方向,而随机噪声则模拟了环境的不确定性和波动性。这种动力学确保了你不仅能够向概率分布的高密度区域移动,而且由于随机性,有时你也能够跳出局部最小值。
换句话说,通过仿效物理学中微粒在势场中的运动方式,Langevin 动力学提供了一种直观而生动的方式,使我们能够在概率分布中游走,从而采样到我们感兴趣的样本。在这个过程中,我们借助神经网络(NCSNs)来模拟概率分布的梯度,使得我们能够更有效地引导采样过程,特别是在处理不同噪声水平和复杂数据模式时。
随机微分方程(SDEs)
原理背景
随机微分方程(SDEs)方法类似于前述方法,如DDPMs和NCSNs,旨在通过将数据分布逐渐转化为噪声来进行采样。这种方法的独特之处在于它将扩散过程视为连续的,从而成为随机微分方程的解。具体而言,该方法在生成过程中使用了正向扩散SDE和逆向扩散SDE。正向扩散过程模拟了从初始数据分布 p ( x 0 ) p(x_0) p(x0)逐渐过渡到噪声的过程。
正向过程
正向扩散过程的SDE表达式为:
∂ t ∂ x = f ( x , t ) + σ ( t ) ⋅ ω t \frac{∂t}{∂x}=f(x,t)+σ(t)⋅ω_t ∂x∂t=f(x,t)+σ(t)⋅ωt
其中, ω t ω_t ωt是高斯噪声, f f f是计算漂移系数的函数, σ σ σ是计算扩散系数的时间相关函数。这个过程的目标是通过设计漂移系数,逐渐减小数据 x 0 x_0 x0,同时通过扩散系数控制添加的高斯噪声的程度。
反向过程
与正向过程对应的逆向SDE表示为:
∂ t ∂ x = f ( x , t ) − σ ( t ) 2 ⋅ ∇ x l o g p t ( x ) ⋅ ∂ t + σ ( t ) ⋅ ∂ ω \frac{∂t}{∂x} =f(x,t)− \frac{σ(t)}{2} ⋅∇xlogp_t (x)⋅∂t+σ(t)⋅∂ω ∂x∂t=f(x,t)−2σ(t)⋅∇xlogpt(x)⋅∂t+σ(t)⋅∂ω
反向过程的关键在于逐步去除导致数据破坏的漂移项。这是通过减去 σ ( t ) 2 ⋅ ∇ x l o g p t ( x ) \frac{σ(t)}{2}·∇x log p_t(x) 2σ(t)⋅∇xlogpt(x)来实现的。
模型训练与采样
为了实现这一过程,Song等人的生成模型利用神经网络估计得分函数,通过数值SDE求解器从 p ( x 0 ) p(x_0) p(x0)生成样本。神经网络 s θ ( x , t ) s_θ(x, t) sθ(x,t)接收扰动数据和时间步长作为输入,并生成对得分函数的估计。
训练时,使用了连续情况下的目标函数:
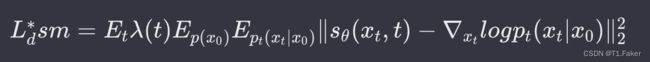
其中,λ是权重函数, t ∼ U ( [ 0 , T ] ) t ∼ U([0, T]) t∼U([0,T])。
采样方法
采样过程采用Euler-Maruyama采样方法,通过数值方法求解逆向SDE。在实践中,数值求解器通常不适用于连续公式,因此使用了Euler-Maruyama方法,通过固定微小负步长 Δ t \Delta t Δt执行采样过程。采样过程中的布朗运动由 Δ ω ^ = ∣ Δ t ∣ ⋅ z \Delta \hat{ω} = \sqrt{|\Delta t|} · z Δω^=∣Δt∣⋅z给出,其中 z ∼ N ( 0 , I ) z ∼ N(0, I) z∼N(0,I)。
方法可行性解释
该方法的可行性在于通过对数据密度的漂移和扩散过程的连续建模,成功地将数据逐渐转化为噪声。神经网络的引入提高了模型的表达能力,使其能够学习和逼近复杂的分布。采样过程中的数值方法确保了实际可行性,并通过改进的采样技术进一步提高了样本的质量。整体而言,该方法通过巧妙的数学建模和神经网络的结合,成功地实现了高质量样本的生成。
