离散信号的卷积与相关

这里的相关是指互相关。

1.一维离散信号的卷积与相关

计算模式为"full"。

卷积：
$f(t)\ast g(t)=\sum _{\tau =-\infty }^{\infty }f(\tau ).g(t-\tau )$
相关：
$f(t)\otimes g(t)=\sum _{\tau =-\infty }^{\infty }f(\tau ).g(t+\tau )$

从公式来看，卷积和相关都是两个信号对应位置元素的积之和。

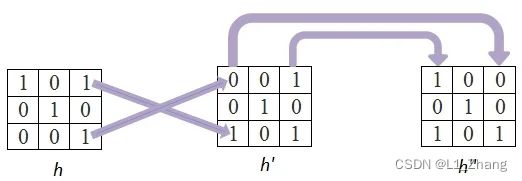
不同的是，卷积运算将卷积核顺序进行了反向。

举个例子：

$f$为离散序列[1,2,3,4]，$g$为离散序列[1,2,3]，

卷积计算：

$f(0)\ast g(0)=f(0)\times g(0)=1\times 1=1$
$f(1)\ast g(1)=f(0)\times g(1)+f(1)\times g(0)=1\times 2+2\times 1=4$
$f(2)\ast g(2)=f(0)\times g(2)+f(1)\times g(1)+f(2)\times g(0)=1\times 3+2\times 2+3\times 1=10$
$f(3)\ast g(3)=f(1)\times g(2)+f(2)\times g(1)+f(3)\times g(0)=2\times 3+3\times 2+4\times 1=16$
$f(4)\ast g(4)=f(2)\times g(2)+f(3)\times g(1)=3\times 3+4\times 2=17$
$f(5)\ast g(5)=f(3)\times g(2)=4\times 3=12$

即结果为[1,4,10,16,17,12]。

互相关计算：

互相关的"full"模式计算，两边要先pad 个数为 k-1的0。k为核序列的长度。

$f$为离散序列[1,2,3,4]，pad 0 后为[0,0,1,2,3,4,0,0]。

计算过程为：

$f(0)\otimes g(0)=f(0)\times g(0)+f(1)\times g(1)+f(2)\times g(2)=0\times 1+0\times 2+1\times 3=3$
$f(1)\otimes g(1)=f(1)\times g(0)+f(2)\times g(1)+f(3)\times g(2)=0\times 1+1\times 2+2\times 3=8$
$f(2)\otimes g(2)=f(2)\times g(0)+f(3)\times g(1)+f(4)\times g(2)=1\times 1+2\times 2+3\times 3=14$
$f(3)\otimes g(3)=f(3)\times g(0)+f(4)\times g(1)+f(5)\times g(2)=2\times 1+3\times 2+4\times 3=20$
$f(4)\otimes g(4)=f(4)\times g(0)+f(5)\times g(1)+f(6)\times g(2)=3\times 1+4\times 2+0\times 3=11$
$f(5)\otimes g(5)=f(5)\times g(0)+f(6)\times g(1)+f(7)\times g(2)=4\times 1+0\times 2+0\times 3=4$

即结果为[3,8,14,20,11,4]。

1.1 scipy实现

import numpy as np
from scipy import signal
sig = np.arange(1,5)
kernel = np.array([1,2,3])

卷积

signal.convolve(sig, kernel, mode='full')
# array([ 1,  4, 10, 16, 17, 12])

相关

signal.correlate(sig, kernel, mode='full')
# array([ 3,  8, 14, 20, 11,  4])

1.2 个人Python实现

def convolve1D(signal,kernel,mode='full'):
    K=len(kernel)
    kernel=kernel[::-1]
    out=[]
    if mode=="full":
        pad=K-1
        signal2=np.pad(signal,pad_width=pad)
        for i in range(K,len(signal2)+1):
            out.append(np.sum(signal2[i-K:i]*kernel))
    return np.array(out)
    
sig = np.arange(1,5)
kernel = np.array([1,2,3])
out = convolve1D(sig,kernel)
# array([ 1,  4, 10, 16, 17, 12])

1.3 一维卷积与相关的关系

将卷积核进行反向，再与信号相关运算，得到了卷积运算的结果。

signal.correlate(sig, kernel[::-1], mode='full')
# array([ 1,  4, 10, 16, 17, 12])

对于相关运算，也有相同的结论。

signal.convolve(sig, kernel[::-1], mode='full')
# array([ 3,  8, 14, 20, 11,  4])

因此，我们只要有相关和卷积其中一种算子，就可以进行这两种运算了。

同时也会有，如果卷积核是对称的，卷积和相关结果一致。

kernel = np.array([1,2,1])

signal.convolve(sig, kernel, mode='full')
# array([ 1,  4,  8, 12, 11,  4])

signal.correlate(sig, kernel, mode='full')
# array([ 1,  4,  8, 12, 11,  4])

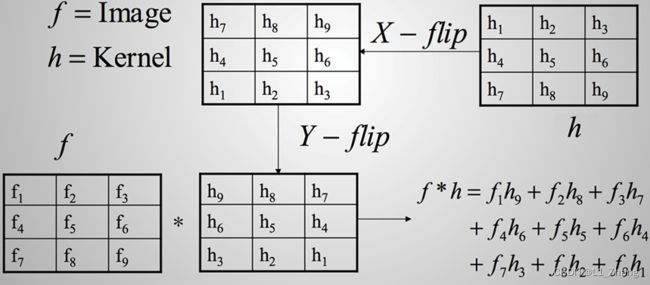
2.二维离散信号的卷积与相关

讨论了一维信号卷积和相关的运算及其性质，也可以类推到二维的情况。

这里不再举例验证，只给出一般性的公式，然后通过将卷积核矩阵反转的方式进行相关运算。

卷积：
$(f\ast g)[m,n]=\sum _{i=-\infty }^{\infty }\sum _{j=-\infty }^{\infty }f[i,j]\cdot h[m-i,n-j]$

相关：
$(f\otimes g)[m,n]=\sum _{i=-\infty }^{\infty }\sum _{j=-\infty }^{\infty }f[i,j]\cdot h[m+i,n+j]$

对于一维情况，模式为"full"。这里选择"same"模式，即卷积前后，数据大小不变。

2.1 二维卷积运算的scipy与个人Python实现

2.1.1 pad 0

import numpy as np
from scipy import signal

def Convolve2D(img, kernel,pad=None):    
    kernel=np.flipud(np.fliplr(kernel)) #卷积核反转
    h_k,w_k = kernel.shape   
    h_img,w_img = img.shape
    if pad is None:
        pad=(h_k-1)//2
    if pad != 0:         
        img_pad = np.zeros((img.shape[0] + pad*2, img.shape[1] + pad*2),dtype=np.float64)      
        img_pad[int(pad):int(-1 * pad), int(pad):int(-1 * pad)] = img      
    else:
        img_pad = img      
    
    out = np.zeros((h_img, w_img),dtype=np.float64)
    for y in range(img.shape[1]):          
            for x in range(img.shape[0]):            
                    out[x, y] = np.sum(kernel * img_pad[x: x + h_k, y: y + w_k])   
 
    return out

img=np.arange(25).reshape(5,5)
kernel=np.random.randint(0,5,(3,3)).astype(float)
a=Convolve2D(img, kernel)


b=signal.convolve(img, kernel,mode='same')
# convolve2d(img, kernel,mode='same')


print(a)
# [[  3.  23.  34.  45.  41.]
#  [ 30.  82.  99. 116.  93.]
#  [ 65. 167. 184. 201. 153.]
#  [100. 252. 269. 286. 213.]
#  [135. 262. 276. 290. 189.]]
print(b)
# [[  3.  23.  34.  45.  41.]
#  [ 30.  82.  99. 116.  93.]
#  [ 65. 167. 184. 201. 153.]
#  [100. 252. 269. 286. 213.]
#  [135. 262. 276. 290. 189.]]

运算过程见下图：

再通过下图感受下卷积核反转的过程：

另外,为保持数据尺寸不变，需要在数据四周进行pad，默认为0。

由$O=\frac{i-k+2p}{s}+1$，s取1，且 $i=O$，所以 $p=\frac{k-1}{2}$。

2.1.2 不需要pad 0

不进行pad，实现卷积前后，矩阵尺寸不变。

def Convolve2D_noPad(img, kernel):    
    kernel=np.flipud(np.fliplr(kernel)) #卷积核反转
    h_k,w_k = kernel.shape   
    h_img,w_img = img.shape
    out = np.zeros((h_img, w_img),dtype=np.float64)
    for x in range(h_img):              
        for y in range(w_img):          
                intens = 0.0
                for i in range(h_k):
                    for j in range(w_k):
                        curRow = x - h_k // 2 + i
                        curCol = y - w_k // 2 + j
                        curRow = row + ks // 2 - i
                        curCol = col + ks // 2 - j                        
                        if (0 <= curRow < h_img and 0 <= curCol < w_img):
                            value = img[curRow,curCol]
                            intens += value * kernel[i,j]
                out[x, y] = intens

    return out

另外也可以不反转卷积核：

def Convolve2D_noPad(img, kernel):    
    h_k,w_k = kernel.shape   
    h_img,w_img = img.shape
    out = np.zeros((h_img, w_img),dtype=np.float64)
    for x in range(h_img):              
        for y in range(w_img):          
                intens = 0.0
                for i in range(h_k):
                    for j in range(w_k):
                        curRow = row + ks // 2 - i
                        curCol = col + ks // 2 - j                        
                        if (0 <= curRow < h_img and 0 <= curCol < w_img):
                            value = img[curRow,curCol]
                            intens += value * kernel[i,j]
                out[x, y] = intens

    return out

## 2.2 二维相关运算的scipy与个人Python实现
把卷积核反转这一步去掉,卷积运算就回到了相关运算。

```python
    kernel=np.flipud(np.fliplr(kernel)) #卷积核反转

完整代码如下：

import numpy as np
from scipy import signal


def Correlate2D(img, kernel,pad=None):    
    h_k,w_k = kernel.shape   
    h_img,w_img = img.shape
    if pad is None:
        pad=(h_k-1)//2
    if pad != 0:         
        img_pad = np.zeros((img.shape[0] + pad*2, img.shape[1] + pad*2),dtype=np.float64)      
        img_pad[int(pad):int(-1 * pad), int(pad):int(-1 * pad)] = img      
    else:
        img_pad = img      
    
    out = np.zeros((h_img, w_img),dtype=np.float64)
    for y in range(img.shape[1]):          
            for x in range(img.shape[0]):            
                    out[x, y] = np.sum(kernel * img_pad[x: x + h_k, y: y + w_k])   
 
    return out

img=np.random.randint(0,5,(5,5)).astype(float)
kernel=np.random.randint(0,5,(3,3)).astype(float)
a=Correlate2D(img, kernel)
b=signal.correlate2d(img, kernel,mode='same')


print(a)
# [[40. 54. 48. 47. 26.]
#  [44. 49. 63. 63. 45.]
#  [20. 38. 50. 61. 46.]
#  [28. 49. 48. 66. 44.]
#  [20. 35. 44. 44. 30.]]
print(b)
# [[40. 54. 48. 47. 26.]
#  [44. 49. 63. 63. 45.]
#  [20. 38. 50. 61. 46.]
#  [28. 49. 48. 66. 44.]
#  [20. 35. 44. 44. 30.]]

下图为CNN卷积运算，妥妥的相关，但是又因为相关和卷积运算难舍难分的联系，叫卷积也算OK。

参考文献

[1] CS131专题-1：卷积、互相关
[2] 2D Convolution in Image Processing