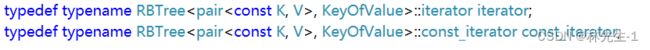【C++笔记】红黑树封装map和set
一、map和set的泛型封装逻辑
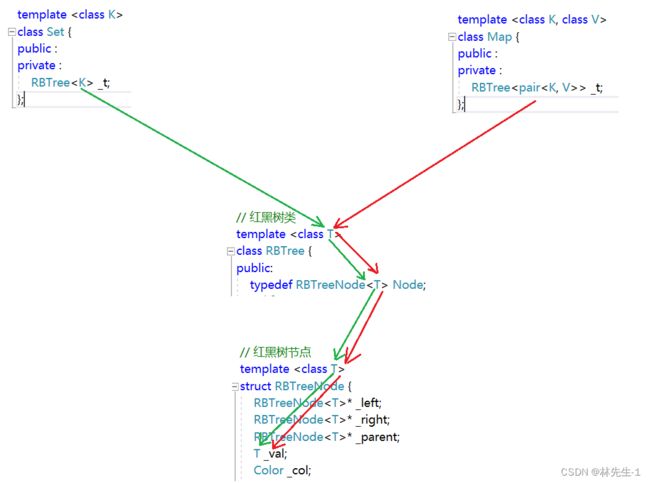
map和set的底层都是红黑树,所以我们想要用红黑树封装map和set的第一个问题就来了,因为set是key结构而map是key-value结构,怎样用同一个底层结构去封装出两个不同存储结构的容器呢?难道我们要将红黑树的代码复制两份,然后针对性的修改代码吗?
其实并不需要,因为C++有模板啊,我们可以借助C++的模板来帮我们完成一个泛型封装,简单来说就是map和set在上层将底层红黑树所需要存储的数据以模板参数的形式传给底层的红黑树。
具体逻辑如下图:
在上层set和map分别传给红黑树的是K和pair
代码:
// Set
template
class Set {
public :
private :
RBTree _t;
};
// Map
template
class Map {
public :
private :
RBTree> _t;
};
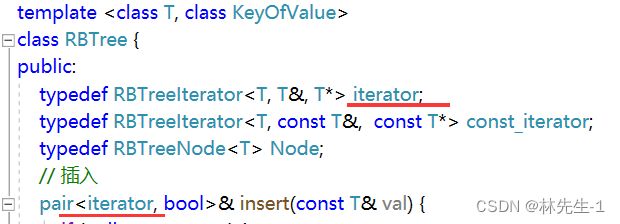
// 红黑树类
template
class RBTree {
public :
typedef
RBTree Node;
private :
Node _root;
};
// 红黑树节点
template
struct RBTreeNode {
RBTreeNode* _left;
RBTreeNode* _right;
RBTreeNode* _parent;
T _val;
Color _col;
// 构造
RBTreeNode(const T& val)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _val(val)
, _col(RED) // 新增节点要给红色
{}
};
二、插入中值比较的解决方法
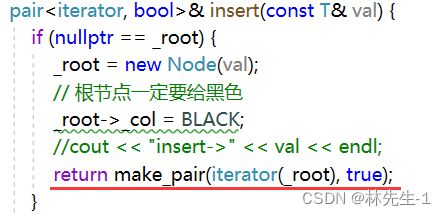
解决了第一个问题,我们就可以实现map和set的插入了,我们知道当下层已经实现了插入逻辑后,上层实现的插入逻辑是很简单的,只需要复用下层的插入即可。
好像这样确实已经可以了,但是我们不能忽略了一个重要的问题,map中存的是一个键值对pair,而我们在插入或查找的时候进行比较都是只针对pair中的K的,也就是pair中的first成员,那pair本身重载的比较方法是否也是只针对fist呢?
我们可以先去查查文档:
查看文档后我们就会发现,pair本身重载的比较方法并不是只针对与first的,它是first和second都会比较到。
所以,如果只用pair原来的比较方法在插入或者是查找的时候就可能出现问题了,所以我们要想个办法统一一下比较方法。
因为pair库中的一个结构,所以我们并不能到它内部去重载它的比较方法,所以我们就需要“提取”出它的first成员。
我们可以创建一个仿函数来做到这个事情,这是因为仿函数也称为函数对象,它是可以作为模板参数传到下层的红黑树的,比较方便。
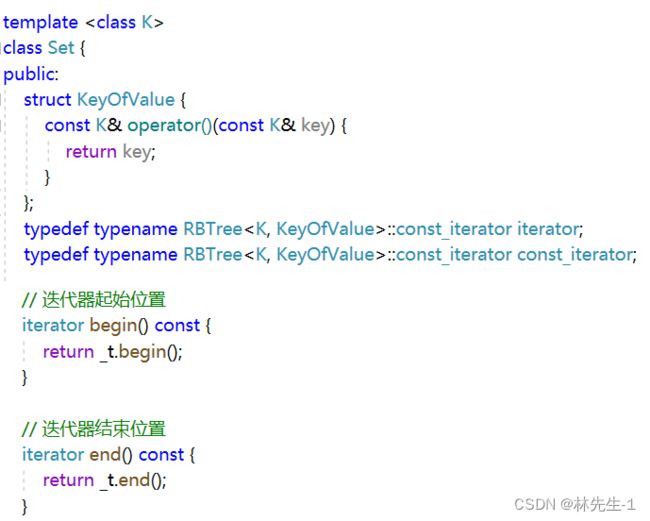
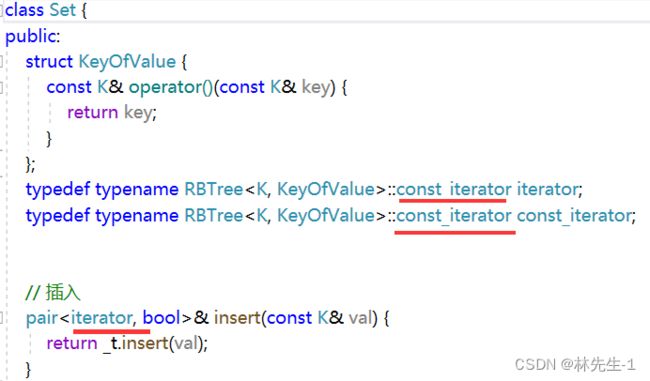
为了统一,Set和Map都需要一个仿函数,然后传给红黑树:
但是对于Set来说这个KeyOfValue只是走走过场而已,因为它本身就只存储了一个K,完全只是为了配合Map。
然后我们就只需要在所有涉及到值比较的地方套上这个仿函数就能解决问题了:
代码:
// Set
struct KeyOfValue {
K& operator()(const K& key) {
return key;
}
};
// Map
struct KeyOfValue {
K& operator()(const pair& kv) {
return kv.first;
}
}; 这样我们就可以放心的完成Map和Set的插入逻辑了:
// Map插入
bool insert(const pair& kv) {
return _t.insert(kv);
}
// Set插入
bool insert(const K& val) {
return _t.insert(val);
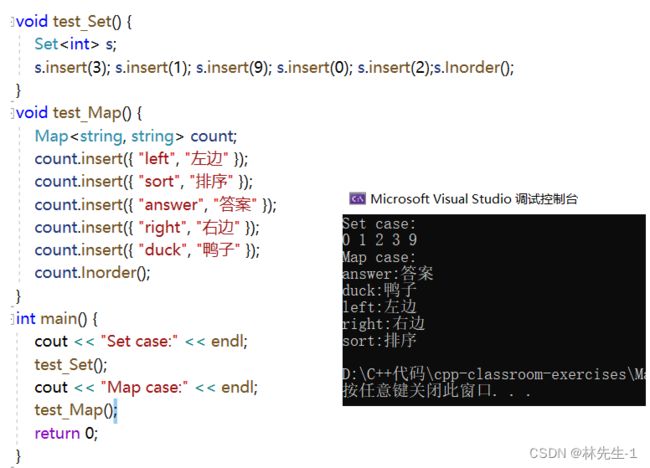
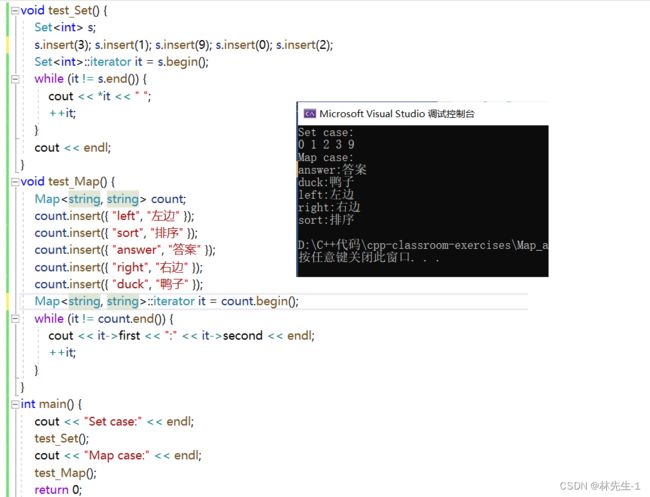
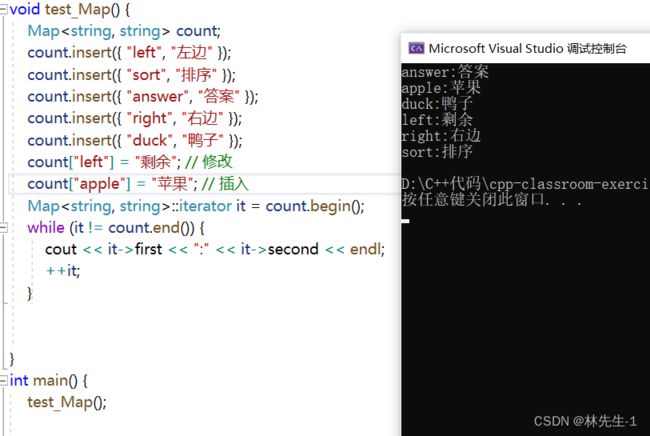
} 我们也可以临时写一个中序遍历来试验一下:
三、迭代器的实现
然后我们就需要来实现我们容器必须的迭代器了,其实树形结构的迭代器和链表结构的迭代器是一样的,都是创建一个迭代器类然后封装一个节点指针,只是在迭代器向后何向前移动的时候实现逻辑不同而已:
// 红黑树迭代器类
template
class RBTreeIterator {
typedef RBTreeNode Node;
typedef RBTreeIteraotr iterator;
public :
// 构造
RBTreeIterator(Node* node)
:_node(node)
{}
// 星号解引用
T& operator*() {
return _node->_val;
}
// 箭头解引用
T* operator->() {
return &_node->_val;
}
// 不等于
bool operator!=(const iterator& it) {
return _node != it._node;
}
// 前置++
iterator& operator++() {
// ……
}
// 前置--
iterator& operator--() {
// ……
}
private :
Node* _node;
}; 3.1、迭代器++的实现
然后我们就要来实现迭代器最主要的功能——++操作。
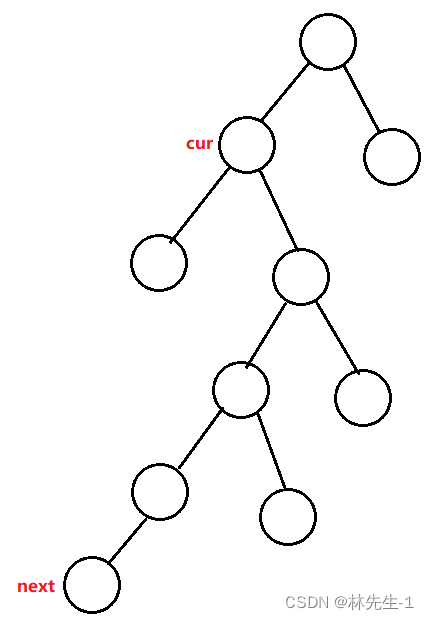
迭代器其实就是根据二叉树的中序遍历来走的,所以我们一开始来找迭代开始的第一个节点,也就是找begin,就是要找到中序遍历的第一个位置。
根据中序遍历的规则我们很容易知道中序遍历的第一个位置就是二叉树中最左的那个节点,所以我们红黑树的begin的实现逻辑就如下:
// 迭代器开始位置
iterator begin() {
Node* cur = _root;
// 找到最左节点
while (cur && cur->_left) {
cur = cur->_left;
}
// 返回使用迭代器的构造即可
return iterator(cur);
}然后结束位置,我们给个空就就行了,因为最后遍历完都会遍历到空:
// 迭代器结束位置
iterator end() {
return iterator(nullptr);
}那我们又怎么从起始位置走到下一个位置呢?我们首先来分析一下中序遍历的逻辑:
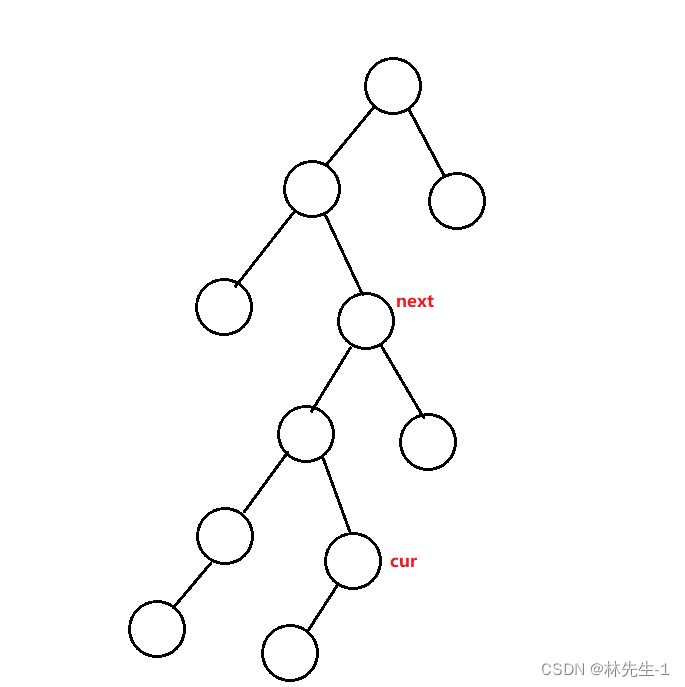
我们知道中序遍历的顺序是“左中右”,并且是递归的形式进行的,所以对于每一个节点都会先去遍历它的左子树。由此我们就能得到一个结论:只要当前节点被遍历到那么要么是它没有左子树要么就是它的左子树已经被遍历完了。
所以,如果当前节点的右子树不为空的话。接下来就要遍历到右子树了,而右子树的遍历又是递归“左中右”的形式,所以当前节点的下一个节点就是右子树的最左节点。
这是第一种情况。
那第二种情况就是右子树为空的情况,这个情况该怎么分析呢?
我们还是要紧紧抓住“递归”这个特性,递归的遍历顺序是“左中右”,所以一定是先遍历根节点再遍历右子树,且父亲的左子树也一定是被遍历完的啦,所以这种情况我们一定是“往回走”。
由上分析可知,如果当前节点是其父亲的右子树的话,那么它的父亲节点也一定被遍历过的了。同理在向上走的过程中,只要遇到当前节点是其父亲的右孩子的情况,其父亲也一定是被遍历过的,只有遇到当前节点是其父亲的左的情况,才说明其父亲是没有被遍历过的。
所以结论是:如果当前节点的右子树为空的话,那么它的下一个节点则是向上寻找到的第一个孩子为父亲左的父亲节点。
所以我们迭代器前置++的代码也就出来了:
// 前置++
iterator& operator++() {
assert(_node != nullptr);
if (_node->_right) { // 如果右不为空,就去寻找右子树的最左节点
Node* cur = _node->_right;
while (cur->_left) {
cur = cur->_left;
}
_node = cur;
}
else { // 如果为空,就向上寻找第一个孩子为父亲左的父亲节点
Node* cur = _node;
Node* parent = cur->_parent;
while (parent&& cur = parent->_right) { // 有可能会走到根,所以parent有可能为空
cur = parent;
parent = cur->_parent;
}
_node = parent;
}
return *this;
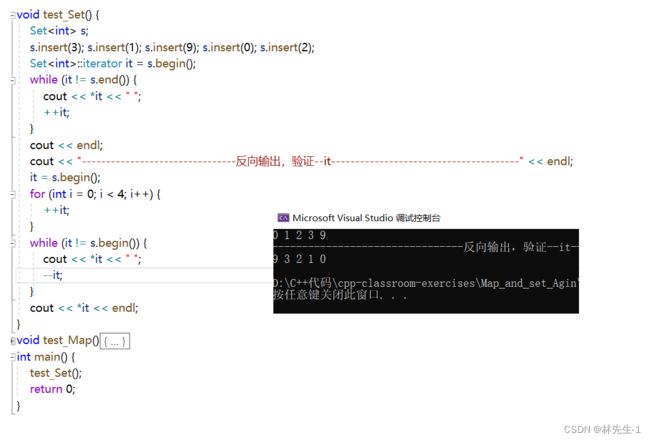
}写完我们可以简单得来测试一下:
3.2、迭代器--的实现
迭代器的--操作我觉得都不用讲了,完全是++反过来就行了,没错!只需要修改一下方向即可。
其实如果要推原理的话也只是和++反方向而已,将遍历方向换成“右中左”像上面++一样的逻辑去推就行了:
// 前置--
iterator& operator--() {
assert(nullptr != _node);
if (_node->_left) { // 如果左不为空就去找左子树的最右节点
Node* cur = _node->_left;
while (cur->_right) {
cur = cur->_right;
}
_node = cur;
}
else { // 如果左为空,就去向上去找第一个孩子为父亲右的父亲节点
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_left) {
cur = parent;
parent = cur->_parent;
}
_node = parent;
}
return *this;
}为了证明这样是可行的,我还是来测试一下吧:
四、const迭代器的实现
const迭代器也是和链表的一样,不需要再复制一份代码,只需要套一层模板即可:
// 红黑树迭代器类
template
class RBTreeIterator {
typedef RBTreeNode Node;
typedef RBTreeIterator iterator;
public :
// 构造
RBTreeIterator(Node* node)
:_node(node)
{}
// 星号解引用
Ref operator*() {
return _node->_val;
}
// 箭头解引用
Ptr operator->() {
return &_node->_val;
}
// 不等于
bool operator!=(const iterator& it) {
return _node != it._node;
}
// 前置++
iterator& operator++() {
assert(_node != nullptr);
if (_node->_right) { // 如果右不为空,就去寻找右子树的最左节点
Node* cur = _node->_right;
while (cur->_left) {
cur = cur->_left;
}
_node = cur;
}
else { // 如果为空,就向上寻找第一个孩子为父亲左的父亲节点
Node* cur = _node;
Node* parent = cur->_parent;
while (parent&& cur == parent->_right) { // 有可能会走到根,所以parent有可能为空
cur = parent;
parent = cur->_parent;
}
_node = parent;
}
return *this;
} 下一步,给红黑树加上const迭代器:
4.1、解决不能修改的问题
其实Set是不分什么const和非const迭代器,因为它里面就只存了一个K,并且是绝对不能修改的,但是为了完整性,我们还是得搞出const和非const迭代器出来。
所以它的const和非const迭代器虽然名字不同,但底层都是const迭代器,写出来就是这样子:
并且在特原本实现的begin和end后面再加上const修饰即可。
这样我们再想去修改Set中的值就会出错了:
而对于Map,我们是想让它的V可以修改,而K不能修改,所以Map需要分const和非const迭代器,但不管是const或非const迭代器,都不能修改K。
所以我们可以在传递模板参数的时候就解决,K不能被修改的问题,只需要将模板参数中的K修改成const K即可:
并且在迭代器的声明处也需要加上const,不然的话类型是对不上的:
还要再加上const和非const的begin和end:
这样子,我们再想去修改K的时候就会报错:
而V是可以修改的:
但是关于迭代器的问题问题还没有完,因为Map还要实现一个方括号运算符重载,这个重载能做到插入或者修改V,在实现这个重载的时候,还会跳出来一个更加麻烦的问题。
4.2、实现Map的方括号运算符重载
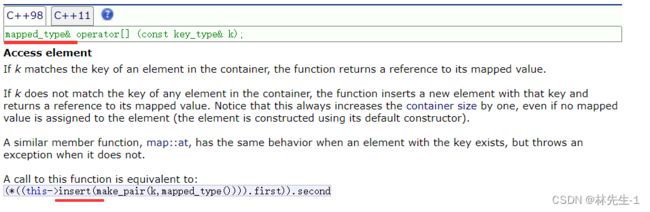
我们先来查查文档,看看Map中的方括号具体的实现形式是怎样的:
其实看不懂不要就,我们主要是想提取出里面的关键信息,从下方画横线处我们可获悉它的实现是借助inser来实现的。
然后返回值看不懂我们就来看看它对返回值的描述:
所以我们明白了,方括号的返回值就是V的引用。
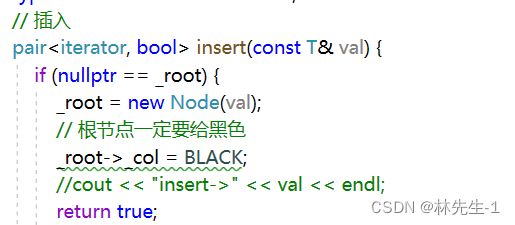
同时为了实现从insert的返回值中提取出V我们还要修改insert的返回值。
将insert的返回值从bool修改成pair
因为上面就符合上面的逻辑了。
而且在所有返回的地方也要进行修改:
所以方括号的实现逻辑就是从insert的返回值中提取出V,反正它插入成功或失败都会返回一个pair:
// 方括号运算符重载
V& operator[](const K& key) {
pair ret = insert(make_pair(key, V()));
return ret.first->second;
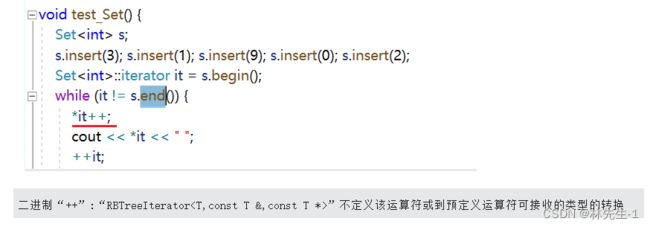
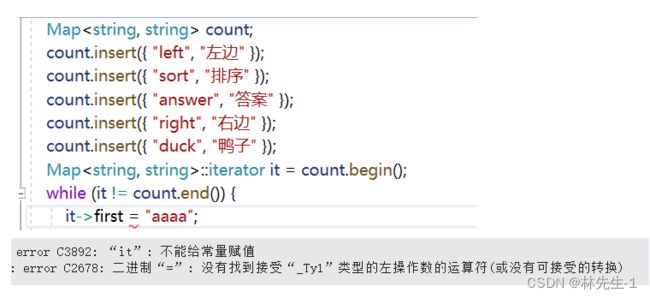
} 但是还没有完成,当我们一编译就会发现一个很严重的问题:
![]()
4.3、解决const和非const迭代器的转化问题
为什么会出现上面的这种问题呢?
其实问题就出在我们将insert的返回值修改成pair
而在Set中只有const迭代器:
所以在红黑树的insert返回给Set的insert的时候就会产生类型转换,而iterator和const_iterator是两种不同的类型,const_iterator的本质其实是其包含的内容不能修改,并不是iterator本身不能修改。
就比如const int *p和int * const p的区别,前者是指针p指向的内容不能修改,后者是指针本身不能修改。const_iterator就相当于前者,所以iterator和const_iterator是两种不同的类型,并不是权限的放大缩小这么简单。
这个问题 其实有一个很巧妙的方法,我们只将红黑树的insert的返回值由pair
纠错!:前面的图中insert给的返回值是引用的形式,其实是不能是引用的,因为有了引用就没拷贝了,这个方法其实就是通过pair的拷贝构造来优化的,用引用的话就失效了。
这个解决方法其实是利用了pair的写得妙的构造函数来实现的:
这其实是一个带模板参数的构造函数,其实这样设计可以做到将构造和拷贝构造合为一体,因为拷贝构造是一定用相同类型的参数来构造的,所以当U和V与要被构造的对象的U和V一样的话,那这就是一个拷贝构造,如果不一样,那就是一个构造。只需要参数里的UV能构造要被构造的对象的UV即可。
而我们这里的pair
所以pair
不得不说,一切都因为pair的这个构造写得实在太好了。
至此,我们的程序就可以正常运行了: