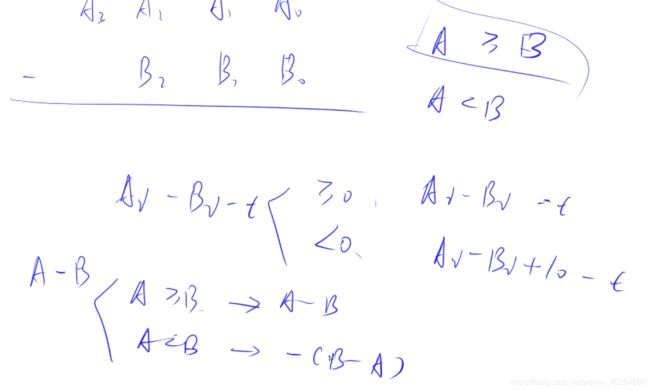算法基础(2) | 高精度、前缀和、差分

一、高精度

1.1 高精度加法

#include 
#include 

using namespace std;

const int N = 1e6 + 10;

vector<int> add(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    
    int t = 0; // 进位
    
    for (int i = 0; i < A.size() || i < B.size(); i ++ )
    {
        if (i < A.size()) t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    
    if (t) C.push_back(1);
    
    return C;
}

int main()
{
    string a, b; //将长度太长的数字 以字符串读入
    vector<int> A, B;//大整数A 和 B 以数组形式存在
    
    cin >> a >> b;   //a = "123456"
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0'); // A = [6,5,4,3,2,1]
    for (int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');
    
    
    auto C = add(A, B);
    
    for (int i = C.size() - 1; i >= 0; i -- ) printf("%d",C[i]);    
    
    return 0;
}

vector<int> add(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    
    int t = 0;//进位
        
    if (A.size() < B.size()) return add(B, A);
    
    for (int i = 0; i < A.size(); i ++ )
    {
        t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
        
        if (t) C.push_back(1);
    }
    
    return C;
}

1.2 高精度减法

#include 
#include 

using namespace std;

const int N = 1010;

// A >= B?
bool cmp(vector<int> &A, vector<int> &B)
{
    if (A.size() != B.size())   return A.size() > B.size(); //直接比较长度长度大的大
    for (int i = A.size() - 1; i >= 0; i -- )   // 长度相等情况下a 不等于 b的情况
        if (A[i] != B[i])
            return A[i] > B[i];
    return true; // a  == b的情况
}

vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    
    int t = 0; //表示借位
    
    for (int i = 0; i < A.size(); i ++ )
    {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        
        if (t < 0) t = 1;
        else t = 0;
    }
    //去除前导0
    
    while (C.size() > 1 && C.back() == 0)   C.pop_back();
    
    return C;
}

int main()
{
    string a, b;
    vector<int> A, B;
    
    cin >> a >> b;
    
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
    for (int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');
    
    if (cmp(A, B))
    {
        vector<int> C = sub(A, B);
        for (int i = C.size() - 1; i >= 0; i -- )   printf("%d",C[i]);
    }else
    {
        vector<int> C = sub(B, A);
        printf("-");
        
        for (int i = C.size() - 1; i >= 0; i -- )   printf("%d",C[i]);
    }
    
    return 0;
}

1.3 高精度乘法

#include 
#include 

using namespace std;

vector<int> mul(vector<int> &A, int b)
{
    vector<int> C;
    
    int t = 0;
    for (int i = 0; i < A.size() || t; i ++ )
    {
        t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
        
    }
    return C;
}

int main()
{
    string a;
    int b;
    vector<int> A;
    
    cin >> a >> b;
    
    for (int i = a.size() - 1; i >= 0; i -- )  A.push_back(a[i] - '0');
    
    vector<int> C = mul(A, b);
    
    for (int i = C.size() - 1; i >= 0; i -- ) printf("%d",C[i]);
    
    
    return 0;
}

1.4 高精度除法

#include 
#include 
#include 
#include 
#include 

using namespace std;

const int N = 1e6 + 10;

//A/b 商是C 余数是r
vector<int> div(vector<int> &A, int b, int & r)
{
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i--)
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(),C.end());
    while(C.size() > 1 && C.back() == 0) C.pop_back();
    
    return C;
}


int main()
{
    string  a;
    int b;
    vector<int> A;
    
    cin >> a >> b;
    for ( int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    
    int r;
    auto C = div(A, b, r);
    
    for (int i = C.size() - 1; i >= 0; i--) printf("%d",C[i]);
    cout << endl << r << endl;
    
}

高精度汇总篇

二、前缀和

2.1 一维前缀和

核心思想：

从1开始的好处，处理边界问题，如要求[1,10]这段和的话，之间s10即可。因为s[0] = 0；

#include 
using namespace std;

const int N = 100010;

int a[N], s[N];

int main()
{
    int n, m;
    ios::sync_with_stdio(false);
    //原理是让cin和标准输入输出不同步 提高cin读取速度
    //副作用不能用scanf了 数据规模大于等于100w建议用scanf 否则用cin即可
    
    cin >> n >> m;
    
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i];
    while (m -- )
    {
        int l, r;
        cin >> l >> r;
        cout << s[r] - s[l - 1] << endl;
    }
        
    return 0;
}

2.2 二前缀和

核心思想：

#include 

using namespace std;

const int N = 1010;

int a[N][N];
int s[N][N];

int main()
{
    int n, m, q;
    
    cin >> n >> m >> q;
    
    //读入数组
    for (int i = 1; i <= n; i ++ )  
        for (int j = 1; j <= m; j ++ ) 
            cin >> a[i][j];
        
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
    
    while (q -- )
    {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        
        cout << s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1] << endl;  
    }
    
    return 0;
}

都是从左上到右下。

三、差分

3.1 一维差分

#include 

using namespace std;

const int N = 100010;

int a[N], b[N];
int n, m;

void insert(int &l, int &r, int &c)
{
    b[l] += c;
    b[r + 1] -= c;
}
int main()
{
    scanf("%d%d", &n, &m);
    
    //读入数据
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    
    //进行构造b数组
    for (int i = 1; i <= n; i ++ ) insert(i, i, a[i]);
    
    // for (int i = 1; i <= n; i ++ ) cout << b[i] << ' ';
    
    while (m -- )
    {
        int l, r, c;
        scanf("%d%d%d", &l, &r, &c);
        insert(l, r, c);
    }
    
    //求原数组
    for (int i = 1; i <= n; i ++ ) b[i] += b[i - 1];
    
    //输出原数组
    for (int i = 1; i <= n; i ++ ) printf("%d ", b[i]);
    
    return 0;
}

#include 
using namespace std;

const int N = 1010;

int a[N], b[N];

int n, m;

int main()
{
    cin >> n >> m;
    
    for (int i = 1; i <= n; i ++ )  cin >> a[i];
    
    for (int i = 1; i <= n; i ++ )  b[i] = a[i] - a[i - 1];
    
    while (m -- )
    {
        int l, r, c;
        cin >> l >> r >> c;
        b[l] += c;
        b[r + 1] -= c;
    }
    
    for (int i = 1; i <= n; i ++ ) a[i] = b[i] + a[i - 1];

	for (int i = 1; i <= n; i ++ ) cout << a[i] << ' ';
    
	return 0; 
}

3.2 二维差分

bij是空想处理的，满足aij是b数组的前缀和，给定a数组，假想一个b数组。使得a数组是b数组的前缀和，而b数组则是a数组前缀和的逆运算。

代码:

#include 

using namespace std;

const int N = 1010;

int a[N][N], b[N][N];
int n, m, q;

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main()
{
    cin >> n >> m >> q;
    
    //读入数据
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ ) 
            cin >> a[i][j];
    
    //进行构造
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            insert(i, j, i, j, a[i][j]);
    
    //做q个询问
    while ( q -- )
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }
    
    //求a数组
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];
    
    for (int i = 1; i <= n; i ++ )
    {
       for (int j = 1; j <= m; j ++ )
       {
            cout << a[i][j] << ' ';
       }
       puts("");
    }
    return 0;
}

四、习题汇总

类型	题目
二分	AcWing 789. 数的范围
	AcWing 790. 数的三次方根
高精度	AcWing 791. 高精度加法
	AcWing 792. 高精度减法
	AcWing 793. 高精度乘法
	AcWing 794. 高精度除法
前缀和与差分	AcWing 795. 前缀和
	AcWing 796. 子矩阵的和
	AcWing 797. 差分
	AcWing 798. 差分矩阵