【笔记】AOV网与拓扑排序

1.无环路有向图

  不存在有向环路的有向图称为无环路有向图（简写为dag）。一个无环路有向图对应的无向图可能存在环路，但它不存在有向环路。除非特别声明，有向图中的环路均指有向环路。
  无环路有向图可用于表示偏序集。

2.AOV网

  在每一个工程中，可以将工程分为若干个子工程，这些子工程称为活动。如果用图中的顶点表示活动，以有向图的弧表示活动之间的优先关系，这样的有向图称为AOV网，即顶点表示活动的网。在AOV网中，如果从顶点 vi 到顶点 vj 之间存在一条路径，则顶点 vi 是顶点 vj 的直接前驱，顶点 vj 是顶点 vi 的直接后继。活动中的制约关系可以通过AOV网中的表示。
  在AOV网中，不允许出现环，如果出现环就表示某个活动是自己的先决条件。因此需要对AOV网判断是否存在环，可以利用有向图的拓扑排序进行判断。

3.拓扑排序

  拓扑排序就是将AOV网中的所有顶点排列成一个线性序列，并且序列满足以下条件：在AOV网中，如果从顶点 vi 到 vj 存在一条路径，则在该线性序列中，顶点 vi 一定出现在顶点 vj 之前。因此拓扑排序的过程就是将AOV网中的各个活动组成一个可行的实施方案。

  对AOV网进行拓扑排序的算法：
  1. 在AOV网中任意选择一个没有前驱的顶点，即顶点入度为零，将该顶点输出。
  2. 从AOV网中删除该顶点，并删除从该顶点出发的弧。
  3. 重复执行步骤1和步骤2，直达AOV网中所有都已经被输出，或者AOV网中不存在无前驱的顶点为止。

  按照上述步骤，AOV网的拓扑序列为 (C1,C2,C3,C4,C5,C6,C7,C8,C9,C10) 或 (C6,C7,C8,C9,C1,C2,C3,C4,C5,C10) 。
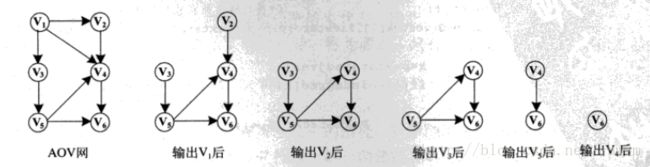
  下图是AOV网的拓扑序列的构造过程，其拓扑序列为 V1,V2,V3,V5,V4,V6 。

  在对AOV网进行拓扑排序结束后，可能会出现两种情况：一种是AOV网中的顶点全部输出，表示网中不存在回路；另一种是AOV网中还存在没有输出的顶点，剩余的未输出顶点的入度都不为零，表示网中存在回路。

4.AOV网的拓扑排序算法实现

  采用邻接表存储的AOV网的拓扑排序的算法实现：遍历邻接表，将各个顶点入度保存在数组indegree中。将入度为零的顶点入栈，依次将栈顶元素出栈并输出该顶点，对该顶点的邻接顶点的入度减1，如果邻接顶点的入度为零，则入栈；否则，将下一个邻接顶点的入度减1并进行相同的处理。然后继续将栈中元素出栈，重复执行以上过程，直到栈空为止。

int TopologicalSort(AdjGraph N)
/*有向图G的拓扑排序。如果图G没有回路，则输出G的一个拓扑序列并返回1，否则返回0*/
{
    int i,k,count=0;
    int indegree[MaxSize];      /*数组indegree存储各顶点的入度*/
    SeqStack S;
    ArcNode *p;
    /*将图中各顶点的入度保存在数组indegree中*/
    for(i=0;i/*将数组indegree赋初值*/
        indegree[i]=0;
    for(i=0;iwhile(p!=NULL)
        {
            k=p->adjvex;
            indegree[k]++;
            p=p->nextarc;
        }
    }
    InitStack(&S);              /*初始化栈S*/
    printf("拓扑序列：");
    for(i=0;iif(!indegree[i])        /*将入度为零的顶点入栈*/
            PushStack(&S,i);
        while(!StackEmpty(S))   /*如果栈S不为空*/
        {
            PopStack(&S,&i);    /*从栈S将顶点j弹出，输出该顶点*/
            printf("%s ",N.vertex[i].data);
            count++;            /*对入栈T的顶点计数*/
            for(p=N.vertex[i].firstarc;p;p=p->nextarc)  /*处理编号为i的顶点的每个邻接点*/
            {
                k=p->adjvex;            /*顶点序号为k*/
                if(--indegree[k]==0)    /*如果k的入度减1后变为0，则将k入栈S*/
                    PushStack(&S,k);
            }
        }
        if(count"该有向网有回路\n");
            return 0;
        }
        else
            return 1;
}

  对有n个顶点和e条弧的有向图来说，建立求各顶点的入度的时间复杂度为 O(e) ，将零入度的顶点入栈的时间复杂度为 O(n) ；在拓扑排序过程中，若有向图无环，则每个顶点进一次栈，出一次栈，入度减1操作在while语句中总共执行e次，因此拓扑排序总的时间复杂度为 O(n+e) 。