ShengBTE简单介绍、安装与使用

ShengBTE用迭代法求解声子的完全线性化玻尔兹曼输运方程。这远远超出了广泛使用的弛豫时间近似(relaxation-time  approximation)；在“正常”(准动量守恒)三声子过程起相关作用的材料中，这种差异可能很重要。

通过使用来自从头计算的输入，ShengBTE产生具有预测能力的结果，而不需要拟合实验。

目前可以研究两种体系:块状晶体材料及其纳米线。前者主要的声子散射机制是三声子过程和同位素无序。而这些都可以在ShengBTE实现:

同位素散射:使用田村公式（Tamura's formula）实现。公式中出现的状态的投影振动密度是用局部自适应展宽算法计算的。

三声子过程:从能量的一组三阶导数计算出三声子散射振幅。关键的一点是加强能量守恒，以便只考虑允许的过程。与解决问题的其他方法相反，在ShengBTE中，这个问题是使用局部自适应的无参数方法来解决的。

作为输入，ShengBTE需要一组二阶和三阶原子间力常数，可能还需要固体的介电参数值。

这组变量通常是计算出来的从头算DFT软件包，例如VASP或者Quantum Espresso。在某些情况下，这些程序可以直接计算二阶常数；在其他情况下，需要Phonopy等辅助软件来促进这个过程。而ShengBTE的作者同时开发了软件thirdorder，在三阶计算中扮演类似的角色。

除了热导率张量，ShengBTE还输出以下量:

• 取样q点的声子频率。

• 声子群速度。

• 晶格比热。

• 单位平均自由程的纳米颗粒热导率。

• 能量守恒允许处理的三声子部分，有时称为三声子相空间。

• 模式对三声子相空间的贡献。

• 态的振动密度:总量和投影。

• 每模式对热导率的贡献。

• 累积热导率:平均自由程小于阈值的声子对此量的贡献。

• 散射率:总量、区域贸易协定值、同位素和非谐波贡献。

• 沿块体任意晶向切割的纳米线的热导率。

• 总计和模式Grüneisen参数。

精确描述三声子散射所需的能量的三阶导数的数量很容易达到几十万。因此，使用真实空间超级细胞方法进行的直接计算会消耗大量计算资源。通过利用系统的对称性，thirdorder.py通常可以将问题减少到几百次DFT运行。这意味着三阶计算仍将是该过程中计算成本最高的部分，但对于单一化合物甚至中等大小的库来说，这已经是可以接受的计算量了。

在安装前要检测软件安装所需安装环境，这里我采用自己在虚拟机上搭建的CentOS7系统，在root账户下安装好了Intel_parallel_studio和Anaconda3，并在此基础上准备安装ShengBTE和thirdorder所需要的基本库spglib。

安装环境：

• VMware Workstation Pro -16.0.0-16894299

• CentOS Linux release 7.9.2009 (Core)

• Linux version 3.10.0-957.el7.x86_64 

• gcc version ：10.2.0

• icc ifort icpc mpiifort : Intel_parallel_studio_xe_2019

• python3：Anaconda3-2021.11-Linux-x86_64

安装软件

spglib-1.9.7                        spglib download | SourceForge.net

ShengBTE-1.1.1                sousaw / ShengBTE / Downloads — Bitbucket

thirdorder-1.1.1                sousaw / thirdorder / Downloads — Bitbucket

Spglib安装

首先解压下载的spglib安装包，并在解压后的目录中新建一个build目录用做spglib的安装目录。

随后执行主目录的configure文件，生成Makefile文件，然后对spglib进行编译安装。

tar vzxf spglib-1.9.7.tar.gz
cd spglib-1.9.7/
mkdir build && cd build && pwd && cd ../
#建立安装文件夹，并输出安装目录路径
./configure –prefix=/opt/ShengBTE/spglib-1.9.7/build
#在安装目录中生成Makefile文件，并make编译
#注：/opt/ShengBTE/spglib-1.9.7/build是我此次安装时的目录，大家在具体安装时请适当调整。
make && make install

如果没有报错的话，spglib就编译完成了，spgib的安装主要是给ShengBTE准备一个libsymspg.a文件，当然在thirdorder安装的时候还需要别的文件，这些都可以在build目录里找到，具体路径要牢记，我们在后面的安装中会经常用到。

ShengBTE安装

由于最新下载的ShengBTE安装包是zip格式的压缩包，则不再需要tar命令解压，直接手动解压后拷贝到安装目录即可，在安装前需要先准备一个arch.make文件，而ShengBTE自带一个arch.make.examp文件，可以在此基础上修改并另存成arch.make文件再移动到Src文件夹下。

在arch.make.example的基础上，在前面编辑好libsymspg.a文件的路径，由于当前系统里安装的编译器为Intel_parallel_studio_xe_2019的mpiifort，所以在文件中也需要将mpif90改为mpiifort。

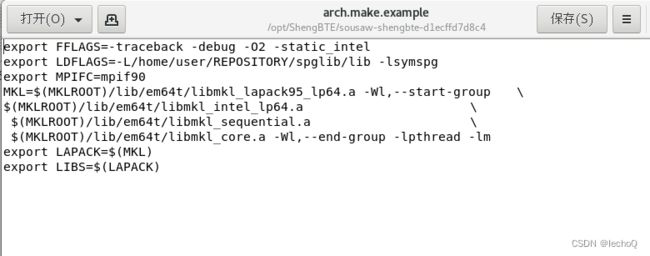
未修改的arch.make.example文件：

 修改后另存为arch.make文件：

export FFLAGS=-traceback -debug -O2 -static_intel
export LDFLAGS=/opt/ShengBTE/spglib-1.9.7/build/lib/libsymspg.a 
#注：这里的/opt/ShengBTE/spglib-1.9.7/build是我自己安装时的文件夹，具体安装的时候请调整。
export MPIFC=mpiifort
#注：我所使用的编译器为Intel_parallel_studio_xe_2019的mpiifort，具体安装的时候如果报错不能识别mpiifort请根据安装环境适当调整
MKL=$(MKLROOT)/lib/intel64/libmkl_lapack95_lp64.a -Wl,--start-group \
$(MKLROOT)/lib/intel64/libmkl_intel_lp64.a           \
$(MKLROOT)/lib/intel64/libmkl_sequential.a           \
$(MKLROOT)/lib/intel64/libmkl_core.a -Wl,--end-group -lpthread -lm
export LAPACK=$(MKL)
export LIBS=$(LAPACK)

这里主要是补充了我们make编译出的libsymspg.a文件的路径，以及更改了编译器为mpiifort，在下方也调整了MKL的配置，大家在安装的时候可以复制上方的内容，手动更改libsymspg.a文件的路径，然后可以尝试进行安装。

接下来直接在Src文件夹内执行命令make就可以了

等待编译完成后会在上级目录中生成ShengBTE的执行文件。

这里进入Test-QE文件夹，按照软件自带的测试文件对已安装的ShengBTE软件进行测试。

cd Test-QE
#which mpirun
mpirun -np 2 ../ShengBTE

这里我检查了一下mpirun的位置，是因为虚拟机里有着Intel_parallel_studio_xe_2019和openMPI等多版本的mpirun，大家自行测试的时候可以跳过这一段。

 可以看到ShengBTE已经可以正常运行，并输出计算结果。

之后我们便可以手动修改环境变量，将编译好的ShengBTE执行文件添加到环境变量中，在~/.bashrc文件最后添加如下一行,其中$ShengBTE是代表的你安装ShengBTE的文件路径也就是ShengBTE执行文件所在的目录

export PATH=/opt/ShengBTE/ShengBTE:$PATH
#注:/opt/ShengBTE/ShengBTE是我此次安装ShengBTE的路径，具体安装时请适当调整

这样就可以在提交任务运行ShengBTE的时候不用再去找执行文件的路径或者把它拷贝到你计算的文件夹里去啦。当你需要执行计算的时候只需要输入下面的命令就可以了，其中N代表你所使用的核数。

mpirun -np N ShengBTE |tee  BTE.out

Thirdorder安装

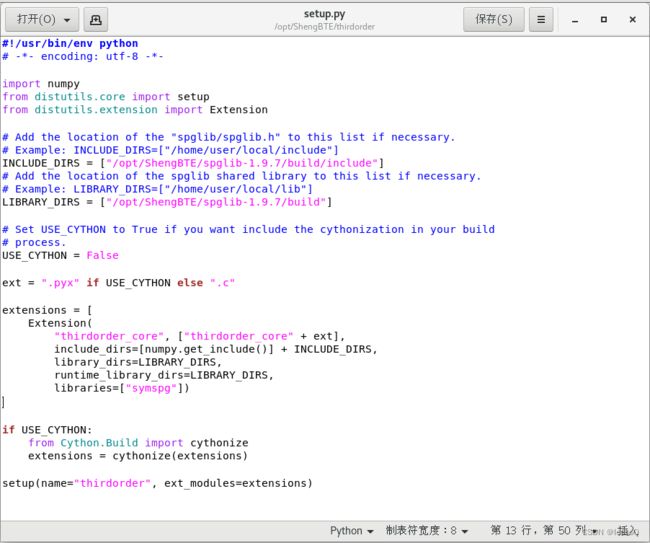
我们将解压后的thirdorder文件夹拷贝到安装目录，进入目录首并检查setup.py文件

在文件中间提示我们要添加spglib.h文件和spglib的shared library 文件夹路径到这个setup.py文件中，这时我们便根据之前已经安装好的spglib的安装路径补充进去。

其中spglib.h文件在/opt/ShengBTE/spglib-1.9.7/build/include/spglib文件夹内，而shared library文件夹则为上层目录中的lib文件夹，路径为/opt/ShengBTE/spglib-1.9.7/build/lib，完善后的setup.py文件如下。

保存后我们在安装文件夹中执行命令运行 compile.sh进行安装

sh compile.sh

如果在安装过程中出现例如gcc报错或lapacke.h或python.h等问题，需要适安装环境处理。这次安装前已经安装好了Anaconda3包并配置好环境变量，安装过程相对简单，具体安装请参加其他教程。

安装完成后文件夹内会出现文件thirdorder_core.cpython-38-x86_64-linux-gnu.so，这个有和其他安装教程做对比，可能会有一定不同，但接下来对所安装的thirdorder进行测试即可证明安装是否成功。

首先我们配置一下thirdorder的环境变量，与ShengBTE类似

export PATH=/opt/ShengBTE/thirdorder:$PATH
#注:/opt/ShengBTE/thirdorder是我此次安装thirdorder的路径，具体安装时请适当调整

我们找一个测试文件夹，在文件夹中准备好一个VASP计算所需要的POSCAR文件，例如一个含有两个Si原子的晶胞

cubic diamond
   5.5
 0.0    0.5     0.5
 0.5    0.0     0.5
 0.5    0.5     0.0
 Si
  2
Direct
 -0.125 -0.125 -0.125
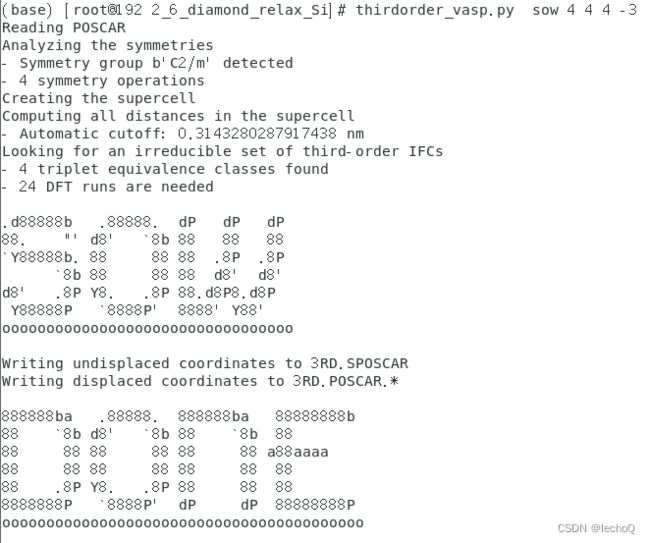
  0.125  0.125  0.130 

然后我们在文件夹中执行如下命令然后我们在文件夹中执行如下命令

thirdorder_vasp.py sow 4 4 4 -3

得到输出界面如下

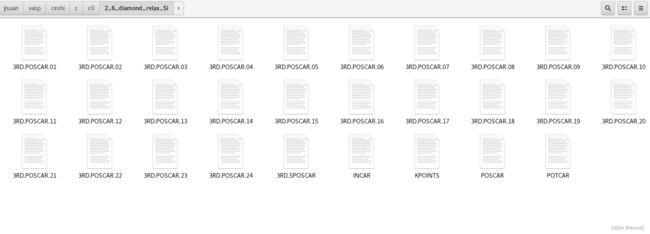
 在测试文件夹内同时也得到了24个3RD.POSCAR和一个SPOSCAR。代表我们thirdorder安装成功并可以直接运行。

ShengBTE和thirdorder的使用

在ShengBTE和thirdorder安装文件中均带有其“使用说明书”，且都命名为README.md，里面有一些基本的安装、使用介绍，尤其是一些参数的介绍，初学者在使用之前要认真阅读并理解，对以后遇到问题有很大帮助，这也是对于软件的最基础的了解。

鉴于笔者能力有限，在此不对说明文件做解读，大家可以在以下网址下载到ShengBTE和thirdorder的说明文件，我也会附加在文末供大家阅读。

https://www.shengbte.org/documentationhttps://bitbucket.org/sousaw/shengbte/src/master/https://bitbucket.org/sousaw/thirdorder/src/master/

另外在此也向大家推荐天玑算王宁老师的关于phonopy、thirdorder与ShengBTE的教学视频。

天玑算

这里有你最关心的科研资讯、每周精选文献、免费计算类课程、顶刊解读和学术干货。还能与优秀硕博、科研大佬、同行学者们相互交流，一起学习，共同成长！

https://www.bilibili.com/video/BV1wo4y1U772/?spm_id_from=333.788.videocard.1https://www.bilibili.com/video/BV1rL41147Rg?spm_id_from=333.999.0.0https://www.bilibili.com/video/BV1Yh411n7tx?spm_id_from=333.999.0.0

附注一：ShengBTE  README.md

# `ShengBTE`: a solver for the Boltzmann transport equation for phonons

## Authors:

- Wu Li 
- Jesús Carrete Montaña 
- Nebil A. Katcho 
- Natalio Mingo 

## How to download, compile and use `ShengBTE`

Development of `ShengBTE` is hosted at [Bitbucket](https://www.bitbucket.org/). The latest version can be downloaded using the "download" link at [https://bitbucket.org/sousaw/shengbte](https://bitbucket.org/sousaw/shengbte). Alternatively, it is possible to clone its [GIT](http://git-scm.com/) repository from the command line with

```bash
git clone [email protected]/sousaw/shengbte.git ShengBTE
```

or from one of the many graphical frontends available.

To compile the code it is enough to run `make` in the `Src` subdirectory of the distribution, but a suitable `arch.make` must be present in that directory. An example is provided as `arch.make.example`. As a minimum, `$MPIFC` must contain a valid command to compile Fortran 90 code with MPI directives, while the combination of `$LDFLAGS` and `$LIBS` must contain any linker flags required in order to link against an implementation of `LAPACK` and against Atsushi Togo's [spglib](http://spglib.sourceforge.net/). ShengBTE uses some Fortran 2003 extensions, most notably its new syntax for array initialization, and a recent Fortran compiler is required that supports them; `gfortran` 4.8.2 and `ifort` 12.0.0 are known to work.

After compilation succeeds, a `ShengBTE` binary will be created in the root directory of the distribution. This executable takes no command-line options and accepts no input from the terminal. It can be invoked simply as

```bash
./ShengBTE
```

for serial mode, but most often it will be run using a command like

```bash
mpirun -n 32 ./ShengBTE 2>BTE.err >BTE.out
```

often as part of a script to be submitted to a batch system.

## Input files

Exactly three files are required for a `ShengBTE` run: `CONTROL`, one of `FORCE_CONSTANTS_2ND` or `espresso.ifc2`, and `FORCE_CONSTANTS_3RD`. Their contents are detailed below; for a complete example, the reader is referred to the `Test-VASP` and `Test-QE` subdirectories of the distribution.

### The `CONTROL` file

The contents of this file describe the system to be studied and specify a set of parameters and flags controlling execution. Its format is merely a sequence of four Fortran [namelists](http://publib.boulder.ibm.com/infocenter/lnxpcomp/v8v101/index.jsp?topic=%2Fcom.ibm.xlf101l.doc%2Fxlflr%2Fnamelistio.htm), with a reasonably flexible syntax that should become apparent after looking at the example `Test-*/CONTROL` for zincblence InAs and GaAs. Some parameters and flags are mandatory, whereas others are optional and take a default value when unspecified.

- `&allocations` namelist:
    - `nelements` (integer, mandatory): number of different elements in the compound
    - `natoms` (integer, mandatory): number of atoms in the unit cell
    - `ngrid` (integer, 3, mandatory): number of grid planes along each axis in reciprocal space
    - `norientations` (integer, default=0): number of orientations along which to study nanowires
- `&crystal` namelist:
    - `lfactor` (real, nm, default=1.0): unit of measurement for lattice vectors
    - `lattvec` (real, 3 x 3, mandatory): real-space lattice vectors, in units of `lfactor`
    - `types` (integer, `natoms`, mandatory): a vector of `natom` integers, ranging from 1 to `nelements`, assigning an element to each atom in the system
    - `elements` (string, `nelements`, mandatory): a vector of element names
    - `positions` (real, 3 x `natoms`, mandatory): atomic positions in lattice coordinates
    - `masses` (real, `nelements`, g/mol, default=automatic): atomic masses corresponding to each element. If they are omitted and `autoisotopes` is true and the element names are known, they are computed automatically.
    - `gfactors` (real, `nelements`, default=automatic): g factors for isotopic scattering associated to each element. If they are omitted and `autoisotopes` is true and the element names are known, they are computed automatically.
    - `epsilon` (real, 3 x 3, Ε0, default=1): dielectric tensor of the system in the Cartesian basis
    - `born` (real, 3 x 3 x `natoms`, e, default=0): Born effective charge tensor of each atom in the Cartesian basis
    - `scell` (integer, 3, mandatory): supercell sizes along each crystal axis used for the 2nd-order force constant calculation
    - `orientations` (integer, 3 x `norientations`, mandatory unless `norientations`==0): terns of integer indices defining the crystallographic directions along which to study nanowires
- `¶meters` namelist:
    - `T` (real, K): temperature to be used in the case of single temperature calculation
    - `T_min`,`T_max`,`T_step` (real, K): the minimum temperature, the maximum temperature and the increment to be used for multiple-temperature calculation. T takes the priority if it is present. 
    - `omega_max` (real, rad/ps, default=1.e100): the max angular frequency up to which the anharmonic scattering properties are calculated for limited purposes. 
    - `scalebroad` (real, default=1.0): scale parameter for Gaussian smearing. The default is theoretically guaranteed to work, but significant speedups can sometimes be achieved by reducing it, with negligible loss of precision.
    - `rmin` (real, nm, default=5.0): minimum radius of nanowires whose thermal conductivity will be computed
    - `rmax` (real, nm, default=505.0): maximum radius of nanowires whose thermal conductivity will be computed
    - `dr` (real, nm, default=100.0): radius increment to be used when simulating nanowires from `rmin` to `rmax`
    - `maxiter` (integer, default=1000): maximum number of iterations allowed in the BTE convergence process
    - `nticks` (integer, default=100): number of different values of the mean free path at which to compute the cumulative thermal conductivity
    - `eps` (real, default=10-5): the iterative solver of the BTE will stop when the relative change in the thermal conductivity tensor is less than `eps`. Such change between steps n-1 and n is measured as ||Κn-Κn-1||, where ||⋅||  denotes a matrix 2-norm.
- `&flags` namelist:
    - `nonanalytic` (logical, default=.true.): compute and use the nonanalytic part of the dynamical matrix
    - `convergence` (logical, default=.true.): if true, iterate the BTE solver until convergence is achieved. If false, compute thermal conductivities in the relaxation time approximation.
    - `isotopes` (logical, default=.true.): include isotopic scattering in the relaxation times
    - `autoisotopes` (logical, default=.true.): compute atomic masses and g factors automatically
    - `nanowires` (logical, default=.false.): study the thermal conductivity of nanowires in addition to that of the bulk
    - `onlyharmonic` (logical, default=.false.): stop the program after computing the specific heat and small-grain thermal conductivity
    - `espresso` (logical, default=.false.): read second-order force constants from `espresso.ifc2` (Quantum Espresso format) instead of the default `FORCE_CONSTANTS_2ND` (Phonopy format)

### The `FORCE_CONSTANTS_2ND` file

This file contains the second derivatives of the system's energy with respect to the Cartesian coordinates of the nuclei, _i.e._ the interatomic force constant matrix. Its format is precisely that chosen in [Phonopy](http://phonopy.sourceforge.net/) for the `FORCE_CONSTANTS` file, so that the result of a Phonopy calculation can be used directly. The first line of the file declares the total number of atoms in the supercell, `npairs`, which must be equal to `scell(1)` x `scell(2)` x `scell(3)` x `natoms`, and is followed by `npairs` blocks of four lines each. The first line of each of those blocks contains two integers with the 1-based indices of the atoms forming the pair; the remaining three lines contain the 3 x 3 matrix of second-order interatomic force constants linking those two atoms, in eV/Å2.

### The `espresso.ifc2` file

The information contained in this file is equivalent to that in `FORCE_CONSTANTS_2ND`, but the format is different. For details, consult the [Quantum ESPRESSO](http://www.quantum-espresso.org/) documentation. Please note that although this file's header contains information about lattice vectors, atomic positions, Born effective charges and so forth, it is ignored by `ShengBTE`. It is the user's responsibility to ensure that `espresso.ifc2` and `CONTROL` are compatible.

### The `FORCE_CONSTANTS_3RD` file

Similarly, this file contains the third-order interatomic force constant matrix, but uses a sparse description to save space. All constants are implicitily refered to a central unit cell i taken as the origin of coordinates. The first line again contains a single integer, `nb`, which is followed by `nb` blocks with the following structure:

- A blank line
- A 1-based sequential index
- A line with the Cartesian coordinates of the second unit cell in Å
- A line with the Cartesian coordinates of the third unit cell in Å
- A line with the 1-based indices of the three atoms involved, each from 1 to `natoms`
- 27 lines, each of which starts with a tern of integers specifying three Cartesian axes and is completed by a force constant in eV/Å3. The last element of the tern changes first.

The following is an example of one such block:

```
  
  1
  0.000  0.000  0.000
  0.000  0.000  0.000
  1 1 1
  1 1 1    0.0000000000E+00
  1 1 2    0.0000000000E+00
  1 1 3    0.0000000000E+00
  1 2 1    0.0000000000E+00
  1 2 2    0.0000000000E+00
  1 2 3    0.2346653425E+02
  1 3 1    0.0000000000E+00
  1 3 2    0.2346653425E+02
  1 3 3    0.0000000000E+00
  2 1 1    0.0000000000E+00
  2 1 2    0.0000000000E+00
  2 1 3    0.2346653425E+02
  2 2 1    0.0000000000E+00
  2 2 2    0.0000000000E+00
  2 2 3    0.0000000000E+00
  2 3 1    0.2346653425E+02
  2 3 2    0.0000000000E+00
  2 3 3    0.0000000000E+00
  3 1 1    0.0000000000E+00
  3 1 2    0.2346653425E+02
  3 1 3    0.0000000000E+00
  3 2 1    0.2346653425E+02
  3 2 2    0.0000000000E+00
  3 2 3    0.0000000000E+00
  3 3 1    0.0000000000E+00
  3 3 2    0.0000000000E+00
  3 3 3    0.0000000000E+00
```

## Output files

Many files including temperature-dependent directories are created during a successful run of `ShengBTE`. They contain not only the thermal conductivity and related quantities, but also a set of intermediate results that may be useful to diagnose problems. For some quantites, values only for the q points in the irreducible wedge are output, values for the rest can be recovered by looking into the equivilent points in the irreducible wedge.  This section includes a brief description of their contents.

- `BTE.ReciprocalLatticeVectors`: three reciprocal lattice basis vectors b1, b2 and b3 in nm-1. 
- `BTE.qpoints`: This file gives q points in the irreducible wedge of Brillouin zone (BZ), of which the relative coordinates with respect to the reciprocal lattice vectors are shown in the last 3 columns. The 1st and 2nd columns correspond the indices of those q points numbered in the irreducible wedge and in the whole Brillouin zone, respectively. The 3rd column lists the corresponding degeneracies. 
- `BTE.qpoints_full`: this file lists all q points in `ngrid(1)` x `ngrid(2)` x `ngrid(3)` Γ-centered regular grid. The 1st column is a sequentially increasing index, the 2nd column contains the index of the equivalent irreducible q point numbered in the irreducible wedge, and the 3 remaining columns are the relative coordinates with respect to the reciprocal lattice vectors for the q point.
- `BTE.omega`: phonon angular frequencies of those q points in the irreducible wedge, in rad/ps.
- `BTE.v`: group velocities of those modes (q index changes first, and then band index) in the irreducible wedge, in km/s (or nm THz)
- `BTE.v_full`: group velocities of all modes (q index changes first, and then band index)for all points listed in `BTE.qpoints_full`
- `BTE.w_boundary`: boundary scattering rate (in ps-1 , 2nd column) obtained for a characteristic length L=1 nm and a specularity parameter p=0 vs angular frequency (in rad/ps, 1st column) for those modes (q index changes first, and then band index) in the irreducible wedge.
- `BTE.w_isotopic`: isotopic scattering rate (in ps-1 , 2nd column) vs angular frequency (in rad/ps, 1st column) for those modes (q index changes first, and then band index) in the irreducible wedge.
- `BTE.dos`: the phonon density of states (2nd column) vs the angular frequencies (1st column, in rad/ps)
- `BTE.pdos`: the phonon density of states projected on each atom in the unit cell (from the 2nd column on) vs the angular frequencies (1st column, in rad/ps)
- `BTE.P3`: volume in phase space available for three-phonon processes, for each irreducible q point and phonon band
- `BTE.P3_total`: sum of all the contributions in `BTE.P3`, total volume in phase space available for three-phonon processes
- `BTE.P3_plus*`, `BTE.P3_minus*`: equivalents of `BTE.P3` and `BTE.P3_total`, but including only contributions from emission (minus) or absorption (plus) processes
- `BTE.gruneisen`: Grüneisen parameter for each irreducible q point and phonon band
- `BTE.cvVsT`: specific heat of the system, in J/\(m3 K) as a function of T (1st column)
- `BTE.gruneisenVsT_total`: total Grüneisen parameter obtained as a weighted sum of the mode contributions as a function of T (1st column)
- `BTE.KappaTensorVsT_sg`:  thermal conductivity tensor per unit of mean free path in the small-grain limit, in W/(m K nm) as a function of T (1st column). 
- `BTE.KappaTensorVsT_RTA`: total thermal conductivity tensor in unit of W/(m K) in the Relaxation Time Approximation (zero-order) as a function of T (1st column). 
- `BTE.KappaTensorVsT_CONV`: total CONVerged thermal conductivity tensor in unit of W/(m K) as a function of T (1st column). The last column gives the number of iterations reaching convergence.

Under temperature-dependent directories:

- `BTE.cv`: specific heat of the system, in J/\(m3 K)
- `BTE.kappa_sg`: thermal conductivity per unit of mean free path in the small-grain limit, in W/(m K nm)
- `BTE.gruneisen_total`: total Grüneisen parameter obtained as a weighted sum of the mode contributions
- `BTE.WP3`: weighted phase space available for three-phonon processes  (in ps4rad-4 , 2nd column) vs angular frequency (in rad/ps, 1st column) for those modes (q index changes first, and then band index) in the irreducible wedge. See [Phys. Rev. B 91, 144304 (2015)] for definition of weighted phase space.
- `BTE.WP3_plus`: WP3 contributed by phonon absorption processes alone
- `BTE.WP3_minus`: WP3 contributed by phonon emission processes alone
- `BTE.w_anharmonic`: contribution of three-phonon processes to the scattering rate, for each q point and each band, in ps-1
- `BTE.w`: total zeroth-order scattering rate for each q point and each band, in ps-1
- `BTE.w_final`: total converged scattering rate for each irreducible q point and each band, in ps-1
- `BTE.kappa`: tensorial contribution to the thermal conductivity from each band, in W/(m K). The last line contains converged values, the rest show the convergence process.
- `BTE.kappa_tensor`: total thermal conductivity, a 3 x 3 tensor expressed in W/(m K). The last line contains converged values, the rest show the convergence process.
- `BTE.kappa_scalar`: average of diagonal elements of the thermal conductivity tensor, in W/(m K). The last line contains converged values, the rest show the convergence process.
- `BTE.kappa_nw_*`: thermal conductivities of nanowires built along different directions of the bulk material, for different radii. The first column in each file is a diameter, the following 3 x `natoms` contain the contributions of each band and the last column contains the total thermal conductivity. Diameters are expressed in nm and conductivities in W/(m K)
- `BTE.kappa_nw_*_lower`: lower bounds to the thermal conductivities of nanowires built along different directions of the bulk material, for different radii. The first column in each file is a diameter, the following 3 x `natoms` contain the contributions of each band and the last column contains the total thermal conductivity. Diameters are expressed in nm and conductivities in W/(m K). Each lower bound is estimated by using the set of zeroth-order bulk relaxation times.
- `BTE.cumulative_kappa_*`: this set of files is analogous to `BTE.kappa*`, except in that their 1st column specifies a cutoff mean free path (in nm) when calculating the total contribution.
- `BTE.cumulative_kappaVsOmega_tensor`: this is analogous to `BTE.cumulative_kappa_tensor`, except in that the 1st column specifies a cutoff angular frequency (in rad/ps) when calculating the total contribution.

附注二：thirdorder README.md

# thirdorder #

The purpose of the thirdorder scripts is to help users of [ShengBTE](https://bitbucket.org/sousaw/shengbte) and [almaBTE](http://www.almabte.eu) create FORCE\_CONSTANTS\_3RD files in an efficient and convenient manner. More specifically, it performs two tasks:

1) It resolves an irreducible set of atomic displacements from which to compute the full anharmonic interatomic force constant (IFC) matrix. The displaced supercells are saved to input files that can be fed to first-principles DFT codes for calculating the forces arising from the atomic displacements. Currently supported DFT codes are VASP (thirdorder_vasp.py), Quantum ESPRESSO (thirdorder_espresso.py). and CASTEP (thirdorder_castep.py).

2) From the output files created by the DFT code, thirdorder reconstructs the full IFC matrix and writes it in the right format to FORCE\_CONSTANTS\_3RD.

# Compilation #

thirdorder is a set of Python scripts. It was developed using Python 2.7.3, but should work with slightly older versions. In addition to the modules in Python's standard library, the numpy and scipy numerical libraries are required. Moreover, this script relies on a module, thirdorder\_core, which is written in Cython. Thus, in spite of Python being an interpreted language, a compilation step is needed. Note that in addition to the .pyx source we also distribute the intermediate .c file, so Cython itself is not needed. The only requirements are a C compiler, the Python development package and Atsushi Togo's [spglib](http://spglib.sourceforge.net/).

Compiling can be as easy as running

```bash
./compile.sh
```

However, if you have installed spglib to a nonstandard directory, you will have to perform some simple editing on setup.py so that the compiler can find it. Please refer to the comments in that file.

# Usage #

After a successful compilation, the directory will contain the compiled module thirdorder\_core.so, thirdorder_common.py and DFT-code specific interfaces (e.g. thirdorder_vasp.py). All are needed to run thirdorder. You can either use them from that directory (maybe including it in your PATH for convenience) or copying the .py files to a directory in your PATH and thirdorder\_core.so to any location where Python can find it for importing.

# Running thirdorder with VASP #

Any invocation of thirdorder_vasp.py requires a POSCAR file with a description of the unit cell to be present in the current directory. The script uses no other configuration files, and takes exactly five mandatory command-line arguments:

```bash
thirdorder_vasp.py sow|reap na nb nc cutoff[nm/-integer]
```

The first argument must be either "sow" or "reap", and chooses the operation to be performed (displacement generation or IFC matrix reconstruction). The next three must be positive integers, and specify the dimensions of the supercell to be created. Finally, the "cutoff" parameter decides on a force cutoff distance. Interactions between atoms spaced further than this parameter are neglected. If cutoff is a positive real number, it is interpreted as a distance in nm; on the other hand, if it is a negative integer -n, the maximum distance among n-th neighbors in the supercell is automatically determined and the cutoff distance is set accordingly.

The following POSCAR describes the relaxed geometry of the primitive unit cell of InAs, a III-V semiconductor with a zincblende structure:

```
InAs
   6.00000000000000
     0.0000000000000000    0.5026468896190005    0.5026468896190005
     0.5026468896190005    0.0000000000000000    0.5026468896190005
     0.5026468896190005    0.5026468896190005    0.0000000000000000
   In   As
   1   1
Direct
  0.0000000000000000  0.0000000000000000  0.0000000000000000
  0.2500000000000000  0.2500000000000000  0.2500000000000000
```

Let us assume that such POSCAR is in the current directory and that thirdorder_vasp.py is in our PATH. To generate an irreducible set of displacements for a 4x4x4 supercell and up-to-third-neighbor interactions, we run

```bash
thirdorder_vasp.py sow 4 4 4 -3
```

This creates a file called 3RD.SPOSCAR with the undisplaced supercell coordinates and 144 files with names following the pattern 3RD.POSCAR.*. It is the latter that need to be input to VASP. This step is completely system-dependent, but suppose that in ~/vaspinputs we have the required INCAR, POTCAR and KPOINTS files as well as a runvasp.sh script that can be passed to qsub. We can run a command sequence like:

```bash
for i in 3RD.POSCAR.*;do
   s=$(echo $i|cut -d"." -f3) &&
   d=job-$s &&
   mkdir $d &&
   cp $i $d/POSCAR &&
   cp ~/vaspinputs/INCAR ~/vaspinputs/POTCAR ~/vaspinputs/KPOINTS $d &&
   cp ~/vaspinputs/runvasp.sh $d &&
   (cd $d && qsub runvasp.sh)
done
```

Some time later, after all these jobs have finished successfully, we only need to feed all the vasprun.xml files in the right order to thirdorder_vasp.py, this time in reap mode:

```bash
find job* -name vasprun.xml|sort -n|thirdorder_vasp.py reap 4 4 4 -3
```

If everything goes according to plan, a FORCE\_CONSTANTS\_3RD file will be created at the end of this run. Naturally, it is important to choose the same parameters for the sow and reap steps.

# Running thirdorder with Quantum ESPRESSO #

The invocation of thirdorder_espresso.py requires two files:

1) an input file of the unit cell with converged structural parameters

2) a template input file for the supercell calculations. The template file is a normal QE input file with some wildcards

The following input file GaAs.in describes the relaxed geometry of the primitive unit cell of GaAs, a III-V semiconductor with a zincblende structure

```
&CONTROL
 calculation='scf',
 prefix='gaas',
 restart_mode='from_scratch',
 tstress = .true.,
 tprnfor = .true.,
/
&SYSTEM
 ibrav=0,
 nat=2,
 ntyp=2,
 ecutwfc=48
 ecutrho=384
/
&ELECTRONS
 conv_thr=1.d-12,
/
ATOMIC_SPECIES
 Ga  69.723    Ga.pbe-dnl-kjpaw_psl.1.0.0.UPF
 As  74.92160  As.pbe-dn-kjpaw_psl.1.0.0.UPF
ATOMIC_POSITIONS crystal
 Ga 0.00 0.00 0.00
 As 0.25 0.25 0.25
K_POINTS automatic
11 11 11 0 0 0
CELL_PARAMETERS angstrom
   0.000000000   2.857507756   2.857507756
   2.857507756   0.000000000   2.857507756
   2.857507756   2.857507756   0.000000000
```

thirdorder_espresso.py supports the following QE input conventions for structural parameters:

1) ibrav = 0 together with CELL_PARAMETERS (alat | bohr | angstrom)

2) ibrav != 0 together with celldm(1)-celldm(6)

For ATOMIC_POSITIONS, all QE units are supported (alat | bohr | angstrom | crystal). Simple algebraic expressions for the positions are supported in similar fashion to QE. Please note that ibrav = 11..14  have not been tested so far with thirdorder_espresso.py (please report if you run these cases successfully or run into problems). Cases ibrav = -5, -9, -12, -13, and 91 are not currently implemented (but those structures can be defined via ibrav = 0 instead)

The following supercell template GaAs_sc.in is used for creating the supercell input files (note the ##WILDCARDS##):

```
&CONTROL
  calculation='scf',
  prefix='gaas',
  tstress = .true.,
  tprnfor = .true.,
  outdir = 'tmp_##NUMBER##'
/
&SYSTEM
  ibrav=0,
  nat=##NATOMS##,
  ntyp=2,
  ecutwfc=48
  ecutrho=384
/
&ELECTRONS
  conv_thr=1.d-12,
/
ATOMIC_SPECIES
 As  74.92160  As.pbe-dn-kjpaw_psl.1.0.0.UPF
 Ga  69.723    Ga.pbe-dnl-kjpaw_psl.1.0.0.UPF
##COORDINATES##
K_POINTS gamma
##CELL##
```

Please note that if Gamma-point k-sampling is used for the supercells, it is computationally much more efficient to apply "K_POINTS gamma" instead of "K_POINTS automatic" with the mesh set to "1 1 1 0 0 0". SCF convergence criterion conv_thr should be set to a tight value and parameters tstress and tprnfor are required so that thirdorder can extract the forces from the output file.

Thirdorder uses no other configuration files, and requires seven mandatory command-line arguments to create the supercell inputs with the "sow" operation:

```bash
thirdorder_espresso.py unitcell.in sow na nb nc cutoff[nm/-integer] supercell_template.in
```

Please see the above description for VASP for the explanation of the parameters na, nb, nc, and cutoff. For the present GaAs example, we execute:

```bash
thirdorder_espresso.py GaAs.in sow 4 4 4 -3 GaAs_sc.in
```

The command creates a file called BASE.GaAs_sc.in with the undisplaced supercell coordinates and 144 files with names following the pattern DISP.GaAs_sc.in.NNN The DISP files should be executed with QE. This step is completely system-dependent, but some practical suggestions can be extracted from the VASP example above.

After all the jobs have finished successfully, we only need to feed all the output files in the right order to thirdorder_espresso.py, this time in reap mode (now using only six arguments, the supercell argument is not used here):

```bash
find . -name 'DISP.GaAs_sc.in*out' | sort -n | thirdorder_espresso.py GaAs.in reap 4 4 4 -3
```

If everything goes according to plan, a FORCE_CONSTANTS_3RD file will be created at the end of this run. Naturally, it is important to choose the same parameters for the sow and reap steps.

# Running thirdorder with CASTEP #

Any invocation of thirdorder_castep.py requires a CELL and PARAM file with a description of the unit cell and parameters to be present in the current directory. The script uses no other configuration files, and takes 
exactly six mandatory command-line arguments:

```bash
thirdorder_castep.py sow|reap na nb nc cutoff[nm/-integer] 
```

The first argument must be either "sow" or "reap", and chooses the operation to be performed (displacement generation or irreducible force constant (IFC) matrix reconstruction). The next three must be positive integers, 
and specify the dimensions of the supercell to be created. The "cutoff" parameter specifies the force cutoff distance in nanometres; interactions between atoms further apart than this parameter are neglected. If cutoff is 
a negative integer -n, the cutoff is set automatically to the maximum distance of the n-th nearest neighbours in the supercell, e.g. if it is set to -3, the 3rd nearest-neighbour distances will be computed, and the cutoff set to the
 largest value. Finally,  is the file prefix for CASTEP's input/output files.

The following CELL file describes the relaxed geometry of the primitive unit cell of InAs, a III-V semiconductor with a zincblende structure:

```
%BLOCK LATTICE_CART
     0.000000000000000    3.015881337714003    3.015881337714003
     3.015881337714003    0.000000000000000    3.015881337714003
     3.015881337714003    3.015881337714003    3.015881337714003
%ENDBLOCK LATTICE_CART

%BLOCK POSITIONS_FRAC
In  0.0000000000000000  0.0000000000000000  0.0000000000000000
As  0.2500000000000000  0.2500000000000000  0.2500000000000000
%ENDBLOCK POSITIONS_FRAC

symmetry_generate
kpoints_mp_grid 5 5 5
```

Let us assume that such a CELL file is in the current directory along with an appropriate PARAM file, and that thirdorder_castep.py is in our PATH. To generate an irreducible set of displacements for a 4x4x4 supercell and 
up to third-nearest-neighbour interactions, we run:

```bash
thirdorder_castep.py sow 4 4 4 -3 InAs
```

This creates an InAs-3RD directory (``-3RD in the general case) with the undisplaced supercell coordinates and 144 subdirectories with names following the pattern job-*, which contain supercells with small perturbations 
to the atomic positions. Each job is a separate calculation which needs to be input to CASTEP. This step is completely system-dependent. As an example, on a given system the user could run the jobs in series with a command sequence like:

```bash
for i in {000..144}
do
 cd InAs-3RD/job-$i
 aprun -n ${n} castep.mpi InAs
 cd -
 echo "job-$i done" >> jobs_done.txt
done
```

It is necessary to complete all jobs in ``-3RD directory before proceeding to the REAP step. After the jobs have completed successfully, the output files have to be collated and passed to thirdorder_castep.py, this 
time in REAP mode. The general syntax is:

```bash
find -3RD/job* -name .castep | sort -n| thirdorder_castep.py reap nx ny nz cutoff seedname
```

For the InAs example, this would be:

```bash
find InAs-3RD/job* -name InAs.castep | sort -n| thirdorder_castep.py reap 4 4 4 -3 InAs
```

If everything goes well, a FORCE\_CONSTANTS\_3RD file will be created at the end of this run. Naturally, it is important to choose the same parameters (nx, ny, nz, cutoff) for the sow and reap steps. Use this 
FORCE\_CONSTANTS\_3RD file along with FORCE\_CONSTANTS\_2ND and CONTROL to perform a ShengBTE run. The [CASTEP2ShengBTE script](https://github.com/ganphys/castep2shengbte) can be useful for generating FORCE\_CONSTANTS\_2ND and CONTROL files from CASTEP calculations.

### Limitations of the CASTEP interface: 
- Spin-polarised calculations are not supported at the moment. Spin values will not be included in the supercell files.
- The initial .cell file MUST be in the following format:
    Lattice parameter, Cell contents AND THEN everything else.
- Only fractional coordinates are supported. Use only fractional coordinates.

### Hints and tips for CASTEP calculations:

- Use `write_checkpoint: none` in the ``.param file. Otherwise, the process of writing hundreds of checkpoint files to the hard drive will slow down the calculation process.
 
- It is possible to reuse a single checkpoint file for each of the runs. This should save you a couple of hours. For that purpose, generate a checkpoint file from one of the runs and place the file in the root directory where your input files are placed. Then add `reuse : ../../seedname.check` to your ``.param file in the root directory and either run once again thirdorder_castep.py in SOW mode paste the edited ``.param file to all subdirectories or copy and paste it manually.

- If you don't want to generate the pseudopotentials at the start of each run, you can add the following block to the end of the .cell in the root directory:

```
%BLOCK SPECIES_POT
In ../../In_C17_PBE_OTF.usp
As ../../As_C17_PBE_OTF.usp
%ENDBLOCK SPECIES_POT
```

愿有所成

IEchoQ

引喻失义   妄自菲薄

I