python numpy库教程_python教程1:numpy库

ps这篇文章是匆忙之下写的，上学了，日后更新，如果觉得这篇文章不好，请在评论区提出建议

咳咳，这里是没有语法讲解的，如果基础语法don't know可以点这里

ok，切入正题开始学习numpy库的使用，嗯，先放上看起来很官方的链接https://www.numpy.org.cn/

安装numpy什么的我就不说了

那么numpy是干什么的？

其实就是拿个n维数组玩来个玩

ok，那么它能玩出什么花样呢，先别急，来学习一下语法基础

依然是亲爱的termux

numpy数组

这是创建一个的一维数组，简单吧

其实如下写法也是可以的(注意，这里给numpy指定别名np)

变量名 = np.array([x,x,x,x,x])

变量名 = np.array((x,x,x,x,x))

变量名 = np.arange(x,x)

变量名 = np.linespace(x,x,x)

实例代码↓

a = np.array([0, 1, 2, 3, 4])

b = np.array((0, 1, 2, 3, 4))

c = np.arange(5)

d = np.linspace(0, 2*np.pi, 5)

这里np.pi即是圆周率前15位

运行结果↓

>>> a = np.array([0, 1, 2, 3, 4])

>>> b = np.array((0, 1, 2, 3, 4))

>>> c = np.arange(5)

>>> d = np.linspace(0, 2*np.pi, 5)

>>> print (a,b,c,d)

[0 1 2 3 4] [0 1 2 3 4] [0 1 2 3 4] [0. 1.57079633 3.14159265 4.71238898 6.28318531]

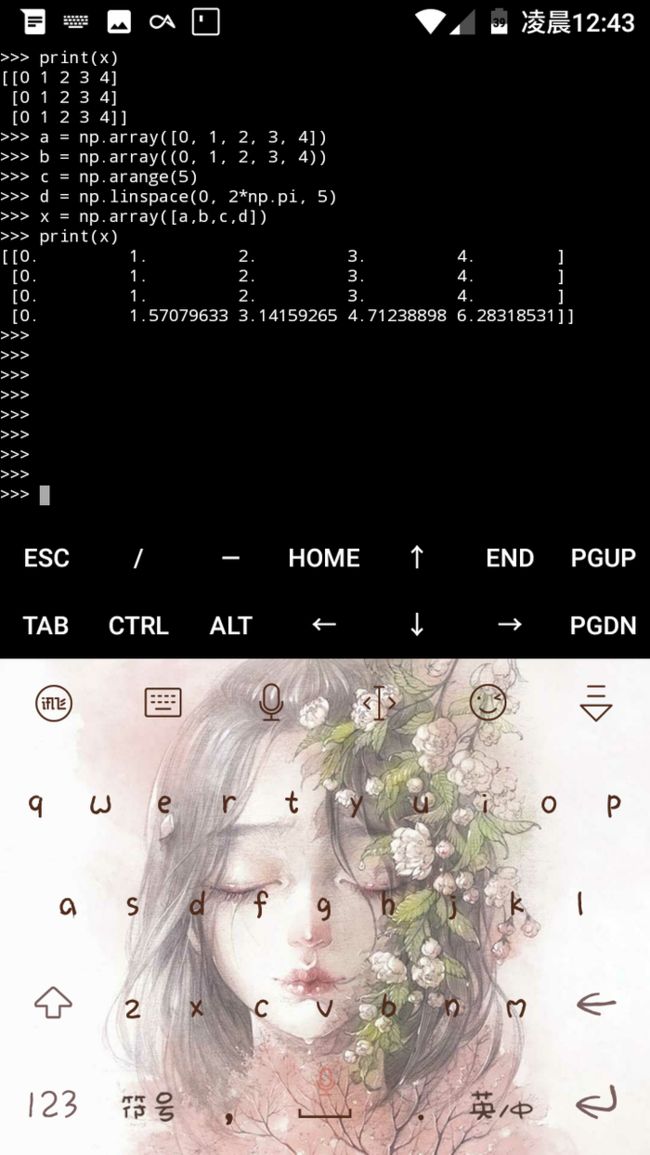
同理，我们可以搞一个二维数组

二维数组

注意，它会把数据统一成浮点数(所以看起来1,2,3,4后面都空了许多)，因此我们使用时应该注意

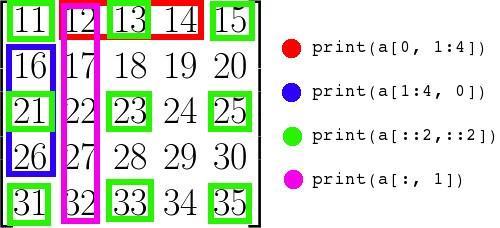
然后呢？切片我认为可能是不需要我说什么的了偷一个图过来可以说明一切

python教程1:numpy库

那么这些数组有哪些属性呢

如下，本人的执行过程

>>> import numpy as np

>>> what = np.array([[1,2,3],

... [6,5,4],

... [7,8,9]])

>>> print(what)

[[1 2 3]

[6 5 4]

[7 8 9]]

>>> print(type(what))

#n维数组

>>> print(what.dtype)

int64#数据类型

>>> print(what.shape)

(3, 3)#行数和列数

>>> print(what.size)

9#个数

>>> print(what.itemsize)

8#每个项占用字节数

>>> print(what.ndim)

2#数组z堆数

>>>print(what.nbytes)

72#总消耗字节数

其实的话，完整的构造方法应该如下

numpy.array(object, dtype = None, copy = True, order = None, subok = False, ndmin = 0)

object

数组或嵌套的数列

dtype

数组元素的数据类型，可选

copy

对象是否需要复制，可选

order

创建数组的样式，C为行方向，F为列方向，A为任意方向(默认)

subok

默认返回一个与基类类型一致的数组

ndmin

指定生成数组的最小维度

其实numpy内置了超级多的函数的，我因为numpy出了点问题，所以有些地方不演示了，介绍一下吧

numpy.char中就定义了许多函数，如下

函数

描述

add()

对两个数组的逐个字符串元素进行连接

multiply()

返回按元素多重连接后的字符串

center()

居中字符串

capitalize()

将字符串第一个字母转换为大写

title()

将字符串的每个单词的第一个字母转换为大写

lower()

数组元素转换为小写

upper()

数组元素转换为大写

split()

指定分隔符对字符串进行分割，并返回数组列表

splitlines()

返回元素中的行列表，以换行符分割

strip()

移除元素开头或者结尾处的特定字符

join()

通过指定分隔符来连接数组中的元素

replace()

使用新字符串替换字符串中的所有子字符串

decode()

数组元素依次调用str.decode

encode()

数组元素依次调用str.encode

这些函数和内置的差不多，只是操作对象不同

当然，怎么能少了数学计算？

NumPy 提供了标准的三角函数：sin()、cos()、tan()。

当然还有反三角函数

食用方法很简单，跳过

然而怎么能少了+-*/呢

NumPy 算术函数包含简单的加减乘除: add()，subtract()，multiply() 和 divide()。

需要注意的是数组必须具有相同的形状或符合数组广播规则。

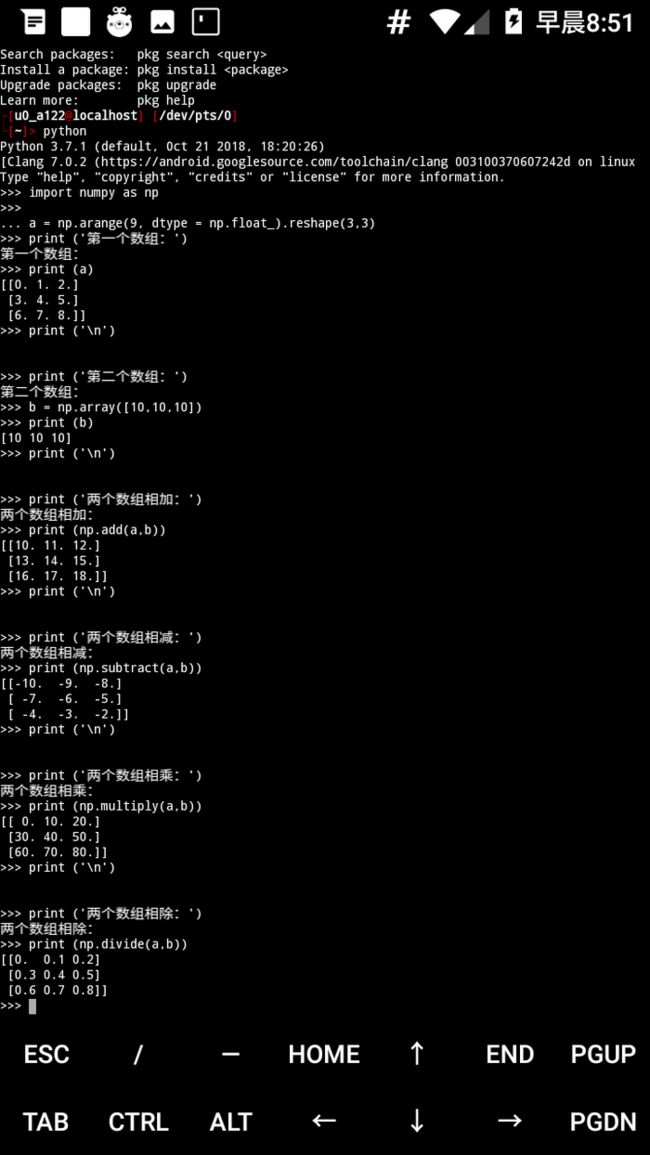
如图

数组的加减乘除

其实也就是一一对应相加

当然，还有很多呢

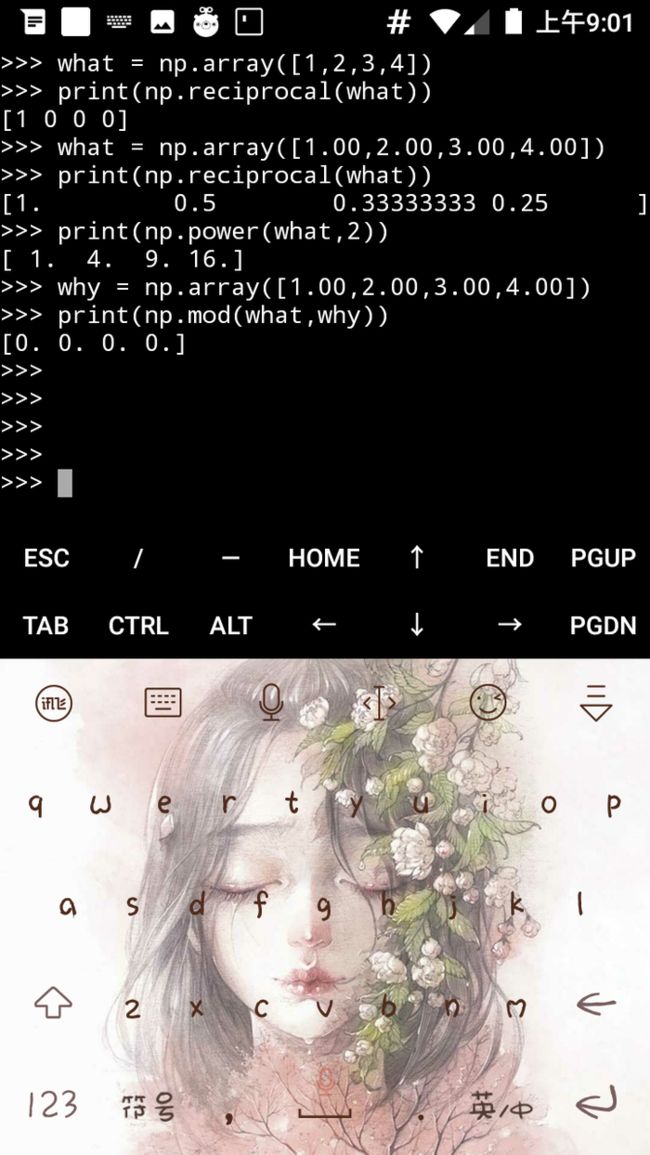
numpy.reciprocal() 函数返回参数逐元素的倒数。如 1/4 倒数为 4/1。

numpy.power() 函数将第一个输入数组中的元素作为底数，计算它与第二个输入数组中相应元素的幂。

numpy.mod() 计算输入数组中相应元素的相除后的余数。 函数 numpy.remainder() 也产生相同的结果。

一些操作函数

同时numpy还提供了超级多的用于统计的函数

参考这里

我不做介绍

numpy还提供了一个矩阵库

NumPy 中包含了一个矩阵库 numpy.matlib，该模块中的函数返回的是一个矩阵，而不是 ndarray 对象。

一个 的矩阵是一个由行(row)列(column)元素排列成的矩形阵列。

矩阵里的元素可以是数字、符号或数学式。

matlib.empty() 函数返回一个新的矩阵，语法格式为：

numpy.matlib.empty(shape, dtype, order)

shape: 定义新矩阵形状的整数或整数元组

Dtype: 可选，数据类型

order: C(行序优先) 或者 F(列序优先)

当然排序这些什么的我省略了，可以自行尝试

同时

NumPy 提供了线性代数函数库 linalg，该库包含了线性代数所需的所有功能

函数

描述

dot

两个数组的点积，即元素对应相乘。

vdot

两个向量的点积

inner

两个数组的内积

matmul

两个数组的矩阵积

determinant

数组的行列式

solve

求解线性矩阵方程

inv

计算矩阵的乘法逆矩阵

numpy.dot() 对于两个一维的数组，计算的是这两个数组对应下标元素的乘积和(数学上称之为内积)；对于二维数组，计算的是两个数组的矩阵乘积；对于多维数组，它的通用计算公式如下，即结果数组中的每个元素都是：数组a的最后一维上的所有元素与数组b的倒数第二位上的所有元素的乘积和：

dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])。

numpy.vdot() 函数是两个向量的点积。 如果第一个参数是复数，那么它的共轭复数会用于计算。 如果参数是多维数组，它会被展开。

numpy.inner() 函数返回一维数组的向量内积。对于更高的维度，它返回最后一个轴上的和的乘积。

…………懒惰的我决定省略留给你们探索

numpy i/o

Numpy 可以读写磁盘上的文本数据或二进制数据。

NumPy 为 ndarray 对象引入了一个简单的文件格式：npy。

npy 文件用于存储重建 ndarray 所需的数据、图形、dtype 和其他信息。

常用的 IO 函数有：

load() 和 save() 函数是读写文件数组数据的两个主要函数，默认情况下，数组是以未压缩的原始二进制格式保存在扩展名为 .npy 的文件中。

savze() 函数用于将多个数组写入文件，默认情况下，数组是以未压缩的原始二进制格式保存在扩展名为 .npz 的文件中。

loadtxt() 和 savetxt() 函数处理正常的文本文件(.txt 等)

numpy.save() 函数将数组保存到以 .npy 为扩展名的文件中。

食用方法

numpy.save(file, arr, allow_pickle=True, fix_imports=True)

参数说明：

file：要保存的文件，扩展名为 .npy，如果文件路径末尾没有扩展名 .npy，该扩展名会被自动加上。

arr: 要保存的数组

allow_pickle: 可选，布尔值，允许使用 Python pickles 保存对象数组，Python 中的 pickle 用于在保存到磁盘文件或从磁盘文件读取之前，对对象进行序列化和反序列化。

fix_imports: 可选，为了方便 Pyhton2 中读取 Python3 保存的数据。

numpy.savez() 函数将多个数组保存到以 npz 为扩展名的文件中。

numpy.savez(file, *args, **kwds)

参数说明：

file：要保存的文件，扩展名为 .npz，如果文件路径末尾没有扩展名 .npz，该扩展名会被自动加上。

args: 要保存的数组，可以使用关键字参数为数组起一个名字，非关键字参数传递的数组会自动起名为 arr_0, arr_1, …　。

kwds: 要保存的数组使用关键字名称。