快速排序算法（以int型数组为例）

快速排序的本质思想是分而治之

  一个待排序列，怎么 让它变得有序呢？我们先来看看一个有序的序列所具有的特征：当前指向的位置上的元素，一定不大于它右边位置的元素，也一定不小于它左边的元素，并且它的下标（秩），正是比他小的元素的数量

  就如箭头指向所指的已排序的数组其中的某个位置，该位置的值为5，不大于任何它右边位置的值，也不小于任何它左边的值。
  再考虑一下极端情况：如果数组的长度只有1，那这个数组本身就是有序的。

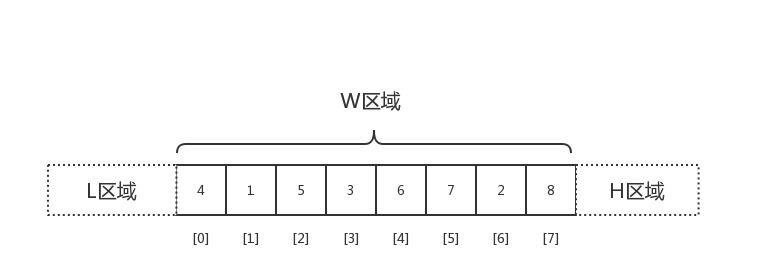
  那么如果我们随机选取了某一个元素，我们便可以将数组分为三个部分：

  最开始W区域就是未排序的整个数组，L和H区域是空的，紧接着我们在W区域中任意选取某一个元素，再将比它大的扔到右边，比他小的扔到左边，最后W区域退化成只有那个选定的元素存在的区域，长度为1，并且不难证明，此时该元素所在的位置，其实就是最后完全排序好后它的位置，利用反证法粗略证明如下：
  1.假设该元素做过上述变换以后所在的位置不是它最终排好序后的位置。
  2.比该位置小的元素都在它的L区域内，假设数量为N。
  3.该数组已排好序后，选取的那个元素具有的一个性质就是它左边的元素不大于它，其数量也就是N。
  4.那么就说明应该存在有两个位置，使得那两个位置左边的元素数量为N，显然不存在，产生矛盾，前提不成立。

我们来举个例子：

  这是一个数组的初始状态，我们的操作步骤是：
    1.取出a[0]中的元素作为我们选中的元素（称作轴点），用一个变量保存（可以形象地认为那个地方被挖空了）。
    2.我们从数组最后开始，即a[7],判断该位置元素大小，如果比轴点大，说明该元素本来就应该是H区域的元素，不需要调换，继续往左遍历，等到了a[6]时，值2 比轴点值 4小，应该是属于L区域的元素，此时a[0]是空的（想象）,我们就可以将这个值赋值到a[0]中，就相当于一个填坑动作，经过这个动作以后，a[6]这个位置就相当于是空的。
    3.经历过一次填坑动作以后，我们遍历的顺序就需要改变一下了，就要从a[0]开始往右遍历了（为了代码的简约易读），a[0]刚换过来的肯定是不大于轴点的，然后到a[1]，发现比轴点小，继续往右，到a[2],比轴点大，那么就应该进行一次填坑操作，将值a[6]赋值为5，此时a[2]变成了坑，遍历再次反转，注意！我们这次回到的位置是刚被填完坑的地方，即从a[6]开始往左遍历，循环往复。
    4.这一系例操作的终止标志应该是当左遍历撞上了右遍历，更精确的描述应该是:有两个指针 Lo , Hi ,分别指向数组最左端a[0],最右端a[7],并跟随着遍历移动，当 Lo < Hi 时，就一直反复执行上述步骤，直到这个条件被打破， 此时Lo 和 Hi 指向了相同的一个位置，这个位置非常特殊，因为这个位置是一个坑，我们用轴点的值来填补它，此时这个位置便就是我们选取的元素的最终位置。

  最终我们得到了这个结果，虽然它不是有序的，但是显然这距离完全有序迈进了一步，我们上面的一顿操作使这个数组产生了一些原来不一定存在的特性：

我们所选取的轴点已经到达了它最终的位置，L区域的所有元素不必轴点元素大，H区域的所有元素都不比轴点元素小。

  这是非常有用的信息，这意味着我们可以将产生的L区域和H区域当作一个新的更小规模的待排序数组，再次继续重复迭代地操作，每一次迭代，我们选取的那个区域的轴点元素，都可以找到它最终的位置，直到这个数组退化到本身就有序的单个元素的数组，将大问题转化成一个个子问题，并逐一解决，至此排序完成。

注意

  现在我们需要考虑这个轴点的选取问题，理想状态下我们当然是希望每次选取的这个轴点都是这组待排序列的中值（中位数），这样便可以均等划分L、H区间，这是最优的“分”策略，然而寻找中值所花费的代价是我们所不能忍受的，于是便退而求其次，采用一些较为好实现的方法。通常的办法有首、末选元法、随机选元法、三数中值分割法，

代码

  首先是快速排序的基本算法框架QuickSort()

typedef int Rank;

void QuickSort(int *t , Rank lo =0 , Rank hi = 10){
	if(hi - lo < 2) return; //递归基 如果hi和lo差距仅有1,即仅有一个元素的比对,直接返回
	Rank mid = partition(t,lo,hi-1); //在[lo,hi-1)之间构造轴点
	QuickSort(t,lo,mid);
	QuickSort(t,mid+1 ,hi);
}

  由此可以发现，快速排序算法耗费的时间绝大部分是来自分割函数partition()，除此之外的消耗仅占 o(1)的时间。

void swap(int *a ,int *b){
	int temp = *a ;
	*a = *b;
	*b = temp;
}


Rank partition(int *t, Rank lo , Rank hi){
	swap(&t[lo] , &t[lo+rand()%(hi-lo+1)]); //任选一个元素与首元素互换，保证选区的轴点不极端偏移
	int pivot = t[lo]; //选取转换后首元素为轴点
	while(lo < hi){
		//在每一次都要保证lo < hi的前提下，将比pivot大的元素放在它的右边，同理小的放左边 
		while((lo < hi) & (pivot <= t[hi])) {hi--;} t[lo] = t[hi];
		while((lo < hi) & (t[lo] <= pivot)) {lo++;} t[hi] = t[lo];  
	}
	t[lo] = pivot;
	return lo;
}

  上述寻找轴点的方式用的是随机选元法，还要注意一个小细节就是遍历时每一次头尾两个指针的移动都可能会造成 Lo < Hi 这个条件不成立，所以每一次遍历成功的前提就是需要满足这个条件。

进一步优化

 while(lo < hi){
        //在每一次都要保证lo < hi的前提下，将比pivot大的元素放在它的右边，同理小的放左边 
        while((lo < hi) & (pivot <= t[hi])) {hi--;} t[lo] = t[hi];
        while((lo < hi) & (t[lo] <= pivot)) {lo++;} t[hi] = t[lo];  
    }

  对于上述核心步骤，我们发现，如果数组是一个元素均重复的退化情况，就会造成最后分配的L区域和H区域的元素数量相差巨大（假设总数是N，第一次L区域有N-1个元素，H区域居然是空！！），更可怕的是，在后续迭代时，这种情况会一直存在，导致算法等效退化为线性递归，总体运行时间将高达o(n^2)，这是我们所不能接受的。

Rank partition(int *t, Rank lo , Rank hi){
	//优化部分
	swap(&t[lo] , &t[lo+rand()%(hi-lo+1)]); //任选一个元素与首元素互换，保证选区的轴点不极端偏移
	int pivot = t[lo]; //选取转换后首元素为轴点
	while(lo < hi){
		while(lo < hi){
			if(pivot < a[hi])
				hi--;
			else
				{a[lo++] = a[hi]; break;}
		}

		while(lo < hi){
			if(a[lo] < pivot)
				lo++;
			else
				{a[hi--] = a[lo]; break;}
		}
	}
	t[lo] = pivot;
	return lo;
}

  优化后的核心步骤中加了两个关键的break语句，使得就算是元素重复的完全退化数组，找到的轴点也必定在数组居中部位，并且每一次迭代都是如此。

复杂度

最坏情况下

假设虽然采用了一些寻找轴点的策略，但不走运的是每次找到的轴点均是当前待排数组的边界，则算法就如同未优化的partition函数遇到均是重复元素的退化数组一般，退化成线性递归，时间复杂度高达o(n^2)!!!

平均复杂度

当然，通常情况下我们可没这么倒霉，遇到上述情况的次数可以说是寥寥无几，而相应的，快速排序的平均复杂度是相当喜人的，可以达到o(nlogn),并且其时间复杂度中的常系数更小，例如，采用随机采元法的快速排序算法的平均效率是o(2ln2*logn),大约是o(1.386**logn)!! （具体数学推导方法参照清华大学邓俊辉著的《数据结构》第三版p339页）

完整代码加测试

#include 
#include 
#include 
typedef int Rank;


void swap(int *a ,int *b){
	int temp = *a ;
	*a = *b;
	*b = temp;
}


// Rank partition(int *t, Rank lo , Rank hi){
// 	swap(&t[lo] , &t[lo+rand()%(hi-lo+1)]); //任选一个元素与首元素互换，保证选区的轴点不极端偏移
// 	int pivot = t[lo]; //选取转换后首元素为轴点
// 	while(lo < hi){
// 		//在每一次都要保证lo < hi的前提下，将比pivot大的元素放在它的右边，同理小的放左边 
// 		while((lo < hi) & (pivot <= t[hi])) {hi--;} t[lo] = t[hi];
// 		while((lo < hi) & (t[lo] <= pivot)) {lo++;} t[hi] = t[lo];  
// 	}
// 	t[lo] = pivot;
// 	return lo;
// }	


Rank partition(int *t, Rank lo , Rank hi){
	//优化部分
	swap(&t[lo] , &t[lo+rand()%(hi-lo+1)]); //任选一个元素与首元素互换，保证选区的轴点不极端偏移
	int pivot = t[lo]; //选取转换后首元素为轴点
	while(lo < hi){
		while(lo < hi){
			if(pivot < t[hi])
				hi--;
			else
				{t[lo++] = t[hi]; break;}
		}

		while(lo < hi){
			if(t[lo] < pivot)
				lo++;
			else
				{t[hi--] = t[lo]; break;}
		}
	}
	t[lo] = pivot;
	return lo;
}	

 
void QuickSort(int *t , Rank lo =0 , Rank hi = 10){
	if(hi - lo < 2) return; //递归基 如果hi和lo差距仅有1,即仅有一个元素的比对
	Rank mid = partition(t,lo,hi-1); //在[lo,hi-1)之间构造轴点
	QuickSort(t,lo,mid);
	QuickSort(t,mid+1 ,hi);
}


void  getArray(int *a){
	srand((unsigned)time(NULL));
	for(int i = 0 ;  i < 10 ; i++){
		a[i] = rand()%100 + 1; 
	}
}

void printArray(int *a){
	int i = 0 ;
	while(i < 10){
		printf("%d ",a[i]);
		i++;
	}
	printf("\n");
}

int main(int argc, char const *argv[])
{
	int a[10];
	getArray(a);
	printf("未排序：\n");
	printArray(a);
	printf("已排序：\n");
	QuickSort(a);
	//QuickSort(a,0,10);
	printArray(a); 
	return 0;
}