二叉树——堆
目录
一.概念
二、特殊的二叉树
三、性质
四、二叉树的存储结构
五、堆的概念及结构
代码实现(以大堆为目的的代码)
堆的构建
堆的初始化
堆的摧毁
栈的数据交换
向上调整算法——在每次删除/加入数据后就会进行改变,保证大/小堆
堆的插入
堆的空判断
堆的删除
向下调整算法
返回堆的元素个数
取堆顶的数据
一.概念
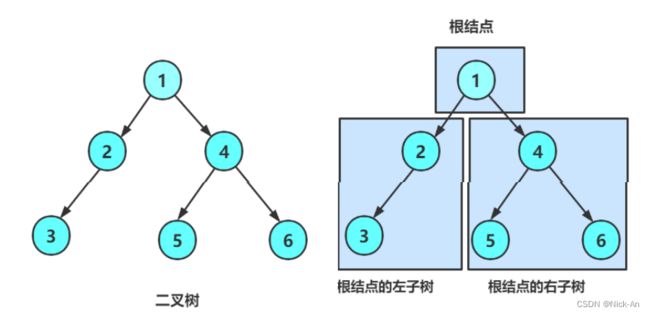
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
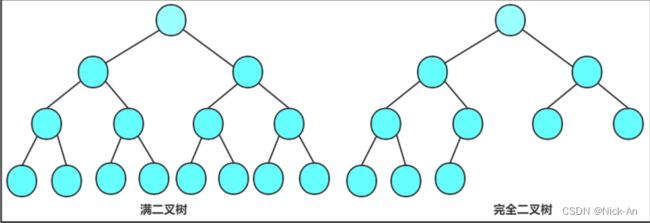
二、特殊的二叉树
满二叉树:如果一个二叉树的层数为K,且结点总数是2^k-1
完全二叉树:有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点
三、性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有(2^i)-1个结点.
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是(2^h)-1个.
3. 对任何一棵二叉树, 如果度为n0其叶结点个数为 , 度为n2的分支结点个数为 ,则有n0=n2+1
4. 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=log2(n+1)
(ps: 是log以2为底,n+1为对数)
四、二叉树的存储结构
1、顺序存储——用数组存放
2、链式存储——用指针指向
五、堆的概念及结构
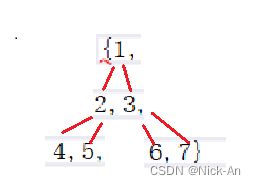
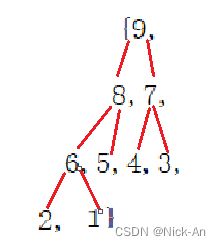
如果有一个关键码的集合K = {k0,k1,k2......km },把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足:Ki<=K(2*i+1) 且 Ki<= )K(2*i+2)(i = 0,1,2…,)则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
小堆:小的数据往上放——数组存放就是[1,2,3,4,5,6,7]
大堆:大的数据往上放——数组存放就是[9,8,7,6,5,4,3,2,1]
代码实现(以大堆为目的的代码,顺序存放)
堆的构建
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;//数组——二叉树可以形象地看做成一个树
int size;//大小
int capacity;//容量
}HP;堆的初始化
void HeapInit(HP* php)
{
assert(php);
php->a=NULL;
php->size=0;
php->capacity=0;
}堆的摧毁
void HeapDestory(Heap* php)
{
php->a=NULL;//置0,然后再对其进行释放
free(php->a);
php->size=0;
php->capacity=0;
}栈的数据交换
void Swap(HPDataType* p1, HPDataType* p2)
{
HPDataType* tmp=*p1;
*p1=*p2;
*p2=tmp;
}向上调整算法——在每次删除/加入数据后就会进行改变,保证大/小堆
是一个从子代——父代的过程
void AdjustUp(HPDataType* a, int child)//向上调整,就从子代开始
{
int parent=(child-1)/2;
while(child>0)
{
if(a[child]>a[parent])
{
Swap(&a[child],&a[parent]);
child=parent;//当前父代的位置赋值给子代,实现向上调整
parent=(child-1)/2;
}
else
{
break;//说明此时上边的都比子代大,则不需要往上调整了
}
}
}堆的插入
void HeapPush(Heap* php, HPDataType x)
{
assert(php);
if(php->size==php->capacity)
{
int newcapacity=capacity==0?4:capacity*2;//内存检查
HPDataType* tmp=(HPDataType*)realloc(php->a,sizeof(HPDataType)*newcapacity);
if(tmp==NULL)//若创建失败,就会显示错误信息并且结束进程
{
perror("realloc fail");
return ;
}
php->a=tmp;
php->capacity=newcapacity;
}
php->a[php->size]=x;
php->size++;
AdjustUp(php->a,php->size-1);
}堆的空判断
bool HeapEmpty(HP* php)
{
assert(php);
return php->size==0;
}堆的删除
由于若直接删除第一个元素,那么会对于整个堆结构有很大的影响,所以我们先实现堆中第一个元素与最后一个元素的交换,然后删除最后一个元素,再进行向下调整
void HeapPop(Heap* hp)
{
assert(php);
assert(!HeapEmpty(php));
Swap(&php->a[0],&php->a[php->size-1]);
php->size--;
AdjustDown(php->a,php->size,0);//向下调整的算法
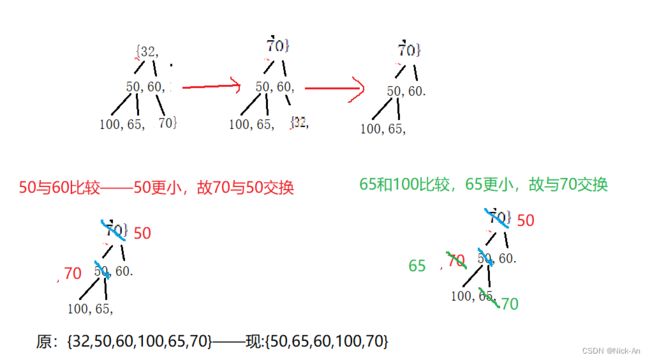
}向下调整算法(以删除顶部数据为例)
概念图(小端示例,大端仅相反比较即可)
是一个找出子代的最大/最小值,然后跟父代比较进行交换的过程
需要有元素个数/数组/需要调整的父代的位置(向下则是从父代——子代的过程)
void AdjustDown(int *a, int n, int parent)
{
int child=parent*2+1;//默认一个最小的左孩子
while(childa[child])
{
++child;//此时,子代最大值的下标需要改变
}
if(a[child]>a[parent])//若子代大于父代,说明需要交换
{
Swap(&a[child],&a[parent]);
parent=child;//此时继续往下
child=parent*2+1; //继续往下
}
else
{
break;
}
}
} 返回堆的元素个数
int HeapSize(HP* php)
{
assert(php);
assert(!HeapEmpty(php));
return php->size
}取堆顶的数据
HPDataType HeapTop(HP* php)
{
assert(php);
assert(!HeapEmpty(php));
return php->a[0];
}大堆/小堆的实现,仅需要改变向上/向下调整内子代与父代的大小关系即可