【PyTorch】多层感知机
文章目录
- 1. 模型与代码实现
-
- 1.1. 模型
-
- 1.1.1. 背景
- 1.1.2. 多层感知机
- 1.1.3. 激活函数
- 1.2. 代码实现
-
- 1.2.1. 完整代码
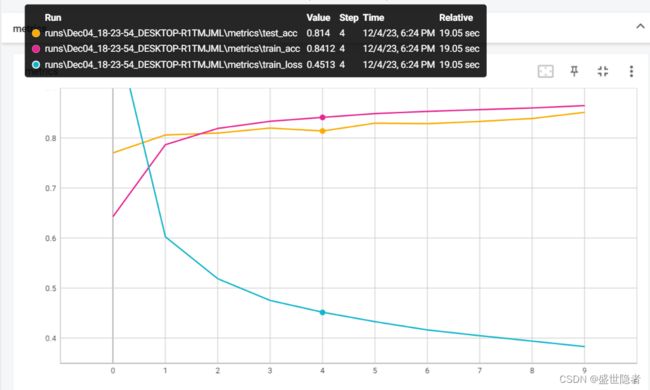
- 1.2.2. 输出结果
- 2. Q&A
1. 模型与代码实现
1.1. 模型
1.1.1. 背景
许多问题要使用线性模型,但无法简单地通过预处理来实现。此时我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制, 使其能处理更普遍的函数关系类型。
1.1.2. 多层感知机
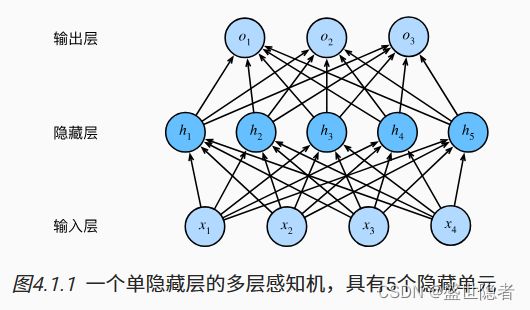
将许多全连接层堆叠在一起。 每一层都输出到上面的层,直到生成最后的输出,我们可以把前层看作表示,把最后一层看作线性预测器。 这种架构通常称为多层感知机,通常缩写为MLP。
1.1.3. 激活函数
我们需要在仿射变换之后对每个隐藏单元应用非线性的激活函数,这样就不可能再将我们的多层感知机退化成线性模型,使得模型具有更强的表达能力。
激活函数是通过计算加权和并加上偏置来确定神经元是否应该被激活, 并将输入信号转换为输出的可微运算的函数。
-
ReLU函数
-
修正线性单元(Rectified linear unit,ReLU)。
-
最受欢迎的激活函数。
-
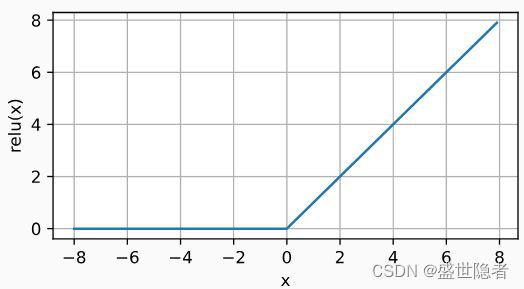
定义: R e L U ( x ) = m a x ( 0 , x ) \mathrm{ReLU}(x)=\mathrm{max}(0,x) ReLU(x)=max(0,x)
-
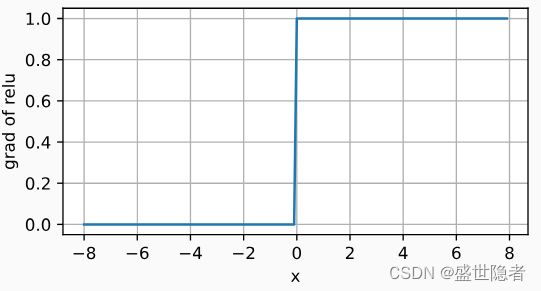
当输入值精确等于0时,ReLU函数不可导。 在此时,我们默认使用左侧的导数,即当输入为0时导数为0。 我们可以忽略这种情况,因为输入可能永远都不会是0。
-
变体:参数化的ReLU(Parameterized ReLU,pReLU),允许即使参数是负的,某些信息依然可以通过,其定义如下: p R e L U ( x ) = m a x ( 0 , x ) + α m i n ( 0 , x ) \mathrm{pReLU}(x)=\mathrm{max}(0,x)+\alpha\mathrm{min}(0,x) pReLU(x)=max(0,x)+αmin(0,x)等等。
-
-
sigmoid函数
-
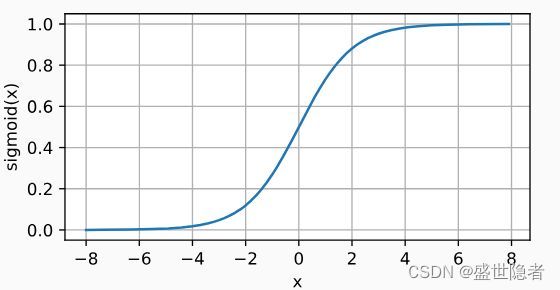
将输入变换为区间(0, 1)上的输出。
-
在隐藏层中已经较少使用, 它在大部分时候被更简单、更容易训练的ReLU所取代。
-
定义: s i g m o i d ( x ) = 1 1 + e x p ( − x ) \mathrm{sigmoid}(x)=\frac{1}{1+\mathrm{exp}(-x)} sigmoid(x)=1+exp(−x)1
-
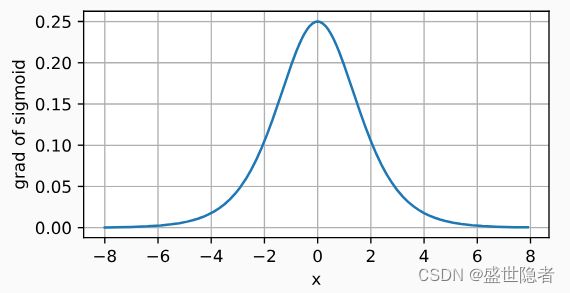
导数: d d x s i g m o i d ( x ) = s i g m o i d ( x ) ( 1 − s i g m o i d ( x ) ) \frac{\mathrm{d}}{\mathrm{d}x}\mathrm{sigmoid}(x)=\mathrm{sigmoid}(x)(1-\mathrm{sigmoid}(x)) dxdsigmoid(x)=sigmoid(x)(1−sigmoid(x))
-
-
tanh函数
-
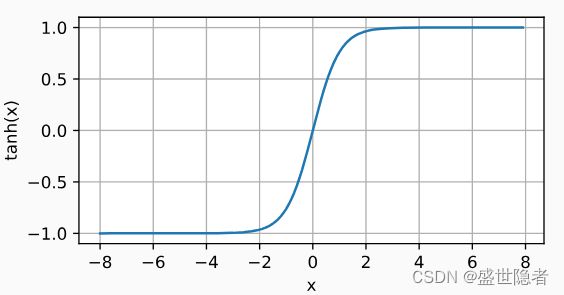
将其输入压缩转换到区间(-1, 1)上。
-
定义: t a n h ( x ) = 1 − e x p ( − 2 x ) 1 + e x p ( − 2 x ) \mathrm{tanh}(x)=\frac{1-\mathrm{exp}(-2x)}{1+\mathrm{exp}(-2x)} tanh(x)=1+exp(−2x)1−exp(−2x)
-
当输入接近0时,tanh函数接近线性变换。
-
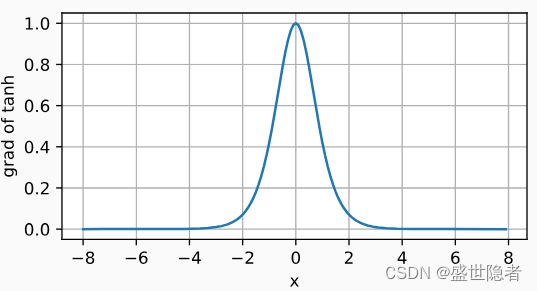
导数: d d x t a n h ( x ) = 1 − t a n h 2 ( x ) \frac{\mathrm{d}}{\mathrm{d}x}\mathrm{tanh}(x)=1-\mathrm{tanh}^2(x) dxdtanh(x)=1−tanh2(x)
-
1.2. 代码实现
1.2.1. 完整代码
import torch
from torchvision import transforms
from torchvision.datasets import FashionMNIST
from torch.utils.data import DataLoader
from torch import nn
from tensorboardX import SummaryWriter
def load_dataset(batch_size, num_workers):
"""加载数据集"""
root = "./dataset"
transform = transforms.Compose([transforms.ToTensor()])
mnist_train = FashionMNIST(
root=root,
train=True,
transform=transform,
download=True
)
mnist_test = FashionMNIST(
root=root,
train=False,
transform=transform,
download=True
)
dataloader_train = DataLoader(
mnist_train,
batch_size,
shuffle=True,
num_workers=num_workers
)
dataloader_test = DataLoader(
mnist_test,
batch_size,
shuffle=False,
num_workers=num_workers
)
return dataloader_train, dataloader_test
def init_network(net):
"""初始化模型参数"""
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, mean=0, std=0.01)
nn.init.constant_(m.bias, val=0)
if isinstance(net, nn.Module):
net.apply(init_weights)
class Accumulator:
"""在n个变量上累加"""
def __init__(self, n):
self.data = [0.0] * n
def add(self, *args):
self.data = [a + float(b) for a, b in zip(self.data, args)]
def reset(self):
self.data = [0.0] * len(self.data)
def __getitem__(self, idx):
return self.data[idx]
def accuracy(y_hat, y):
"""计算预测正确的数量"""
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
y_hat = y_hat.argmax(axis=1)
cmp = y_hat.type(y.dtype) == y
return float(cmp.type(y.dtype).sum())
def train(net, dataloader_train, criterion, optimizer, device):
"""训练模型"""
if isinstance(net, nn.Module):
net.train()
train_metrics = Accumulator(3) # 训练损失总和、训练准确度总和、样本数
for X, y in dataloader_train:
X, y = X.to(device), y.to(device)
y_hat = net(X)
loss = criterion(y_hat, y)
optimizer.zero_grad()
loss.mean().backward()
optimizer.step()
train_metrics.add(float(loss.sum()), accuracy(y_hat, y), y.numel())
train_loss = train_metrics[0] / train_metrics[2]
train_acc = train_metrics[1] / train_metrics[2]
return train_loss, train_acc
def test(net, dataloader_test, device):
"""测试模型"""
if isinstance(net, nn.Module):
net.eval()
with torch.no_grad():
test_metrics = Accumulator(2) # 测试准确度总和、样本数
for X, y in dataloader_test:
X, y = X.to(device), y.to(device)
y_hat = net(X)
test_metrics.add(accuracy(y_hat, y), y.numel())
test_acc = test_metrics[0] / test_metrics[1]
return test_acc
if __name__ == "__main__":
# 全局参数设置
batch_size = 256
num_workers = 4
num_epochs = 10
learning_rate = 0.1
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 创建记录器
writer = SummaryWriter()
# 加载数据集
dataloader_train, dataloader_test = load_dataset(batch_size, num_workers)
# 定义神经网络
net = nn.Sequential(
nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10)
).to(device)
# 初始化神经网络
init_network(net)
# 定义损失函数
criterion = nn.CrossEntropyLoss(reduction='none')
# 定义优化器
optimizer = torch.optim.SGD(net.parameters(), lr=learning_rate)
for epoch in range(num_epochs):
train_loss, train_acc = train(net, dataloader_train, criterion, optimizer, device)
test_acc = test(net, dataloader_test, device)
writer.add_scalars("metrics", {
'train_loss': train_loss,
'train_acc': train_acc,
'test_acc': test_acc
},
epoch)
writer.close()