Gmsh <一>:Geometric model construction
Gmsh的python接口使用pip命令即可安装,利用其提供的函数接口,可以构建几何模型和生成相应的网格。
pip install gmsh
Gmsh中有两个几何内核用于构造几何,一个是内置的 built-in 几何内核 (geo),另一个是第三方的 OCC 内核,其中build-in内核仅支持自下而上构建几何体,即以点-线-边-面的顺序逐步构建几何;OCC内核不仅支持自下而上构建几何,同时还支持使用建模函数来构建几何体。
在gmsh脚本中,每一个几何实体(点,线,面等)都会被分配到一个label(编号),可以手动定义,不然系统则按顺序进行编号。相同类型的几何实体的编号必须是不同的,例如不能有两个编号都是2的点或线。在Python中由于调用生成几何实体的函数返回的值就是编号,所以将这些实体进行变量名命名(点可以用p1,p2,…命名,线可以用l1,l2,…),这样就避免了对编号是否唯一的检查。
Built-in 内核
使用 Gmsh 的 Python API,首先导入 gmsh 模块
import gmsh
若想使用 gmsh,需要先对其进行初始化,使用初始化命令
gmsh.initialize() # 使用gmsh前需要进行初始化
之后,我们创建一个模型
gmsh.model.add("model1")
自下而上创建几何对象,首先需要构建点对象
gmsh.model.geo.addPoint(0, 0, 0, 0.1, 1)
gmsh.model.geo.addPoint(1, 0, 0, 0.1, 2)
gmsh.model.geo.addPoint(1, 1, 0, 0.1, 3)
gmsh.model.geo.addPoint(0, 1, 0, 0.1, 4)
其中前三个参数是点的坐标,gmsh的几何是在三维下创建的,若想创建二维几何,则将坐标z轴即第三个参数设置为0即可。第四个参数为该点处的网格尺寸值,第五个参数为该点的编号,若不写则默认从1开始计,该处不写效果一样。
创建完点,创建线
gmsh.model.geo.addLine(1, 2, 1)
gmsh.model.geo.addLine(3, 2, 2)
gmsh.model.geo.addLine(3, 4, 3)
gmsh.model.geo.addLine(4, 1, 4)
前两个参数是点的标号,即边的两个端点的标号,同时还定义了线的方向,即从第一个点指向第二个点,第三个是参数是编号,与定义点的编号的用法一致,注意,不同类型的几何实体的标号是不通用的,即给点定义了编号1到4后,同样可以给线定义1到4,相同的几何实体编号不能重复。
之后,我们需要创建边对象和面对象
gmsh.model.geo.addCurveLoop(1, -2, 3, 4)
gmsh.model.geo.addPlaneSurface([1], 1)
想要生成面,首先需要创建边对象,也称为线环、闭合曲线循环(CurveLoop),则将线组成闭合曲线循环,其中第一个变量为一个列表,里面按顺序放置组成边界的线的编号,线之间必须首尾相连,由于2号线的方向是从3号点指向2号点,所以在2前面添一个负号,表示其相反方向,第二个参数为边的编号。
创建完边对象后,便可以创建面对象,其中第一个参数是存放边对象的编号的列表,第二个参数为面的编号。
当我们创建完一个几何对象后,我们将上面的设置同步到我们创建的模型,生成二维网格并将网格数据输出到.msh文件或者.off文件
gmsh.model.geo.synchronize() # 同步到模型
gmsh.model.mesh.generate(2) # 生成网格
gmsh.write("model1.msh") # 生成.msh文件 .msh改为.off则生成.off文件
其中,第二行的代码generate(2)中的参数2是2维的意思,二维平面生成网格则输入2,三维图形生成面网格输入2,生成体网格则输入3。
最后,在图形界面显示结果,并结束使用gmsh
gmsh.fltk.run() # 图形界面显示
gmsh.finalize() # 结束使用gmsh
这样就完成了一个简单的二维正方形的几何创建和网格生成。
完整代码如下:
import gmsh
gmsh.initialize() # 初始化
gmsh.model.add("model1") # 创建模型
lc = 1e-1 # 设置网格尺寸值
# 创建点
gmsh.model.geo.addPoint(0, 0, 0, lc, 1)
gmsh.model.geo.addPoint(1, 0, 0, lc, 2)
gmsh.model.geo.addPoint(1, 1, 0, lc, 3)
gmsh.model.geo.addPoint(0, 1, 0, lc, 4)
#创建线
gmsh.model.geo.addLine(1, 2, 1)
gmsh.model.geo.addLine(3, 2, 2)
gmsh.model.geo.addLine(3, 4, 3)
gmsh.model.geo.addLine(4, 1, 4)
# 创建边
gmsh.model.geo.addCurveLoop([4, 1, -2, 3], 1)
# 创建面
gmsh.model.geo.addPlaneSurface([1])
gmsh.model.geo.synchronize() # 同步到模型
gmsh.model.mesh.generate(2) # 生成网格
gmsh.write("model1.msh") # 生成.msh文件
gmsh.fltk.run() # 图形界面显示
gmsh.finalize() # 关闭gmsh
结果如下:
当然,我们还可以在二维几何体的中间进行挖空,
代码如下:
import gmsh
gmsh.initialize()
gmsh.model.add("model2")
lc = 5e-2
# 构建几何
gmsh.model.geo.addPoint(0, 0, 0, lc, 1)
gmsh.model.geo.addPoint(1, 0, 0, lc, 2)
gmsh.model.geo.addPoint(1, 1, 0, lc, 3)
gmsh.model.geo.addPoint(0, 1, 0, lc, 4)
gmsh.model.geo.addLine(1, 2, 1)
gmsh.model.geo.addLine(3, 2, 2)
gmsh.model.geo.addLine(3, 4, 3)
gmsh.model.geo.addLine(4, 1, 4)
gmsh.model.geo.addPoint(0.5, 0.5, 0, lc, 5)
gmsh.model.geo.addPoint(0.3, 0.5, 0, lc, 6)
gmsh.model.geo.addPoint(0.7, 0.5, 0, lc, 7)
# 构建圆弧(线)
gmsh.model.geo.addCircleArc(6, 5, 7, 5)
gmsh.model.geo.addCircleArc(7, 5, 6, 6)
gmsh.model.geo.addCurveLoop([4, 1, -2, 3], 1)
gmsh.model.geo.addCurveLoop([5,6], 2)
gmsh.model.geo.addPlaneSurface([1,2], 1)
# gmsh.model.geo.addPlaneSurface([2], 2)
gmsh.model.geo.synchronize()
gmsh.model.mesh.generate(2)
gmsh.fltk.run()
gmsh.finalize()
在这段代码中有个新函数,addCircleArc(),其中第一个参数是起始点的编号,第二个参数是圆心点的编号,第三个参数是终止点的编号(弧度为 π \pi π时逆时针优先),以此来创建一个弧度不超过 π \pi π的圆弧(几何类型属于线),调用两次该函数,圆心不变,起始点和终止点互换,创建了两个圆弧从而可以拼接出一个首尾相接的圆。

在构建面对象时,所用的边列表为[1, 2],边1为外边界,边2为内部的洞边界,Gmsh默认列表的第一个边记号为外边界,之后的边都为内部的洞边界。如果我们想生成界面网格,只需把洞也构建成一个面对象,即去掉 gmsh.model.geo.addPlaneSurface([2], 2) 的注释即可,效果如下:

当然,采用geo自下而上构造几何的方法,我们同样可以创建三维网格模型,代码如下:
import gmsh
gmsh.initialize() # 初始化Gmsh
gmsh.model.add("model4") # 创建模型
# lc = 2e-1
# 创建点
gmsh.model.occ.addPoint(0, 0, 0)
gmsh.model.occ.addPoint(1, 0, 0)
gmsh.model.occ.addPoint(1, 1, 0)
gmsh.model.occ.addPoint(0, 1, 0)
gmsh.model.occ.addPoint(0, 0, 1)
gmsh.model.occ.addPoint(1, 0, 1)
gmsh.model.occ.addPoint(1, 1, 1)
gmsh.model.occ.addPoint(0, 1, 1)
# 创建线
gmsh.model.occ.addLine(1, 2)
gmsh.model.occ.addLine(2, 3)
gmsh.model.occ.addLine(3, 4)
gmsh.model.occ.addLine(4, 1)
gmsh.model.occ.addLine(5, 6)
gmsh.model.occ.addLine(6, 7)
gmsh.model.occ.addLine(7, 8)
gmsh.model.occ.addLine(8, 5)
gmsh.model.occ.addLine(1, 5)
gmsh.model.occ.addLine(2, 6)
gmsh.model.occ.addLine(3, 7)
gmsh.model.occ.addLine(4, 8)
# 创建线环(边)
gmsh.model.occ.addCurveLoop([1, 2, 3, 4])
gmsh.model.occ.addCurveLoop([5, 6, 7, 8])
gmsh.model.occ.addCurveLoop([1, 10, -5, -9])
gmsh.model.occ.addCurveLoop([2, 11, -6, -10])
gmsh.model.occ.addCurveLoop([3, 12, -7, -11])
gmsh.model.occ.addCurveLoop([4, 9, -8, -12])
# 创建面
gmsh.model.occ.addPlaneSurface([1])
gmsh.model.occ.addPlaneSurface([2])
gmsh.model.occ.addPlaneSurface([3])
gmsh.model.occ.addPlaneSurface([4])
gmsh.model.occ.addPlaneSurface([5])
gmsh.model.occ.addPlaneSurface([6])
# 创建面环
gmsh.model.occ.addSurfaceLoop([1, 2, 3, 4, 5, 6])
# 创建体
gmsh.model.occ.addVolume([1])
gmsh.model.occ.synchronize() #同步
# gmsh.model.mesh.generate(2) # 生成二维网格(面网格)
# gmsh.model.mesh.generate(3) # 生成三维网格(体网格)
gmsh.fltk.run() # 图形界面显示
gmsh.finalize() # 关闭gmsh
上述代码篇幅较长,我省略了编号的参数(gmsh中创建几何对象的编号参数都可以省略)。
与创建二维网格相比,除了在点和边维度上有拓展外,还需要新定义两样东西,面环和体,对应的函数分布为 addSurfaceLoop 和 addVolume 与定义线环和面类似,其参数分别为面列表和面环列表。
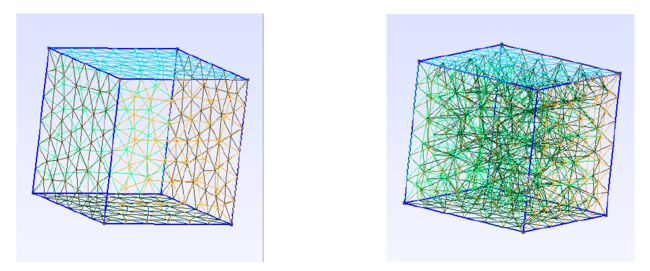
定义体的目的在于生成体网格,上面说过 generate 的参数是维度,现在我们对这个函数进行测试,分别将 gmsh.model.mesh.generate(2) 和 gmsh.model.mesh.generate(3) 注释,便可得到三维图形的面网格和体网格。
效果如下:
OCC内核
除了使用built-in内核来创建几何,我们还可以使用OCC内核来创建几何,OCC也支持自下而上构建几何,在上面代码中,把 gmsh.model.geo 改为 gmsh.model.occ 即可。除此以外,OCC支持以函数直接生成几何。
二维图形我们以创建矩形为例,代码如下:
import gmsh
gmsh.initialize()
gmsh.model.add("model5a")
gmsh.model.occ.addRectangle(0, 0, 0, 1, 1)
gmsh.model.occ.synchronize()
gmsh.model.mesh.setSize(gmsh.model.getEntities(0), 0.1)
gmsh.model.mesh.generate(2)
gmsh.fltk.run()
gmsh.finalize()
三维图形我们以创建立方体为例,代码如下:
import gmsh
gmsh.initialize()
gmsh.model.add("model5b")
gmsh.model.occ.addBox(0, 0, 0, 1, 1, 1, 1)
gmsh.model.occ.synchronize()
gmsh.model.mesh.setSize(gmsh.model.getEntities(0), 0.2)
gmsh.model.mesh.generate(2)
gmsh.fltk.run()
gmsh.finalize()
在上面的代码中,使用函数 addRectangle 可以构建矩形对象,前三个参数是矩形左下角点的坐标,第四个,第五个参数分别是矩形的长和高,第六个是编号。类似的,addBox 的前三个参数和最后一个参数作用相同,第四个,第五个,第六个参数则是立方体的长,宽,高。
由于不是自下而上构建几何,不能逐点去设置网格的尺寸值,因此使用 gmsh.model.getEntities 来获得所有点对象。若不输入任何参数,则该函数表示获得所有实体,若输入 0,则获取所有点对象,输入大于 0 的整数,表示获取所有该维度下的对象。之后,使用函数
gmsh.model.occ.setSize 来对所有点对象赋予网格尺寸值。
OCC 提供了许多函数来构建几何对象,除了addRectangle 和 addBox ,还有构造圆形的 addDisk,构造球的 addSphere 等等。
结果如下:
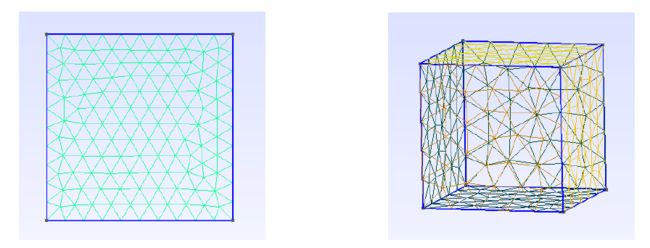
经过对比前面的网格模型后不难发现,model1与model5,model4与model6一致,而二者区别在于前者几何是用geo的自下而上方法构建,后者几何是用occ的函数构建,共同的在于边长一致,所有点的网格尺寸值一致,所以生成的网格一致。
接下来我们介绍布尔运算,同时使用这些基本的构建几何函数来构建更为复杂的几何模型。首先构造两个矩形,一个椭圆,一个圆
gmsh.model.occ.addRectangle(-1, -1, 0, 2, 2, 1)
gmsh.model.occ.addRcetangle(0, -1, 0, 1, 1, 2)
gmsh.model.occ.addDisk(0.5, 0.5, 0, 0.3, 0.2, 3)
gmsh.model.occ.addDisk(-0.5, -0.5, 0, 0.2, 0.2, 4)
其中,addDisk 函数可以用来构建一个圆或者椭圆,前三个参数为圆心的坐标,后两个参数分别为x方向和y方向的半径。我们想构建一个有椭圆的L型区域,因此我们使用布尔差运算
gmsh.model.occ.cut([(2, 1)], [(2, 2), (2, 3)], 5)
cut 函数的作用是计算几何体之间的差,并构建出新的几何体,第一个参数为布尔差的被减项,第二个参数为布尔差的减项,均为列表形式,列表中的每一个元素表示一个几何对象,在Python中,gmsh的几何对象使用元组表示,元组的第一个元素为几何对象的维数,第二个元素为几何对象的编号,因此 (2,1) 就表示标号为 1 的面;第三项为新生成几何对象的标号。上面函数的作用即为面 1 减去面 2 与面 3 所在的区域。默认情况下,使用 cut 函数后,使用的对象会被删除,即面 1,面 2,面 3 都会被删除,只保留面 4,如果想保留,则可以设置第五个与第六个参数为 False。
我们还想在区域内构造一个圆形的界面,因此使用 fragment 函数
gmsh.model.occ.fragment([(2, 4)], [(2, 5)])
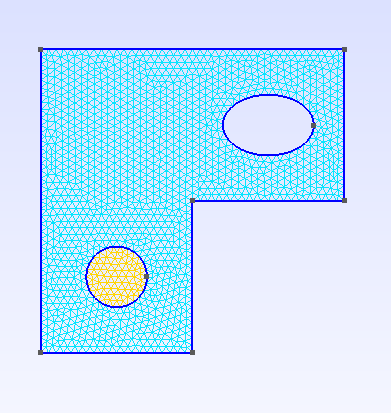
类似于 cut 函数,第一,第二个参数为包含几何对象的列表,fragment 函数的作用将输入的几何对象进行组合,下面的结果中可以看到,圆形区域界面嵌入了L形区域中。像这样在复杂几何体内部生成网格的技术,也叫做贴体网格。
完整代码如下:
import gmsh
gmsh.initialize()
gmsh.model.add("model6")
# 构建几何
gmsh.model.occ.addRectangle(-1, -1, 0, 2, 2, 1)
gmsh.model.occ.addRectangle(0, -1, 0, 1, 1, 2)
gmsh.model.occ.addDisk(0.5, 0.5, 0, 0.3, 0.2, 3)
gmsh.model.occ.addDisk(-0.5, -0.5, 0, 0.2, 0.2, 4)
# 作布尔差
gmsh.model.occ.cut([(2, 1)], [(2, 2), (2, 3)], 5)
# 合并
gmsh.model.occ.fragment([(2, 4)], [(2, 5)])
gmsh.model.occ.synchronize()
gmsh.model.mesh.setSize(gmsh.model.getEntities(0), 0.05)
gmsh.model.mesh.generate(2)
gmsh.fltk.run()
gmsh.finalize()
结果如下:
用方程生成几何
前面了解了 Gmsh 构造几何的两个几何内核(geo 和 occ),现在我们采用OCC自下而上的思想,从点,线,面,体依次递进,创建以顶点坐标,极坐标,参数方程,球坐标为参数,生成对应图形几何网格的API,并附带测试文件测试下列函数:
参数方程1:
x = ( 2 + c o s k t ) ⋅ c o s t x = (2 + cos kt) · cost x=(2+coskt)⋅cost
y = ( 2 + c o s k t ) ⋅ s i n t y = (2 + cos kt) · sin t y=(2+coskt)⋅sint
参数方程2:
x = 16 sin 3 t x = 16 \sin^3 t x=16sin3t
y = 13 cos t − 5 cos 2 t − 2 cos 3 t − cos 4 t y = 13 \cos t - 5 \cos 2t - 2 \cos 3t - \cos 4t y=13cost−5cos2t−2cos3t−cos4t
极坐标方程:
ρ = 0.7 ⋅ ( 1 − sin 2 θ ) \rho = 0.7 \cdot (1 - \sin^2 \theta) ρ=0.7⋅(1−sin2θ)
ρ = 1.0 + 0.2 ⋅ sin 5 θ \rho = 1.0 + 0.2 \cdot \sin5 \theta ρ=1.0+0.2⋅sin5θ
球坐标方程:
ρ = 2 \rho = 2 ρ=2
ρ = 0.2 + 0.05 ⋅ ( 1 / 8 ⋅ ( 35 ⋅ cos 4 θ − 30 ⋅ c o s 2 θ + 3 ) ) \rho = 0.2 + 0.05 \cdot (1/8 \cdot (35 \cdot \cos^4 \theta - 30 \cdot cos^2 \theta + 3)) ρ=0.2+0.05⋅(1/8⋅(35⋅cos4θ−30⋅cos2θ+3))
首先,我们配置包和定义网格尺寸值(网格尺寸值作为函数的参数更合理,这里为了方便演示提前定义好网格尺寸值)
import gmsh
import math
import numpy as np
# 网格尺寸值
lc = 2e-1
之后,我们开始创建API
以顶点坐标为参数的API(二维)
# 用顶点坐标生成网格
# p: 二维顶点坐标组成的列表
def model_made_point(p):
# 创建点
points = [gmsh.model.occ.addPoint(*pt, 0, lc) for pt in p]
# 将点按顺序依次连接,创建线(形成闭合图形)
lines = [gmsh.model.occ.addLine(points[i-1], points[i]) for i in range(len(points))]
# 创建线环
cloop = gmsh.model.occ.addCurveLoop(lines)
# 创建面
face = gmsh.model.occ.addPlaneSurface([cloop])
return face
测试文件代码:
import gmsh
import gmsh_occ_tools as tools
gmsh.initialize()
gmsh.model.add("model7")
# 顶点坐标(二维,形如(x, y))(列表坐标的顺序需要符合首尾相连的顺序)
p = [[4, 7], [5, 5], [7, 5], [5, 3.5], [6, 1.5],
[4, 2.5], [2, 1.5], [3, 3.5], [1, 5], [3, 5]]
# 由给定的顶点坐标生成网格 (p为二维坐标列表)
model1 = tools.model_made_point(p)
gmsh.model.occ.synchronize() # 同步
gmsh.model.mesh.generate(2) # 生成网格
gmsh.fltk.run() # 图形界面显示
gmsh.finalize() # 关闭gmsh
在上述代码中,我们定义了二维坐标列表,其中每个坐标的数据形式是列表[x, y], 之后调用要测试的函数: model_made_point,通过给定的顶点坐标生成网格。
效果如下:
以极坐标方程为参数的API
# 用极坐标生成网格
# g: 极坐标方程的函数
# a, b: theta的左右边界(默认为[0, 2*pi])
# num: 均匀间隔点的个数
def model_made_polar(g, num, a=0, b=2 * math.pi):
# 计算定义域范围内的x坐标和y坐标的值
theta = np.linspace(a, b, num)
p = g(theta)
x = np.cos(theta) * p
y = np.sin(theta) * p
# 创建点
points = [gmsh.model.occ.addPoint(x[i], y[i], 0) for i in range(len(x))]
# 将点按顺序依次连接,创建线(形成闭合图形)
lines = [gmsh.model.occ.addLine(points[i], points[i + 1]) for i in range(len(points) - 1)]
# 创建线环
cloop = gmsh.model.occ.addCurveLoop(lines)
# 创建面
face = gmsh.model.occ.addPlaneSurface([cloop])
return face
测试文件代码:
import gmsh
import gmsh_occ_tools as tools
import numpy as np
gmsh.initialize()
gmsh.model.add("model8")
# 均匀间隔点的个数
num = 100
# 定义极坐标 g(x) = c * (1 - sin(x)) 返回形式为极长(点到极点的距离)的值
def g(x):
c = 0.7
rho = c * (1 - np.sin(x))
return rho
# # 定义极坐标 g(x) = 1.0 + 0.2 * sin(5x)
# def g(x):
# c = 1.0
# d = 0.2
# rho = c + d * np.sin(5 * x)
# return rho
# 由给定的极坐标生成网格 (g为极坐标,a ,b 为定义域边界)
model = tools.model_made_polar(g, num)
gmsh.model.occ.synchronize() # 同步
gmsh.model.mesh.generate(2) # 生成网格
gmsh.fltk.run() # 图形界面显示
gmsh.finalize() # 关闭gmsh
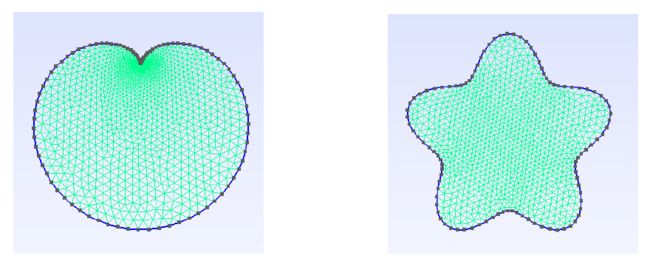
上述代码中,我们定义了两个极坐标方程,其中一个是著名的笛卡尔爱心曲线,另一个是生成一朵花状的曲线,之后调用要测试的函数model_made_polar,通过给定极坐标方程来生成网格。
效果如下:
以参数方程为参数的API
# 用参数方程生成网格
# f: 参数方程函数
# a, b: 参数的左右边界
# num: 均匀间隔点的个数
def model_made_parameter(f, num, a, b):
# 计算定义域范围内的x坐标和y坐标的值
t = np.linspace(a, b, num)
x, y = f(t)
# 创建点
points = [gmsh.model.occ.addPoint(x[i], y[i], 0) for i in range(len(x))]
# 将点按顺序依次连接,创建线(形成闭合图形)
lines = [gmsh.model.occ.addLine(points[i], points[i + 1]) for i in range(len(points) - 1)]
# 创建线环
cloop = gmsh.model.occ.addCurveLoop(lines)
# 创建面
face = gmsh.model.occ.addPlaneSurface([cloop])
return face
测试文件代码:
import gmsh
import gmsh_occ_tools as tools
import math
import numpy as np
gmsh.initialize()
gmsh.model.add("model9")
# 定义域
a = 0
b = 2 * math.pi
# 均匀间隔点的个数
num = 100
# 参数方程的返回形式为x, y
def f(t):
k = 5
x = (2 + np.cos(k * t)) * np.cos(t)
y = (2 + np.cos(k * t)) * np.sin(t)
return x, y
# def f(t):
# x = 16 * np.sin(t)**3
# y = 13 * np.cos(t) - 5 * np.cos(2 * t)
# - 2 * np.cos(3 * t) - np.cos(4 * t)
# return x, y
# 由给定的参数方程生成网格 (f为参数方程函数, a, b 为参数域边界)
model3 = tools.model_made_parameter(f, num, a, b)
gmsh.model.occ.synchronize() # 同步
gmsh.model.mesh.generate(2) # 生成网格
gmsh.fltk.run() # 图形界面显示
gmsh.finalize() # 关闭gmsh
上述代码中,我们定义了两个参数方程,其中一个是花瓣曲线,参数k是花瓣的瓣数,另一个是生成一个爱心的曲线,之后调用要测试的函数: model_made_parameter,通过给定参数方程来生成网格。
效果如下:
注意,在调用我上面写的工具函数生成二维网格的过程中,不管是顶点还是极坐标还是参数方程,所给的点(按次序)以及定义域构成的二维图形必须是首位相连的封闭图形,否则将可能无法正常生成二维图形且报错。
以顶点坐标为参数的API(三维)
# p: 三维顶点坐标组成的列表
# pindex: 生成面的顶点索引的二维列表
def model_made_points(p, pindex):
# 创建点
points = [gmsh.model.occ.addPoint(*pt, lc) for pt in p]
# 创建边
lines = [[gmsh.model.occ.addLine(points[pindex[i][j-1]], points[pindex[i][j]]) for j in range(len(pindex[i]))]
for i in range(len(pindex))]
# 创建线环
cloops = [gmsh.model.occ.addCurveLoop(lines[i]) for i in range(len(lines))]
# 创建面
faces = [gmsh.model.occ.addPlaneSurface([cloops[i]]) for i in range(len(cloops))]
# 创建面环
surface_loop = gmsh.model.occ.addSurfaceLoop(faces)
# 创建体
volume = gmsh.model.occ.addVolume([surface_loop])
return volume
在上述函数中,需要提供两个二维列表,第一个顶点列表,形式和二维的一样,只是增加了一个维度,第二个是面列表。
面和顶点列表:使用顶点的坐标列表来定义多面体的各个顶点,并使用面的顶点索引列表来定义多面体的各个面。(正多面体的表达方式)。具体例子如下(vertices:顶点列表,faces:面列表)
测试文件代码:
import gmsh
import gmsh_occ_tools as tools
gmsh.initialize()
gmsh.model.add("model10")
# 顶点坐标
vertices = [
[0, 0, 0], # 0
[1, 0, 0], # 1
[1, 1, 0], # 2
[0, 1, 0], # 3
[0, 0, 1], # 4
[1, 0, 1], # 5
[1, 1, 1], # 6
[0, 1, 1] # 7
]
# 面坐标
faces = [
[0, 1, 2, 3], # 面1
[1, 5, 6, 2], # 面2
[5, 4, 7, 6], # 面3
[4, 0, 3, 7], # 面4
[3, 2, 6, 7], # 面5
[1, 0, 4, 5] # 面6
]
tools.model_made_points(vertices, faces)
gmsh.model.occ.addSurfaceLoop([1, 2, 3, 4, 5, 6])
# 创建体
gmsh.model.occ.addVolume([1])
gmsh.model.occ.synchronize()
gmsh.model.mesh.generate(2)
gmsh.fltk.run()
gmsh.finalize()
上述代码中,我们定义了一个正方体顶点列表和面列表,之后调用要测试的函数:model_made_points,通过给顶点坐标来生成三维正方体的面网格。
效果如下:
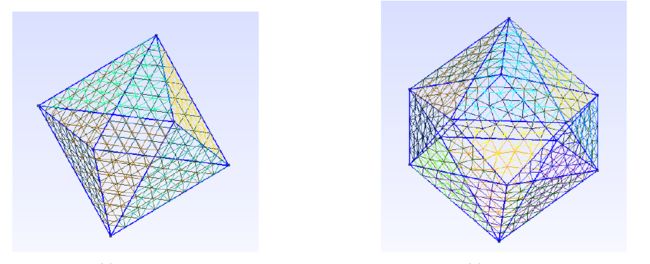
当然,我们还可以更换顶点坐标和面坐标来生成更复杂的多面体的面网格:
# 正八面体的顶点坐标和面坐标
vertices = [
[1, 0, 0], [-1, 0, 0], [0, 1, 0], [0, -1, 0], [0, 0, 1], [0, 0, -1]
]
faces = [
[0, 2, 4], [0, 4, 3], [0, 3, 5], [0, 5, 2], [1, 2, 5], [1, 5, 3],
[1, 3, 4], [1, 4, 2]
]
# 正十二面体的顶点坐标和面坐标
vertices = [
[0, 0, 1.225], [1.051, 0, 0.325], [0.324, 1.0, 0.325],
[-0.849, 0.618, 0.325], [-0.849, -0.618, 0.325], [0.324, -1.0, 0.325],
[0.849, 0.618, -0.325], [-0.324, 1.0, -0.325], [-1.051, 0, -0.325],
[-0.324, -1.0, -0.325], [0.849, -0.618, -0.325], [0, 0, -1.225]
]
faces = [
[0, 1, 2], [0, 2, 3], [0, 3, 4], [0, 4, 5], [0, 5, 1], [1, 6, 2],
[2, 7, 3], [3, 8, 4], [4, 9, 5], [5, 10, 1], [6, 7, 2], [7, 8, 3],
[8, 9, 4], [9, 10, 5], [10, 6, 1], [11, 6, 7], [11, 7, 8],
[11, 8, 9], [11, 9, 10], [11, 10, 6]
]
效果如下:
以球坐标方程为参数的API
# 用球坐标生成网格
# h: 球坐标方程函数
# a, b: theta的左右边界(默认为[0, 2*pi])
# c, d: phi的左右边界(默认为[0, pi])
# num: 均匀间隔点的个数
def model_made_globe(h, num, a=0, b=2 * math.pi, c=0, d=math.pi):
# 计算定义域范围内的x坐标、y坐标和z坐标的值
multiplier = num
theta = np.linspace(a, b, num)
phi = np.linspace(c, d, num)
r = h(theta, phi)
op = r * np.sin(phi)
x = [np.cos(a) * b for a in theta for b in op]
y = [np.sin(a) * b for a in theta for b in op]
temp = r * np.cos(phi)
z = []
for _ in range(multiplier):
z.extend(temp)
# 创建点
points = [gmsh.model.occ.addPoint(x[i], y[i], z[i]) for i in range(len(x))]
# 将点按顺序依次连接,创建线
lines1 = [gmsh.model.occ.addLine(points[num * i + j], points[num * i + j + 1])
for i in range(len(theta)) for j in range(len(phi) - 1)]
lines2 = [gmsh.model.occ.addLine(points[num * i + j], points[num * (i + 1) + j])
for j in range(1, len(theta) - 1) for i in range(len(phi) - 1)]
# 创建线环
cloops1 = [gmsh.model.occ.addCurveLoop([lines1[(num - 1) * i + j], -lines1[(num - 1) * (i + 1) + j],
lines2[i]]) for j in [0] for i in range(num - 1)]
cloops2 = [gmsh.model.occ.addCurveLoop([-lines1[(num - 1) * i + j], lines1[(num - 1) * (i + 1) + j],
lines2[i + (num - 1) * (num - 3)]]) for j in [num - 2] for i in range(num - 1)]
cloops3 = [gmsh.model.occ.addCurveLoop([lines1[i + j * (num - 1)], -lines2[(i - 1) * (num - 1) + j + (num - 1)],
-lines1[i + (j + 1) * (num - 1)], lines2[(i - 1) * (num - 1) + j]])
for i in range(1, num - 2) for j in range(num - 1)]
# 创建面
cloops = cloops1 + cloops3 + cloops2
face = [gmsh.model.occ.addPlaneSurface([cloops[i]]) for i in range(len(cloops))]
# 创建面环
surface_loop = gmsh.model.occ.addSurfaceLoop(face)
# 创建体
volume = gmsh.model.occ.addVolume([surface_loop])
return volume
测试文件代码:
import gmsh
import numpy as np
import gmsh_occ_tools as tools
# 均匀间隔点的个数
num = 100
# 定义球坐标 g(x) = 2 返回形式为极长(点到极点的距离)的值
def g(x, y):
rho = 2
return rho
# # 定义球坐标 g(x) = 0.2 + 0.05 * (1/8 * (35 * cos(x)^4-30 * cos(x)^2 + 3))
# def g(x, y):
# rho = 0.2 + 0.05 * (1/8 * (35 * np.cos(x)**4 - 30 * np.cos(x)**2 + 3))
# return rho
gmsh.initialize()
tools.model_made_globe(g, num)
gmsh.model.occ.synchronize()
gmsh.model.mesh.generate(2)
gmsh.fltk.run()
gmsh.finalize()
上述代码中,我们定义了两个球坐标,其中第一个是球,另一个是生成一个复杂的三维几何图形,之后调用要测试的函数:model_made_globe,通过给定球坐标方程来生成三维曲面图形的面网格。
效果如下:
注意,上述API皆为occ构建的,我还提供了由geo构建的完全相同的API(只需将occ改为geo即可)