Vivado时序分析

时序分析的基本方法

策略

• 基于路径的分析策略，在时序图中找到从起点和终点的所有路径并进行计算。
• 基于模块的分析策略，在时序图中中只侧重分析该路径下延迟最严重的节点进行计算

延时计算方法

• 组合逻辑
  • 任意时刻的输出只取决于输入，与电路的原来状态无关，但是实际在电路中延时计算需要指导输入上拉和下拉的延时。
• 时序逻辑
  • 任意时刻的输出取决于输入和原来的电路状态，但是时序逻辑仅在时钟有效沿工作，分别需要计算数据和时钟的路径延时

时序路径分析方法

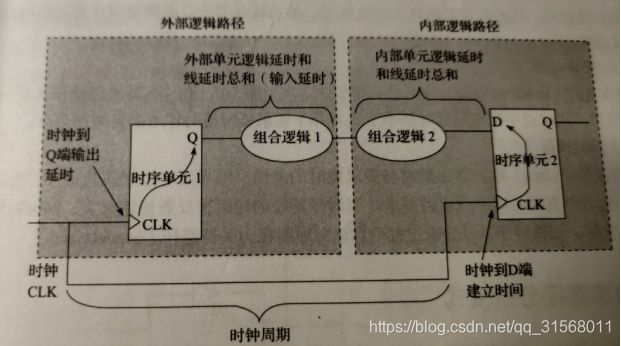
触发器到触发器

setup

$$\begin{gathered} cl{k}_{launch}+FF{1}_{CLK->Q}+Logic⩽ \\ cl{k}_{capture}+cl{k}_{period}-FF{2}_{setup} \end{gathered}$$

hold

$$\begin{gathered} cl{k}_{launch}+FF{1}_{CLK->Q}+Logic⩾ \\ cl{k}_{capture}+FF{2}_{hold} \end{gathered}$$

输入端到触发器

输入端到触发器的模型类似于触发器到触发器的模型，只需要将外部模型当作FF1就可以了，该路径的发射时延通过设置虚拟时钟来实现。

setup

$$\begin{gathered} virtualcl{k}_{launch}+FF{1}_{CLK->Q}+Logic1+Logic2⩽ \\ cl{k}_{capture}+cl{k}_{period}-FF{2}_{setup} \end{gathered}$$

hold

$$\begin{gathered} virtualcl{k}_{launch}+Inpu{t}_{dealay}+Logic2⩾ \\ cl{k}_{capture}+FF{2}_{hold} \end{gathered}$$

触发器到输出端

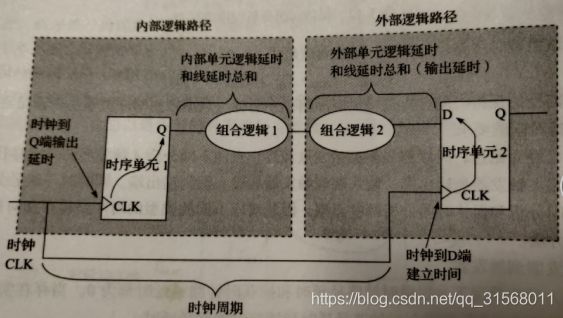
触发器到输出端模型同样类似于触发器到触发器的模型，只需要将外部模型当作FF2就可以了，该捕获的发射时延也通过设置虚拟时钟来实现

setup

$$\begin{gathered} cl{k}_{launch}+FF{1}_{CLK->Q}+Logic1+Logic2⩽ \\ virtualcl{k}_{capture}+cl{k}_{period}-FF{2}_{setup} \end{gathered}$$

hold

$$\begin{gathered} cl{k}_{launch}+FF{1}_{CLK->Q}+Logic1+Logic2⩾ \\ virtualcl{k}_{capture}+FF{2}_{hold} \end{gathered}$$

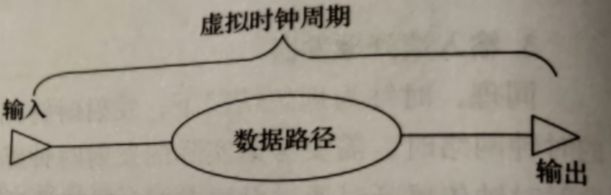
输入到输出端

step

$$Logic⩽virtua{l}_{period}-Input-Output$$

hold

$$Logic⩾F{F}_{hold}-Input-Output$$

分析模式

• 最快路径：信号传输延时计算调用最快工艺参数的路径
• 最慢路径：信号传输延时计算调用最慢工艺参数的路径

单一分析

• 最好的：较小的工艺偏差、较低的工作温度、较高的工作电压
• 最坏的：较大的工艺偏差、较高的工作温度、较低工作电压
• 典型位于两者之间

单一静态时序分析将指定其中一种工作条件下检查建立时间和保持时间

最坏最好分析

将在最好和最坏下进行分析和单一分析的计算方式一样，不同在于所使用的延时时序库的参数不同，计算建立用最大的延时库，计算保持用最小延时库

OCV

和前面的计算方法一样，不同在于计算最快和最慢路径有差别，最慢路径下调用最大延时，最快路径下调用最短延时。快慢的路径得出依赖于逻辑深度和逻辑单元的延时

例子1：vivado约束

以下面的例子介绍不同的约束手段

module time_practice(
input  clk,
input  sa,
output reg sb
    );
    
    always @(posedge clk)begin
        if(sa)
        sb <= 1'b1;
        else
        sb <= 1'b0;
    end
    
endmodule

芯片时xc7a35t实际上芯片在这里不重要

create_clock -period 20.000 -name sys_clk -waveform {0.000 10.000} [get_ports clk]

set_property PACKAGE_PIN R2 [get_ports sa]
set_property IOSTANDARD LVCMOS33 [get_ports sa]

set_property PACKAGE_PIN R3 [get_ports sb]
set_property IOSTANDARD LVCMOS33 [get_ports sb]

set_input_delay -clock sys_clk -max 1.0 [get_ports sa]
set_input_delay -clock sys_clk -min 0.5 [get_ports sa]

set_output_delay -clock sys_clk -max 1.0 [get_ports sb]
set_output_delay -clock sys_clk -min 0.5 [get_ports sb]

综合后的图，vivado自动给我们添加IBUF BUFG 和OBUF

sa->sb_reg建立时间

vivado分析信号sa到触发器的D的建立时间路径如下：

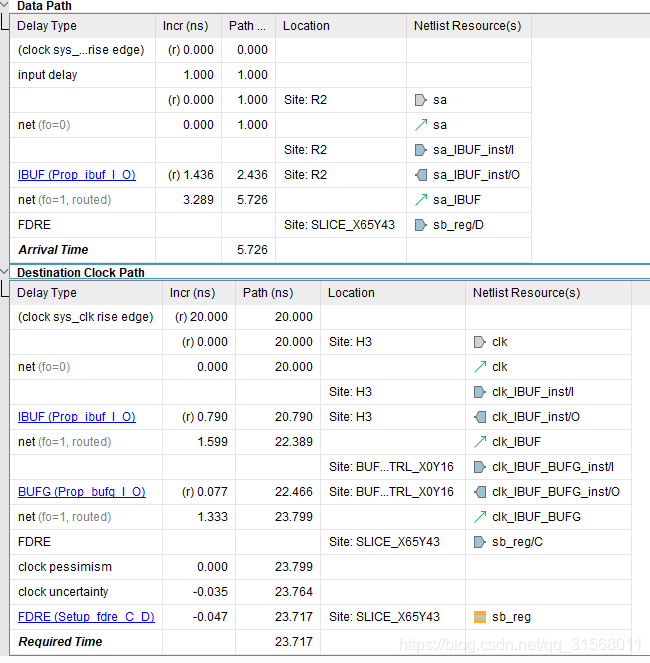
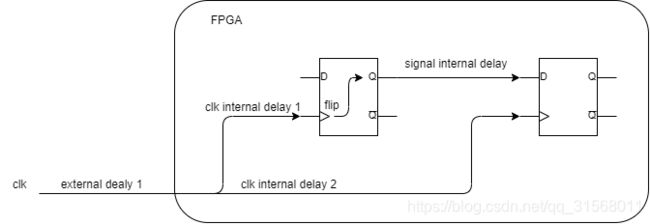
实际时序分析的模型是从输入的到触发器，其中建立公式

$$\begin{gathered} cl{k}_{lauch}=cl{k}_{external\_1}+ex{1}_{delay} \\ cl{k}_{capture}=cl{k}_{external\_2}+cl{k}_{internal\_delay} \\ cl{k}_{lauch}+ex{2}_{delay}+ex{3}_{delay}+ex{4}_{delay}+signa{l}_{internal\_delay}⩽cl{k}_{capture}+CL{K}_{period}-D_{setup} \end{gathered}$$
在vivado中分析认为
$$\begin{gathered} ex{1}_{delay}+ex{2}_{delay}+ex{3}_{delay}++ex{4}_{delay}=input\_dealy \\ cl{k}_{external\_1}=cl{k}_{external\_2} \end{gathered}$$

化简后
$$input\_dealy+signa{l}_{internal\_delay}⩽cl{k}_{internal\_delay}+CL{K}_{period}-D_{setup}$$
vivado从极端的条件下考虑，总是将等式左边的等式的变化量取极大值，右边的等式变化量取极小值。

Data Path

将sa信号的套入上面的式子
$$\begin{array}{rl}input\_dealy& =1\\ signa{l}_{internal\_delay}& =1.436(IBUF)+3.289(net)\\ input\_dealy+signa{l}_{internal\_delay}& =5.726\end{array}$$
$input\_dealy$ 在这里是1，因为有约束sa信号最大的输入延时是1，若以最大的延时计算都能满足等式，自然其他时候也能够满足条件。

Clock Path

$$\begin{array}{rl}cl{k}_{internal\_delay}& =0.79(IBUF)+1.599(net)+0.077(BUFG)+1.333(net)\\ CL{K}_{period}& =20\\ D_{setup}& =0.047\\ cl{k}_{uncertainty}& =0.035\\ cl{k}_{internal\_delay}+CL{K}_{period}-D_{setup}-cl{k}_{uncertainty}& =23.717\end{array}$$

在vivado分析种还有clock pessimism （时序悲观，存在于有共同路径上，没有所以0）和 clock uncertainty（时序不确定性，在极端条件要影响这个等式不满足只能把它往左边的等式加，因为在将它往左边等式加的过程中如果依然满足等式条件，那么没有它存在自然也满足）。
$$slack=ClockPath-DataPah=17.991$$

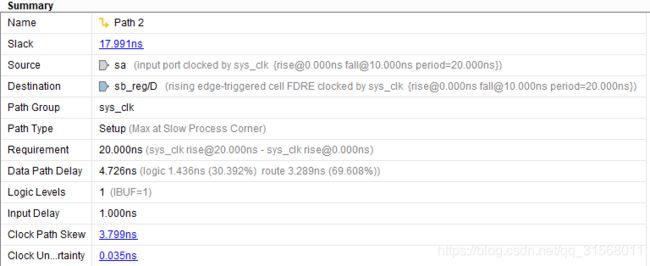
可以看到分析建立时间的路径采用最慢路径的最大时延工艺参数。

sa->sb_reg保持时间

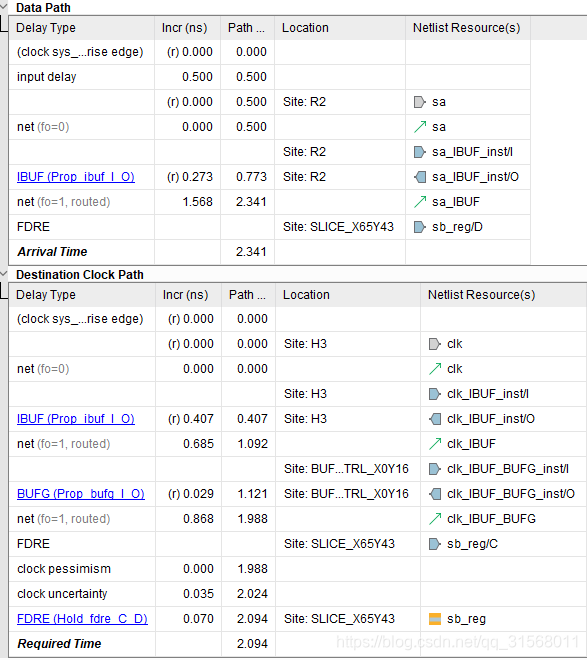
其中保持时间公式
$$\begin{gathered} cl{k}_{lauch}=cl{k}_{external\_1}+ex{1}_{delay} \\ cl{k}_{capture}=cl{k}_{external\_2}+cl{k}_{internal\_delay} \\ cl{k}_{lauch}+ex{2}_{delay}+ex{3}_{delay}+ex{4}_{delay}+signa{l}_{internal\_delay}⩾cl{k}_{capture}+D_{hold} \end{gathered}$$
化简
$$input\_dealy+signa{l}_{internal\_delay}⩾cl{k}_{internal\_delay}+D_{hold}$$

vivado从极端的条件下考虑，总是将等式左边的等式的变化量取极小值，右边的等式变化量取极大值。

Data Path

$$\begin{array}{rl}input\_dealy& =0.5\\ signa{l}_{internal\_delay}& =0.273(IBUF)+1.568(net)\\ input\_dealy+signa{l}_{internal\_delay}& =2.341\end{array}$$

$input\_dealy$ 在这里是0.5，因为有约束sa信号最小的输入延时是0.5，若以最小的延时计算都能满足等式，自然其他时候也能够满足条件。

Clock Path

$$\begin{array}{rl}cl{k}_{internal}& =0.407(IBUF)+0.685(net)+0.029(BUFG)+0.868(net)\\ D_{hold}& =0.070\\ cl{k}_{uncertainty}& =0.035\\ cl{k}_{internal}+D_{hold}+cl{k}_{uncertainty}& =2.094\end{array}$$

同样在vivado分析种还有clock pessimism （时序悲观，存在于有共同路径上，没有所以0）和 clock uncertainty（时序不确定性，时序不确定性，在极端条件要影响这个等式不满足只能把它往右边的等式加，因为在将它往右边等式加的过程中如果依然满足等式条件，那么没有它存在自然也满足）。
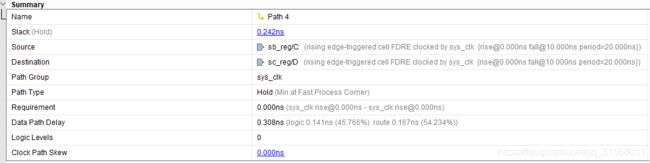
$$slack=DataPah-ClockPath=0.248$$

可以看到分析保持的路径采用最快路径的最小时延工艺参数。
这也就解释了为什么在$cl{k}_{internal}$一样的路径下得到的延时参数不一致。

sb_reg->sb建立时间

vivado分析触发器sb到输出端口的建立时间路径如下：

实际时序分析的模型是从触发器到输出端，其中建立公式

$$\begin{gathered} cl{k}_{lauch}=cl{k}_{external\_1}+cl{k}_{internal\_delay} \\ cl{k}_{capture}=cl{k}_{external\_2}+ex{3}_{delay} \\ cl{k}_{lauch}+fli{p}_{delay}+signa{l}_{internal\_delay}+ex{1}_{delay}+ex{2}_{delay}⩽cl{k}_{capture}+CL{K}_{period}-D_{setup} \end{gathered}$$
在vivado中分析认为
$$\begin{gathered} ex{1}_{delay}+ex{2}_{delay}+D_{setup}-ex{3}_{delay}=output\_dealy \\ cl{k}_{external\_1}=cl{k}_{external\_2} \end{gathered}$$
化简后
$$cl{k}_{internal\_delay}+fli{p}_{delay}++signa{l}_{internal}⩽CL{K}_{period}-outpu{t}_{d}elay$$
vivado从极端的条件下考虑，总是将等式左边的等式的变化量取极小值，右边的等式变化量取极大值。

Data Path

$$\begin{array}{rl}cl{k}_{internal\_delay}& =0.921(IBUF)+1.689(net)+0.081(BUFG)+1.443(net)\\ flip\_dealy& =0.379(FDRE)\\ signa{l}_{internal\_delay}& =1.385(net)+3.309(OBUF)\\ cl{k}_{internal\_delay}+flip\_dealy+signa{l}_{internal\_delay}& =9.206\end{array}$$

Clock Path

$$\begin{array}{rl}CL{K}_{period}& =20\\ cl{k}_{uncertainty}& =0.035\\ outpu{t}_{delay}& =1\\ CL{K}_{period}-outpu{t}_{delay}-cl{k}_{uncertainty}& =18.965\end{array}$$

$outpu{t}_{delay}$在这里是1，因为有约束sb信号最大的输出延时是1，若以最大的输出延时计算都能满足等式，自然其他时候也能够满足条件。

在vivado分析种还有clock pessimism （时序悲观，存在于有共同路径上，没有所以0）和 clock uncertainty（时序不确定性，在极端条件要影响这个等式不满足只能把它往左边的等式加，因为在将它往左边等式加的过程中如果依然满足等式条件，那么没有它存在自然也满足）。

可以看到分析建立时间的路径采用最慢路径的最大时延工艺参数。

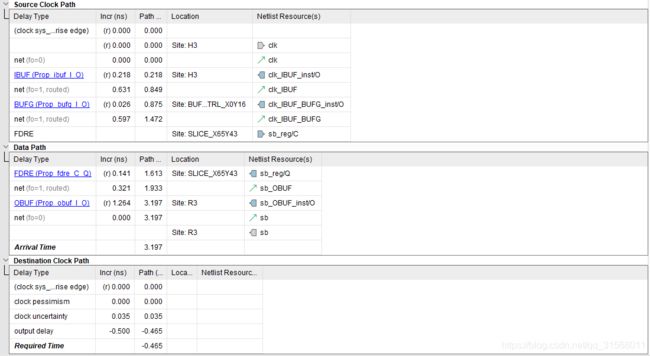
sb_reg->保持时间

其中保持时间公式
$$\begin{gathered} cl{k}_{lauch}=cl{k}_{external\_1}+cl{k}_{internal\_delay} \\ cl{k}_{capture}=cl{k}_{external\_2}+ex{3}_{delay} \\ cl{k}_{lauch}+fli{p}_{delay}+signa{l}_{internal\_delay}+ex{1}_{delay}+ex{2}_{delay}⩾cl{k}_{capture}+D_{hold} \end{gathered}$$
在vivado中分析认为
$$\begin{gathered} ex{1}_{delay}+ex{2}_{delay}-D_{hold}-ex{3}_{delay}=output\_dealy \\ cl{k}_{external\_1}=cl{k}_{external\_2} \end{gathered}$$
化简后
$$cl{k}_{internal\_delay}+fli{p}_{delay}++signa{l}_{internal}⩾-outpu{t}_{delay}$$
vivado从极端的条件下考虑，总是将等式左边的等式的变化量取极小值，右边的等式变化量取极大值。

Data Path

$$\begin{array}{rl}cl{k}_{internal\_delay}& =0.218(IBUF)+0.631(net)+0.026(BUFG)+0.597(net)\\ fli{p}_{delay}& =0.141(FDRE)\\ signa{l}_{internal\_delay}& =0.321(net)+1.264(OBUF)\\ cl{k}_{internal\_delay}+fli{p}_{delay}+signa{l}_{internal\_delay}& =3.197\end{array}$$

Clock Path

$$\begin{array}{rl}cl{k}_{uncertainty}& =0.035\\ outpu{t}_{delay}& =0.5\\ cl{k}_{uncertainty}-outpu{t}_{delay}& =-0.465\end{array}$$

$outpu{t}_{delay}$在这里是0.5，因为有约束sb信号最小的输出延时是0.5，若以最小的输出延时计算都能满足等式，自然其他时候也能够满足条件。

同样在vivado分析中还有clock pessimism （时序悲观，存在于有共同路径上，没有所以0）和 clock uncertainty（时序不确定性，在极端条件要影响这个等式不满足只能把它往右边的等式加，因为在将它往右边等式加的过程中如果依然满足等式条件，那么没有它存在自然也满足）。

可以看到分析保持时间的路径采用最快路径的最小时延工艺参数。

因此按照分析原则，vivado默认的静态时序分析模式是OCV

例子2：vivado约束

module time_practice(
input  clk,
input sa,
output reg sc
    );
    reg sb;   
    always @(posedge clk)begin
        if(sa)
        sb <= 1'b1;
        else
        sb <= 1'b0;
    end
        always @(posedge clk)begin
            sc<=sb;
    end
endmodule

芯片时xc7a35t实际上芯片在这里不重要

create_clock -period 20.000 -name sys_clk -waveform {0.000 10.000} [get_ports clk]

set_property PACKAGE_PIN R2 [get_ports sa]
set_property IOSTANDARD LVCMOS33 [get_ports sa]

set_property PACKAGE_PIN R3 [get_ports sc]
set_property IOSTANDARD LVCMOS33 [get_ports sc]

set_input_delay -clock sys_clk -max 1.0 [get_ports sa]
set_input_delay -clock sys_clk -min 0.5 [get_ports sa]

set_output_delay -clock sys_clk -max 1.0 [get_ports sc]
set_output_delay -clock sys_clk -min 0.5 [get_ports sc]

综合后的图，vivado自动给我们添加IBUF BUFG 和OBUF,不过这里分析sb到sc的信号

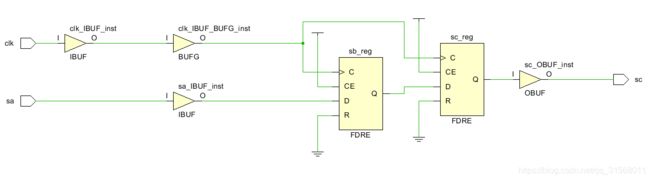
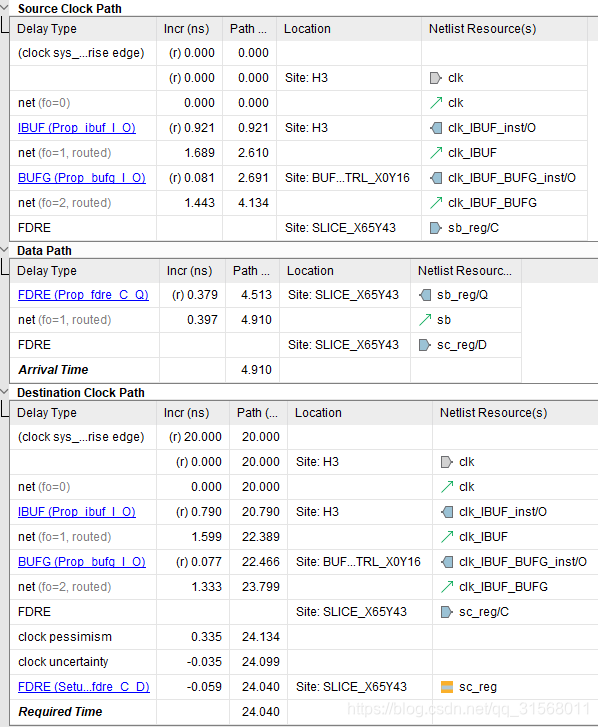
sb_reg->sc_reg建立时间

vivado分析信号sb到sc的D的建立时间路径如下：

实际时序分析的模型是从触发器到触发器

其中建立公式

$$\begin{gathered} cl{k}_{lauch}=cl{k}_{external\_1}+cl{k}_{internal\_delay\_1} \\ cl{k}_{capture}=cl{k}_{external\_1}+cl{k}_{internal\_delay\_2} \\ cl{k}_{lauch}+fli{g}_{delay}+signa{l}_{internal\_delay}⩽cl{k}_{capture}+CL{K}_{period}-D_{setup} \end{gathered}$$
化简
$$cl{k}_{internal\_delay\_1}+fli{p}_{delay}+signa{l}_{internal\_delay}⩽cl{k}_{internal\_delay\_2}+CL{K}_{period}-D_{setup}$$
vivado从极端的条件下考虑，总是将等式左边的等式的变化量取极大值，右边的等式变化量取极小值。

Data Path

$$\begin{array}{rl}cl{k}_{internal\_delay\_1}& =0.921(IBUF)+1.689(net)+0.081(BUFG)+(1.443)net\\ fli{p}_{delay}& =0.379(FDRE)\\ signa{l}_{internal\_delay}& =0.397(net)\\ cl{k}_{internal\_delay\_1}+fli{p}_{delay}+signa{l}_{internal\_delay}& =4.910\end{array}$$

Clock Path

$$\begin{array}{rl}cl{k}_{internal\_delay\_2}& =0.79(IBUF)+1.599(net)+0.077(BUFG)+(1.333)net\\ CL{K}_{period}& =20\\ D_{setup}& =0.059(net)\\ cloc{k}_{pessimism}& =0.335\\ cloc{k}_{uncertainty}& =0.035\\ cl{k}_{internal\_delay\_2}+CL{K}_{period}-D_{setup}+cloc{k}_{pessimism}-cloc{k}_{uncertainty}& =24.040\end{array}$$

• clock pessimism

  • 时序悲观，可以看到到sb_reg和sc_reg的时钟路径上其实是同一路径也就是说$cl{k}_{internal\_delay\_1}$和$cl{k}_{internal\_delay\_2}$在综合图上路径是一致的，因此实际上延迟是一致的，不应该为了极端方式在路径上$cl{k}_{internal\_delay\_1}$使用最慢路径，在路径上$cl{k}_{internal\_delay\_2}$使用最快路径。为了补偿他们的差值

$$cloc{k}_{pessimism}=cl{k}_{internal\_delay\_1}-cl{k}_{internal\_delay\_2}=0.335$$

• clock uncertainty
  • 时序不确定性，在极端条件要影响这个等式不满足只能把它往左边的等式加，因为在将它往左边等式加的过程中如果依然满足等式条件，那么没有它存在自然也满足。

$$slack=ClockPath-DataPath=19.130$$

分析建立时间使用了最慢路径的最大延时工艺参数

sb_reg->sc_reg保持时间

vivado分析信号sb到sc的D的保持时间路径如下：

其中保持公式

$$\begin{gathered} cl{k}_{lauch}=cl{k}_{external\_1}+cl{k}_{internal\_delay\_1} \\ cl{k}_{capture}=cl{k}_{external\_1}+cl{k}_{internal\_delay\_2} \\ cl{k}_{lauch}+fli{g}_{delay}+signa{l}_{internal\_delay}⩾cl{k}_{capture}+D_{hold} \end{gathered}$$
化简
$$cl{k}_{internal\_delay\_1}+fli{p}_{delay}+signa{l}_{internal\_delay}⩾cl{k}_{internal\_delay\_2}+D_{hold}$$

Data Path

$$\begin{array}{rl}cl{k}_{internal\_delay\_1}& =0.218(IBUF)+0.631(net)+0.026(BUFG)+(0.597)net\\ fli{p}_{delay}& =0.141(FDRE)\\ signa{l}_{internal\_delay}& =0.167(net)\\ cl{k}_{internal\_delay\_1}+fli{p}_{delay}+signa{l}_{internal\_delay}& =1.780\end{array}$$

Clock Path

$$\begin{array}{rl}cl{k}_{internal\_delay\_2}& =0.407(IBUF)+0.685(net)+0.029(BUFG)+(0.868)net\\ D_{hold}& =0.066(net)\\ cloc{k}_{pessimism}& =-0.517\\ cl{k}_{internal\_delay\_2}+D_{hold}+cloc{k}_{pessimism}& =24.040\end{array}$$

clock pessimism

• 时序悲观，可以看到到sb_reg和sc_reg的时钟路径上其实是同一路径也就是说$cl{k}_{internal\_delay\_1}$和$cl{k}_{internal\_delay\_2}$在综合图上路径是一致的，因此实际上延迟是一致的，不应该为了极端方式在路径上$cl{k}_{internal\_delay\_1}$使用最快路径，在路径上$cl{k}_{internal\_delay\_2}$使用最慢路径。为了补偿他们的差值

$$cloc{k}_{pessimism}=cl{k}_{internal\_delay\_1}-cl{k}_{internal\_delay\_2}=-0.517$$

$$slack=ClockPath-DataPath=19.130$$

但是这里突然没有$cloc{k}_{uncertainty}$感觉有些奇怪。

$$\begin{array}{rl}cl{k}_{internal\_delay\_2}& =0.407(IBUF)+0.685(net)+0.029(BUFG)+(0.868)net\\ D_{hold}& =0.066(net)\\ cloc{k}_{pessimism}& =-0.517\\ cl{k}_{internal\_delay\_2}+D_{hold}+cloc{k}_{pessimism}& =24.040\end{array}$$

clock pessimism

• 时序悲观，可以看到到sb_reg和sc_reg的时钟路径上其实是同一路径也就是说$cl{k}_{internal\_delay\_1}$和$cl{k}_{internal\_delay\_2}$在综合图上路径是一致的，因此实际上延迟是一致的，不应该为了极端方式在路径上$cl{k}_{internal\_delay\_1}$使用最快路径，在路径上$cl{k}_{internal\_delay\_2}$使用最慢路径。为了补偿他们的差值

$$cloc{k}_{pessimism}=cl{k}_{internal\_delay\_1}-cl{k}_{internal\_delay\_2}=-0.517$$

$$slack=ClockPath-DataPath=19.130$$

但是这里突然没有$cloc{k}_{uncertainty}$感觉有些奇怪。

分析建立时间使用了最快路径的最小延时工艺参数。