数据结构之插入排序

目录

前言

插入排序

直接插入排序

插入排序的时间复杂度

希尔排序 

---

前言

在日常生活中，我们不经意间会遇到很多排序的场景，比如在某宝，某东上买东西，我们可以自己自定义价格是由高到低还是由低到高，再比如在王者某耀中的每个英雄的荣耀战力，都是由高到低进行排序的，这些场景都用到了排序，但是这些场景的底层都是用一个个排序算法来实现的，本期开始，我们就要学习数据结构中很重要的一个知识点-------排序。

 几种常见的排序：

注：我们今后所有的排序都默认排升序。

本期我们主要讲解插入排序。

插入排序

直接插入排序

直接插入排序在现实生活中最常见的应用其实就是斗地主时，我们一般会将牌拍好序，然后根据自己的打法打牌，大家先仔细想想，再给牌整理时我们是怎样整理的呢？当我们摸到第一张牌时，此时它已经有序，我们摸第二张牌时，就会与第一张牌做比较，然后发生交换使之成为我们想要的顺序，当我们摸第三张牌时，我们又会与最后一张牌与倒数第二张牌进行比较，交换之后使牌的顺序成为我们想要的顺序，之后每摸一张牌，就按照此方法进行整理，最后就会得到一个有序的牌列。这就直接插入排序的一个比较常见的应用场景。在数据结构中，我们怎样实现直接插入排序呢？

要实现直接插入排序，我们可以先将直接插入排序分解为单趟排序，然后再让每趟排序组合成为整个排序。

单趟排序：

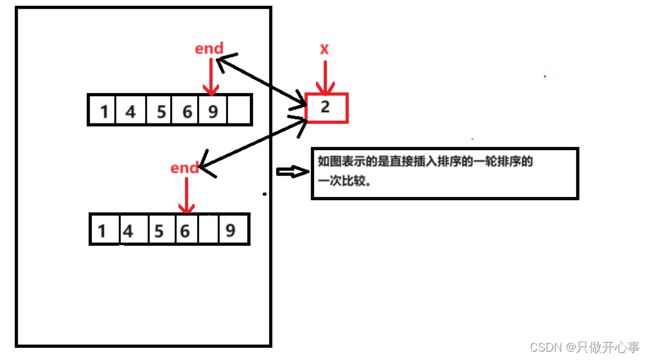
单趟排序的情景：我们要将一个元素插入一个有序数组之中。可以类比，我们摸了一张牌还没有插入手中的牌中，但是手中的牌肯定已经是一个有序的牌序列了。

单趟排序的算法思想：我们令有序的数组的最后一个元素的位置为end，要插入的元素为x。要将x插入一个有序数组，就得先让x与end位置上的元素进行比较，因为我们是排升序，所以如果x比a[end]小，就要把a[end]向后挪动一个位置，然后将end--，然后在让x与此时end位置上的元素a[end]进行比较，比较的原理同上，直到将x插入到合理的位置，那么怎样判断这样的一趟排序已经结束了呢？其实就是x比当前end位置上的元素要大，这是一个结束条件，还有就是x比有序数组所有的元素都要小，即就是要将x放在数组的第一个元素的位置上，此时end已经到了数组第一个元素位置的前一个位置之前，我们称此时end==-1，所以综上，一趟排序的结束标志就是x>a[end]或者end<0

单趟排序代码实现：

int end = size - 1;
	int x;
	while (end >= 0)
	{
		if (a[end] > x)
		{
			a[end + 1] = a[end];
			end--;
		}
		else 
		{
			break;
		}
	}
	a[end + 1] = x;

 到了这里，我们单趟排序已经搞定了，但是上面我们已经说了，我们把整个插入排序分为了每趟排序，那么怎样将每趟排序合并成为直接插入排序呢？

每趟排序的关键点在于是把一个元素插入一个有序数组之中，其实对于一个数组而言，无论它是否是有序还是无序的，其第一个元素毋庸置疑肯定是有序的，这便是关键，我们可以从第一个与元素开始，把第一个元素当成一个有序数组，此时第二个元素就是要插入有序数组中的元素，那么此时第二哥元素插入由第一个元素组成的有序数组中就可以看成是一趟排序，这趟排序之后，第一个元素和第二个元素就组成了一个有序数组，第三个元素插入由第一个和第二个元素组成的有序数组就可以看成第二趟排序，由此依次进行多趟排序，那么整个数组的多趟排序就最终组成了直接插入排序。

直接插入排序完整代码：

void InsertSort(int* a, int size)
{
	assert(a);
	for(int end=0;end= 0)
		{
			if (a[end] > x)
			{
				a[end + 1] = a[end];
				end--;
			}
			else
			{
				break;
			}
		}
		a[end + 1] = x;
	
	}
}
int main()
{
	int arr[] = { 10,9,8,7,6,5,4,3,2,1 };
	InsertSort(arr, sizeof(arr) / sizeof(int));
	for (int i = 0; i < sizeof(arr) / sizeof(int); i++)
	{
		printf("%d ", arr[i]);
	}
	return 0;

}

运行截图如下：

注意：

排序这里比较重要的就是边界的控制，对于直接插入排序而言，若数组的大小为size。end的初始值就是0，end的最终值就是size-2，x的初始位置就是1，x的最终位置就是size-1。

以上便是直接插入排序的整个过程。

插入排序的时间复杂度

最好：O(N),已经有序的数组，要插入的元素比end位置上的元素大，只用跟end位置上的元素比较一下。

最坏：O(N^2)，逆序，要插入的元素比有序数组的所有元素都要小，跟end位置和end位置之前的所有元素都要比较一下。

稳定性：稳定。

希尔排序 

希尔排序其实就是插入排序的进阶版，我们知道，一个数组越有序，直接插入排序的时间复杂度越低，希尔排序其实就是为了将一个无序的数组变得有序，使插入排序变得更加简单。

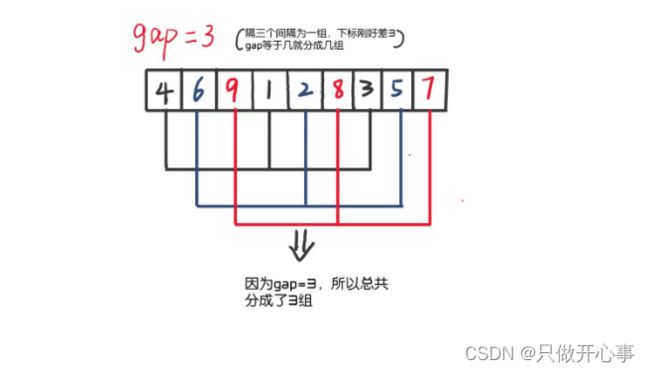
希尔排序如图：

希尔排序的思想：先设置一个gap值，先把整个数组的元素分成gap组，即下标差gap的为一组，然后对每一组按照直接插入排序的思想进行排序，每一组的排序将完成一次预排序，每完成一次预排序，数组会变得比之前更加有序。我们再改变gap的值多次进行预排序，当gap==1时，就是直接插入排序，此时因为经历了多次预排序，整个数组已经变得有序，所以此时再用直接插入排序对整个数组完成最终的排序。

希尔排序的整体代码：

void ShellSort(int* a, int size)
{
	int gap = size;
	while (gap > 1)
	{
		gap /= 2;
		//进行一趟预排序
		for (int i = 0; i < gap; i++)
		{
			//进行每组排序
			for (int end = i; end < size - gap; end += gap)
			{
				int x = a[end + gap];
				//进行单趟排序
				while (end >= 0)
				{
					if (a[end] > x)
					{
						a[end + gap] = a[end];
						end -= gap;
					}
					else
					{
						break;
					}
				}
				a[end + gap] = x;
			}
		}
	}
}
int main()
{
	int arr[] = { 10,9,2,8,6,5,4,3,11,1 };
	ShellSort(arr, sizeof(arr) / sizeof(int));
	for (int i = 0; i < sizeof(arr) / sizeof(int); i++)
	{
		printf("%d ", arr[i]);
	}
	return 0;
}

 运行截图如下：

当然，上述的方法是把三组的排序是分开的，每组自己排自己的，但是下面这种方法就是三种排序我们再一次排序中就全部排序完成，更为简洁，但是没有第一种好理解，可以理解为是第一种方法的进阶版本，但是这种进阶版本是我们经常使用的。

进阶版本代码如下：

void ShellSort(int* a, int size)
{
	int gap = size;
	while (gap > 1)
	{
		gap /= 2;
		//进行一趟预排序,将多组排序在一次排序中就完成了，而不是按组进行排序
			for (int end = 0; end < size - gap; end++)
			{
				int x = a[end + gap];
				//进行单趟排序
				while (end >= 0)
				{
					if (a[end] > x)
					{
						a[end + gap] = a[end];
						end -= gap;
					}
					else
					{
						break;
					}
				}
				a[end + gap] = x;
			}
	}
}
int main()
{
	int arr[] = { 10,19,2,8,6,0,4,3,11,1 };
	ShellSort(arr, sizeof(arr) / sizeof(int));
	for (int i = 0; i < sizeof(arr) / sizeof(int); i++)
	{
		printf("%d ", arr[i]);
	}
	return 0;
}

以上便是希尔排序的整个过程。

希尔排序的时间复杂度

 希尔排序的时间复杂度为：

1.最好：O(N),当整个数组为有序数组时，复杂度最小。排序算法的时间复杂度的天花板就是O(N)

 2.最坏：总共分成了gap组，每组大概就是size/gap个元素，如果每组都逆序，那么每组的复杂度又是一个1+2+...+size/gap的等差数列，平均是O(N^1.3)。

稳定性：不稳定。

插入排序的内容就是这些，我们需要注意的仍然是算法中边界的控制，在编写代码时，我们可以自己画图去控制边界，这是一个很好的方法。

好了，本期的内容到此结束^_^