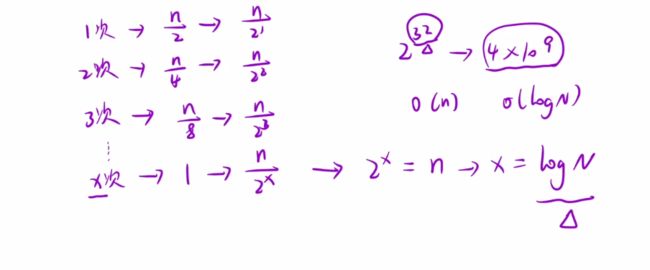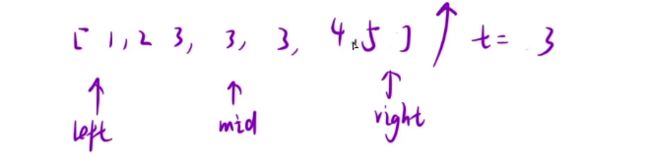算法——二分查找
二分算法简介：
- 二分查找算法只适用于数组有序的情况？（只要数组中存在某种规律就可以用）
- 模版：
- 朴素的二分模版
- 查找左边界的二分模版
- 查找右边界的二分模版
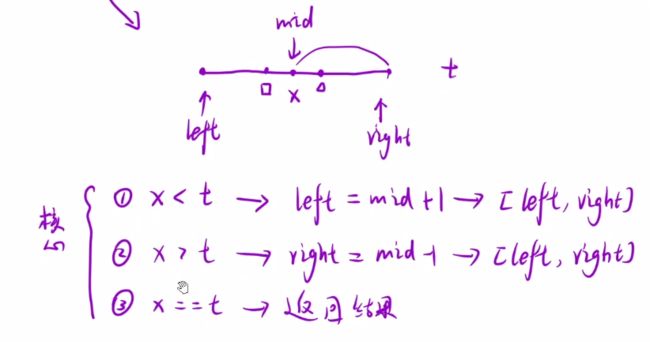
朴素二分模版
while(left <= right)
{
int mid = left+ (right-left+1)/2 ; //防止溢出
if(...)
left = mid+1;
else if(...)
right = mid-1;
else
return ...;
}
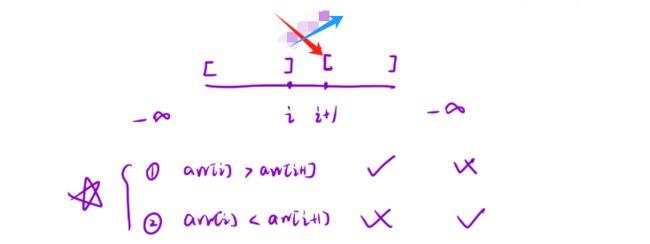
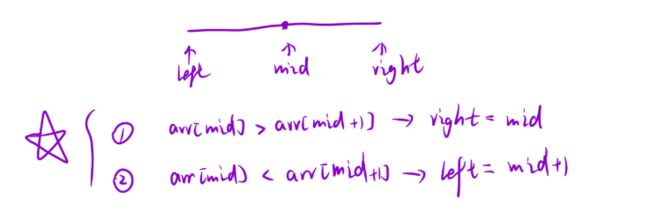
查找区间左端点/右端点的二分模版
二分查找
二分查找
题目解析
- n个元素有序的数组，找到 target并返回数组下标
算法原理
-
暴力解法：从头到尾遍历，若找到目标值返回下标，否则返回-1。时间复杂度O(n)，但并没有利用数组的有序性
-
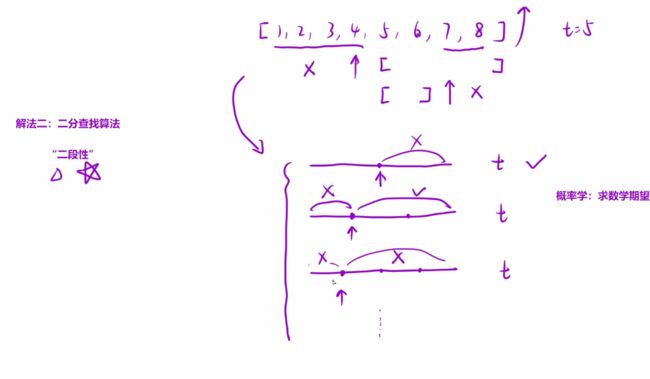
一个数组中，随机找一个数，去和target进行比较，做完比较之后，划分出两个区域；其中根据规律可以有选择性的舍去一个规律，继续在另一个规律中寻找。此时该题目具有二段性，我们可以用二分查找算法(这里选取二分之一是最优选择，因为他的时间复杂度以及根据概率学问题是最优的)
-
朴素二分查找算法：我们来探讨一下细节问题
-
循环结束的条件：left>right
-
为什么是正确的：因为我们是从暴力解法优化而来的，相较于法一的逐个淘汰，二分查找可以帮我们一次性淘汰一段区间的数字
-
时间复杂度：
代码实现
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0,right = nums.size()-1;
while(left <= right)
{
int mid = left+ (right-left)/2 ; //防止溢出
if(nums[mid] < target) left = mid+1;
else if(nums[mid] > target) right = mid-1;
else return mid;
}
return -1;
}
};
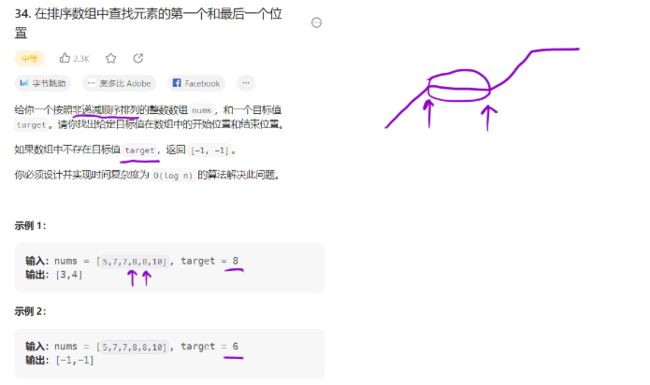
在排序数组中查找元素的第一个和最后一个位置
在排序数组中查找元素的第一个和最后一个位置
题目解析
- 该数组为非递减序列的数组，返回目标值开始和结束的位置。如果不存在返回-1（注：题中示例三，如果是空数组，为了避免造成越界访问，我们要特殊处理，直接返回-1）
算法原理
- 暴力解法：从前往后遍历数组一遍，此时时间复杂度O(n)。
- 朴素二分：虽然可以找到目标值，但是不确定该值是否是起始位置或者终点位置，可能还需要向前遍历和向后遍历寻找，所以极端情况下他的时间复杂度为O(n)
- 优化朴素二分
寻找左边界
-
寻找左边界：retLeft 表⽰左边界， retRight 表⽰右边界
我们注意到以左边界划分的两个区间的特点：- 左边区间[left, retLeft - 1] 都是⼩于 x 的；
- 右边区间（包括左边界） [retLeft, right] 都是⼤于等于 x 的；
-
因此，关于mid的落点，我们可以分为下⾯两种情况：
-
当我们的 mid 落在 [left, retLeft - 1] 区间的时候，也就是 arr[mid]
-
当mid落在 [retLeft， right] 的区间的时候，也就是 arr[mid] >= target 。说明 [mid + 1, right] （因为 mid 可能是最终结果，不能舍去）是可以舍去的，此时更新 right 到 mid 的位置，继续在 [left, mid] 上寻找左边界
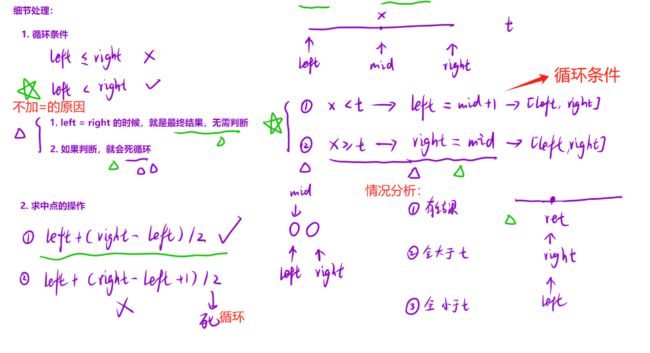
细节处理：
-
-
循环条件：这里要写成left
- 这里说一下会死循环的原因：当判断等号的情况时，right+left会进入第二个条件，但right位置不变，mid依旧是这个位置，下次进入判断循环条件时会继续进入第二个，此时进入死循环。
-
求中点操作：若用第二个，则mid会落在right的位置上，此时如果进入第一个循环条件没问题，但是进入第二个循环条件，right位置没有动，求出的mid还是这个位置，下次进入循环条件时还是进入第二个，所以会进入死循环
注意：这⾥找中间元素需要向下取整。因为后续移动左右指针的时候：
- 左指针： left = mid + 1 ，是会向后移动的，因此区间是会缩⼩的；
- 右指针： right = mid ，可能会原地踏步（⽐如：如果向上取整的话，如果剩下 1,2 两个元素， left == 1 ， right == 2 ， mid == 2 。更新区间之后， left，right，mid 的值没有改变，就会陷⼊死循环）。因此⼀定要注意，当 right = mid 的时候，要向下取整。
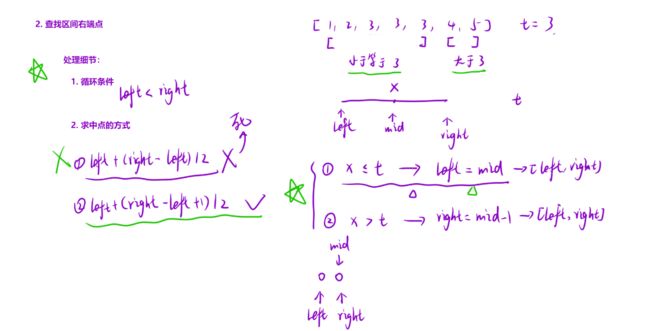
寻找右边界
我们注意到右边界的特点：
- 左边区间（包括右边界） [left, retRight] 都是⼩于等于 x 的；右边区间 [retRight+ 1, right] 都是⼤于 x 的；因此，关于 mid 的落点，我们可以分为下⾯两种情况：
- 当我们的 mid 落在 [left, retRight] 区间的时候，说明 [left, mid - 1]（ mid 不可以舍去，因为有可能是最终结果）都是可以舍去的，此时更新 left 到 mid 的位置；
- 当 mid 落在 [retRight+ 1, right] 的区间的时候，说明 [mid, right] 内的元素是可以舍去的，此时更新 right 到 mid - 1 的位置；
- 由此，就可以通过⼆分，来快速寻找右边界；
- 注意：这⾥找中间元素需要向上取整。因为后续移动左右指针的时候：
- 左指针： left = mid ，可能会原地踏步（⽐如：如果向下取整的话，如果剩下 1,2 两个元素， left == 1， right == 2，mid == 1 。更新区间之后， left，right，mid 的值没有改变，就会陷⼊死循环）。
- 右指针： right = mid - 1 ，是会向前移动的，因此区间是会缩⼩的；因此⼀定要注意，当right = mid 的时候，要向下取整。
代码实现
class Solution
{
public:
vector<int> searchRange(vector<int>& nums, int target)
{
// 处理边界情况
if(nums.size() == 0) return {-1, -1};
int begin = 0;
// 1. ⼆分左端点
int left = 0, right = nums.size() - 1;
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] < target) left = mid + 1;
else right = mid;
}
// 判断是否有结果
if(nums[left] != target) return {-1, -1};
else begin = left; // 标记⼀下左端点
// 2. ⼆分右端点
left = 0, right = nums.size() - 1;
while(left < right)
{
int mid = left + (right - left + 1) / 2;
if(nums[mid] <= target) left = mid;
else right = mid - 1;
}
return {begin, right};
}
};
X的平方根
x的平方根
题目解析
- 返回类型是整数类型，只保留整数部分
- 不允许使用任何内置指数函数和算符
算法原理
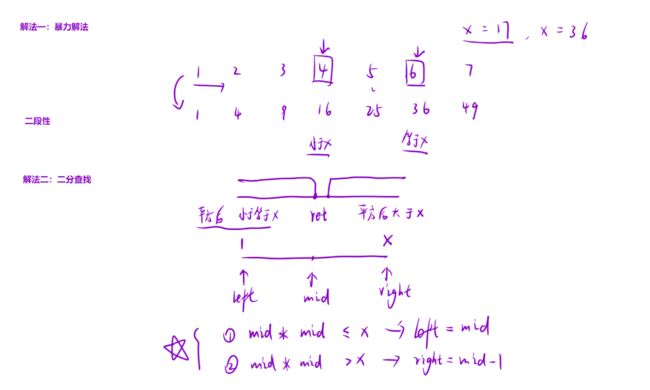
- 暴力解法：从1开始遍历一个一个试。
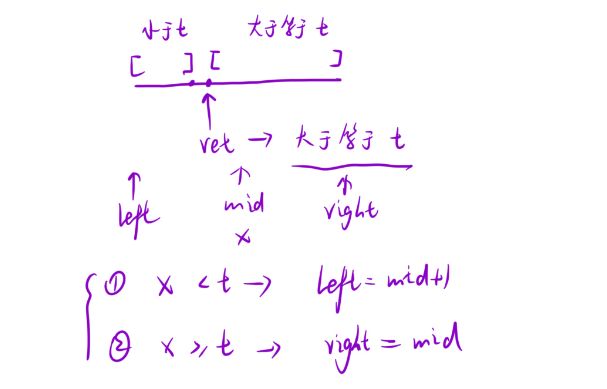
- 二分查找：设ret是x的平方根，最终结果用ret表示，则ret左边的是平方后小于等于x的，右边是大于x的。这时出现二段性，使用二分查找
- 在left移动时，因为left有可能是最终结果（ret左边部分是小于等于的情况），所以不能直接越过mid，所以不能写成mid+1。所以用查找区间右端点的模板
代码实现
class Solution {
public:
int mySqrt(int x)
{
if(x < 1) return 0; // 处理边界情况
int left = 1, right = x;
while(left < right)
{
long long mid = left + (right - left + 1) / 2; // 防溢出
if(mid * mid <= x) left = mid;
else right = mid - 1;
}
return left;
}
};
搜索插入位置
搜索插入位置
题目解析
- 如果能找到，返回数字下标
- 如果找不到，返回该数字应该按照顺序插入的位置下标
- 请必须使用时间复杂度为 O(logn) 的算法。
算法原理
二分查找：
- 插入位置有数：找到，直接返回下标
- 插入位置没数：寻找出现第一个比该数大的位置，或者是数组最后一个位置
综上所述，插入位置ret最终应该大于等于目标值，因此通过ret将数组划分为两个区间，此时发现二段性，用二分查找。所以我们只需要找到大于等于目标值区间的左端点即可。所以我们套用查找区间左端点的模板
当x
代码实现
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] < target) left = mid + 1;
else right = mid;
}
//此时right和left已经相遇，所以这里返回谁都可以
if(nums[left] < target) return right + 1; //插入位置在数组最后一个位置
return right;
}
};
山脉数组的峰顶索引
山脉数组的峰顶索引
题目解析
- 寻找峰值的下标，该题是严格存在山峰数组，只有一个山峰
算法原理
- 暴力解法：从第一个开始遍历，当该数字小于前一个数字，则不是峰值，当第一个出现大于前一个数的，则是峰值。时间复杂度O(n)
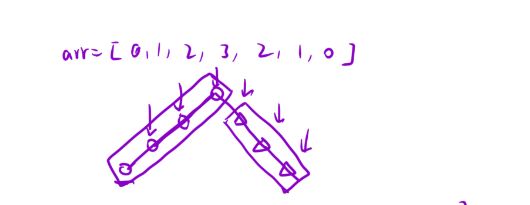
- 优化探寻性质：红色箭头一侧的性质：后一个数字总是大于前一个数字；蓝色箭头一侧的性质：后一个数总是小于前一个数。所以发现二段性，用二分查找（这里我们得出即使数组没有单调性，也可以二分查找）
-
当数字落在红色箭头这一列时，峰值是在这一区间的右端点，所以不能跳过，故更新left位置时，left=mid；
-
当数字落在蓝色箭头这一列时，峰值一定不会在该区域，所以更新right位置时，right = mid-1；
代码实现
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
int left = 1,right = arr.size()-2; //这里不让left=1，right=arr.size()-1是因为不可能在第一个位置
while(left < right)
{
int mid = left+(right-left+1)/2;
if(arr[mid] > arr[mid-1]) left = mid;
else right = mid-1;
}
return left;
}
};
寻找峰值
寻找峰值
该题严格无序数组，可能出现多个山峰的情况
题目解析
- 峰值元素是大于左右相邻两个数；峰值可能有多个，返回任意一个位置的下标即可
- 数组中不会有相邻的相同元素，对于所有有效的 i 都有 nums[i] != nums[i + 1]
算法原理
- 暴力解法：会遇到三种情形：（时间复杂度O(n)）
- 从第一个位置开始走，发现直接开始下降，则第一个位置就是峰值
- 从第一个位置开始，现逐渐上升，后下降，返回下降前的峰值
- 从第一个位置开始，发现一直上升，则返回最后一个位置的下标
- 优化：总体分为两种情况
- 当arr[i] > arr[i+1]（红色箭头），此时左区间一定会存在峰值，右区间可能会存在
- 当arr[i] < arr[i+1]（蓝色箭头），此时右区间一定会存在峰值，左区间可能会存在
故得出二段性，使用二分查找。
- 当arr[i] > arr[i+1]，此时左区间一定有结果(上图，左区间包含i)，则让right去到左区间，故right = mid；
- 当arr[i] < arr[i+1]，此时右区间一定有结果（右区间包含i+1），则让left去到右区间，故right = mid+1；
代码实现
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int left = 0,right = nums.size()-1;
while(left < right)
{
int mid = left+(right-left)/2;
if(nums[mid] > nums[mid+1]) right = mid;
else left = mid+1;
}
return left;
}
};
寻找旋转排序数组中的最小值
寻找旋转排序数组中的最小值
题目解析
- 旋转操作：将最后一个数放到最前面
- 找出数组的最小值,返回该元素
算法原理
-
解法一：暴力解法：遍历查找最小值，时间复杂度为O(n)
-
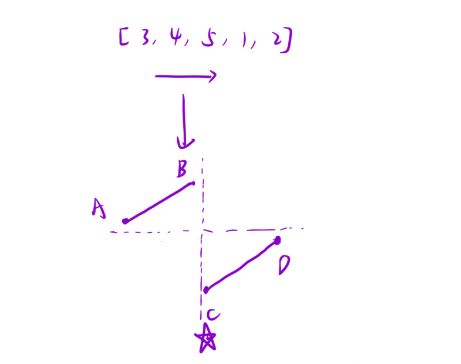
解法二：二分查找：可以把旋转后的数组分为两部分，两部分都是呈现递增的形式，把该问题抽象成折线图，我们会发现明显的二段性，我们以D点作为参照物，会发现折线AB上的值全部大于D点的值，折线CD上的值都小于或等于D点的值。所以我们找到C点对应的值即为最小值即可
- 当mid值落在AB区间时，此时该区间一定不存在最小值，所以在更新left到mid位置时，让left=mid+1
- 当mid值落在CD区间时，此时该区间存在最小值，所以更新right时不能越过mid的位置，让right=mid
代码实现
class Solution {
public:
int findMin(vector<int>& nums) {
int left = 0,right = nums.size()-1;
int x =nums[right]; //表示最后一个位置的值
while(left < right)
{
int mid = left+(right-left)/2;
if(nums[mid] > x) left = mid+1;
else right=mid;
}
return nums[left];
}
};
0~n-1缺失的数字
0~n-1缺失的数字
题目解析
⼀个⻓度为n-1的递增排序数组中的所有数字都是唯⼀的，并且每个数字都在范围0〜n-1之内。在范围0〜n-1内的n个数字中有且只有⼀个数字不在该数组中，请找出这个数字
算法原理
- 解法一：借助容器哈希表：n个数，建立一个n+1大小的哈希表，然后向哈希表里填入，填完后观察哪个位置没有填到，即为确实的数字
- 解法二：直接遍历
- 解法三：位运算：用异或操作，将缺失的数组与正常的数组进行异或（异或操作：相同的数会抵消），缺少的数因为没有对应的数字和它进行异或操作抵消，所以最后异或的结果就是缺少的数。
- 解法四：数学方法——高斯求和公式。先对正常数组进行求和（高中的等差数列），然后依次减去缺失数组的数，剩下的数字即为缺失的数字
以上解法时间复杂度都是O(n)，哈希表解法中还有个O(n)的空间复杂度
-
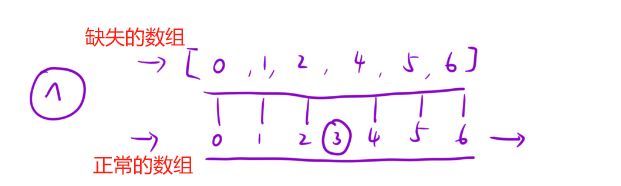
解法五：二分查找：左边区间数组下标的值与正常的数组下标一一对应，右边区间数组中数字下标与正常的不是一一对应；即发现该数组的二段性。我们需要找的结果就在五角星位置，即右边区间最左边的位置
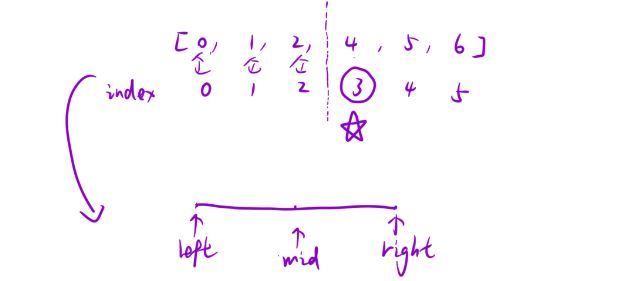
- 当mid落在左边区间时，判读条件为下标值是否一一对应，更新left，left=mid+1；
- 当mid落在右边区间时，更新right，因为mid有可能在最终结果上，所以不能跳过，让right=mid；
- 这里还有个细节问题，如下图这个数组是完全递增的数组，该数组缺少的数字是4，但是我们的二分查找找的是右边区间的左端点。我们发现这个数组根本不存在右区间，此时二分的结果落在了3这个位置，但这个位置的值并不是我们需要的结果，而是该位置的后一个位置。所以最终返回的时候需要判断，当最后left和right相等时，此时所指的位置的值的下标与其相等，说明该数组是一个完全递增的数组，我们缺失的数字时left和right下一个位置。（返回left+1）
代码实现
class Solution {
public:
int takeAttendance(vector<int>& records)
{
int left = 0, right = records.size() - 1;
while(left < right)
{
int mid = left + (right - left) / 2;
if(records[mid] == mid) left = mid + 1;
else right = mid;
}
//返回left和right都行
//处理细节问题
return left == records[left] ? left + 1 : left;
}
};