AI助力智慧农业,基于YOLOv5全系列模型【n/s/m/l/x】开发构建不同参数量级农田场景下庄稼作物、杂草智能检测识别系统
紧接前文,本文是农田场景下庄稼作物、杂草检测识别的第二篇文章,前文是基于YOLOv3这一网络模型实现的目标检测,v3相对来说比较早期的网络模型了,本文是基于最为经典的YOLOv5来开发不同参数量级的检测端模型。
首先看下实例效果:
YOLOv3(You Only Look Once version 3)是一种基于深度学习的快速目标检测算法,由Joseph Redmon等人于2018年提出。它的核心技术原理和亮点如下:
-
技术原理:
- YOLOv3采用单个神经网络模型来完成目标检测任务。与传统的目标检测方法不同,YOLOv3将目标检测问题转化为一个回归问题,通过卷积神经网络输出图像中存在的目标的边界框坐标和类别概率。
- YOLOv3使用Darknet-53作为骨干网络,用来提取图像特征。检测头(detection head)负责将提取的特征映射到目标边界框和类别预测。
-
亮点:
- YOLOv3在保持较高的检测精度的同时,能够实现非常快的检测速度。相较于一些基于候选区域的目标检测算法(如Faster R-CNN、SSD等),YOLOv3具有更高的实时性能。
- YOLOv3对小目标和密集目标的检测效果较好,同时在大目标的检测精度上也有不错的表现。
- YOLOv3具有较好的通用性和适应性,适用于各种目标检测任务,包括车辆检测、行人检测等。
相比之下,YOLOv5是在YOLOv3的基础上进行了改进。YOLOv5的技术原理和亮点包括:
-
技术原理:
- YOLOv5同样采用单个神经网络模型来完成目标检测任务,但采用了新的神经网络架构,融合了领先的轻量级模型设计理念。
- YOLOv5使用较小的骨干网络和新的检测头设计,以实现更快的推断速度,并在不降低精度的前提下提高目标检测的准确性。
-
亮点:
- YOLOv5在模型结构上进行了改进,引入了更先进的轻量级网络架构,因此在速度和精度上都有所提升。
- YOLOv5支持更灵活的模型大小和预训练选项,可以根据任务需求选择不同大小的模型,同时提供丰富的数据增强扩展、模型集成等方法来提高检测精度。
- YOLOv5通过使用更简洁的代码实现,提高了模型的易用性和可扩展性。
YOLOv5是一种快速、准确的目标检测模型,由Glen Darby于2020年提出。其主要特点和技术原理如下:
-
YOLO(You Only Look Once)技术原理:
- YOLOv5的核心思想是将目标检测任务转化为一个回归问题。它采用单个神经网络模型,将输入图像分割成网格,并利用卷积神经网络输出每个网格中存在的目标的边界框坐标和类别概率。
- YOLOv5使用骨干网络(backbone network)来提取特征,然后将这些特征送入检测头(detection head)来进行目标检测。
-
特点和亮点:
- YOLOv5的主要亮点之一是其简单、高效的设计。它采用的是单阶段检测器,直接在单个模型中完成目标检测任务,没有独立的区域提议(region proposal)和后处理步骤。
- YOLOv5具有出色的性能和速度。它在保持高精度的同时能够实现实时目标检测,适用于各种实际场景。
- YOLOv5提供了多种不同的预训练模型和大小,可以根据特定的应用场景选择合适的模型。同时,它支持在不同任务上进行微调(fine-tuning)。
-
技术细节:
- YOLOv5使用了较小的backbone网络(如CSPDarknet53、CSPDarknet53-tiny等),以便实现更快的推理速度。
- YOLOv5在训练过程中采用了类别平衡的策略,以解决数据不平衡带来的问题。
- YOLOv5的推理性能得到了显著的提升,特别是在目标检测精度和处理速度方面取得了很好的平衡。
简单看下数据集:
训练数据配置文件如下所示:
# Dataset
path: ./dataset
train:
- images/train
val:
- images/test
test:
- images/test
# Classes
names:
0: crop
1: weed本文将YOLOv5系列五款不同参数量级的模型均进行了开发评测,接下来依次看下模型详情:
【yolov5n】
# YOLOv5 by Ultralytics, GPL-3.0 license
# Parameters
nc: 2 # number of classes
depth_multiple: 0.33 # model depth multiple
width_multiple: 0.25 # layer channel multiple
anchors:
- [10,13, 16,30, 33,23] # P3/8
- [30,61, 62,45, 59,119] # P4/16
- [116,90, 156,198, 373,326] # P5/32
# YOLOv5 v6.0 backbone
backbone:
# [from, number, module, args]
[[-1, 1, Conv, [64, 6, 2, 2]], # 0-P1/2
[-1, 1, Conv, [128, 3, 2]], # 1-P2/4
[-1, 3, C3, [128]],
[-1, 1, Conv, [256, 3, 2]], # 3-P3/8
[-1, 6, C3, [256]],
[-1, 1, Conv, [512, 3, 2]], # 5-P4/16
[-1, 9, C3, [512]],
[-1, 1, Conv, [1024, 3, 2]], # 7-P5/32
[-1, 3, C3, [1024]],
[-1, 1, SPPF, [1024, 5]], # 9
]
# YOLOv5 v6.0 head
head:
[[-1, 1, Conv, [512, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, 'nearest']],
[[-1, 6], 1, Concat, [1]], # cat backbone P4
[-1, 3, C3, [512, False]], # 13
[-1, 1, Conv, [256, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, 'nearest']],
[[-1, 4], 1, Concat, [1]], # cat backbone P3
[-1, 3, C3, [256, False]], # 17 (P3/8-small)
[-1, 1, Conv, [256, 3, 2]],
[[-1, 14], 1, Concat, [1]], # cat head P4
[-1, 3, C3, [512, False]], # 20 (P4/16-medium)
[-1, 1, Conv, [512, 3, 2]],
[[-1, 10], 1, Concat, [1]], # cat head P5
[-1, 3, C3, [1024, False]], # 23 (P5/32-large)
[[17, 20, 23], 1, Detect, [nc, anchors]], # Detect(P3, P4, P5)
]
【yolov5s】
# YOLOv5 by Ultralytics, GPL-3.0 license
# Parameters
nc: 2 # number of classes
depth_multiple: 0.33 # model depth multiple
width_multiple: 0.50 # layer channel multiple
anchors:
- [10,13, 16,30, 33,23] # P3/8
- [30,61, 62,45, 59,119] # P4/16
- [116,90, 156,198, 373,326] # P5/32
#Backbone
backbone:
# [from, number, module, args]
[[-1, 1, Conv, [64, 6, 2, 2]], # 0-P1/2
[-1, 1, Conv, [128, 3, 2]], # 1-P2/4
[-1, 3, C3, [128]],
[-1, 1, Conv, [256, 3, 2]], # 3-P3/8
[-1, 6, C3, [256]],
[-1, 1, Conv, [512, 3, 2]], # 5-P4/16
[-1, 9, C3, [512]],
[-1, 1, Conv, [1024, 3, 2]], # 7-P5/32
[-1, 3, C3, [1024]],
[-1, 1, SPPF, [1024, 5]], # 9
]
#Head
head:
[[-1, 1, Conv, [512, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, 'nearest']],
[[-1, 6], 1, Concat, [1]], # cat backbone P4
[-1, 3, C3, [512, False]], # 13
[-1, 1, Conv, [256, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, 'nearest']],
[[-1, 4], 1, Concat, [1]], # cat backbone P3
[-1, 3, C3, [256, False]], # 17 (P3/8-small)
[-1, 1, Conv, [256, 3, 2]],
[[-1, 14], 1, Concat, [1]], # cat head P4
[-1, 3, C3, [512, False]], # 20 (P4/16-medium)
[-1, 1, Conv, [512, 3, 2]],
[[-1, 10], 1, Concat, [1]], # cat head P5
[-1, 3, C3, [1024, False]], # 23 (P5/32-large)
[[17, 20, 23], 1, Detect, [nc, anchors]], # Detect(P3, P4, P5)
]
【yolov5m】
# YOLOv5 by Ultralytics, GPL-3.0 license
# Parameters
nc: 2 # number of classes
depth_multiple: 0.67 # model depth multiple
width_multiple: 0.75 # layer channel multiple
anchors:
- [10,13, 16,30, 33,23] # P3/8
- [30,61, 62,45, 59,119] # P4/16
- [116,90, 156,198, 373,326] # P5/32
# YOLOv5 v6.0 backbone
backbone:
# [from, number, module, args]
[[-1, 1, Conv, [64, 6, 2, 2]], # 0-P1/2
[-1, 1, Conv, [128, 3, 2]], # 1-P2/4
[-1, 3, C3, [128]],
[-1, 1, Conv, [256, 3, 2]], # 3-P3/8
[-1, 6, C3, [256]],
[-1, 1, Conv, [512, 3, 2]], # 5-P4/16
[-1, 9, C3, [512]],
[-1, 1, Conv, [1024, 3, 2]], # 7-P5/32
[-1, 3, C3, [1024]],
[-1, 1, SPPF, [1024, 5]], # 9
]
# YOLOv5 v6.0 head
head:
[[-1, 1, Conv, [512, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, 'nearest']],
[[-1, 6], 1, Concat, [1]], # cat backbone P4
[-1, 3, C3, [512, False]], # 13
[-1, 1, Conv, [256, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, 'nearest']],
[[-1, 4], 1, Concat, [1]], # cat backbone P3
[-1, 3, C3, [256, False]], # 17 (P3/8-small)
[-1, 1, Conv, [256, 3, 2]],
[[-1, 14], 1, Concat, [1]], # cat head P4
[-1, 3, C3, [512, False]], # 20 (P4/16-medium)
[-1, 1, Conv, [512, 3, 2]],
[[-1, 10], 1, Concat, [1]], # cat head P5
[-1, 3, C3, [1024, False]], # 23 (P5/32-large)
[[17, 20, 23], 1, Detect, [nc, anchors]], # Detect(P3, P4, P5)
]
【yolov5l】
# YOLOv5 by Ultralytics, GPL-3.0 license
# Parameters
nc: 2 # number of classes
depth_multiple: 1.0 # model depth multiple
width_multiple: 1.0 # layer channel multiple
anchors:
- [10,13, 16,30, 33,23] # P3/8
- [30,61, 62,45, 59,119] # P4/16
- [116,90, 156,198, 373,326] # P5/32
# YOLOv5 v6.0 backbone
backbone:
# [from, number, module, args]
[[-1, 1, Conv, [64, 6, 2, 2]], # 0-P1/2
[-1, 1, Conv, [128, 3, 2]], # 1-P2/4
[-1, 3, C3, [128]],
[-1, 1, Conv, [256, 3, 2]], # 3-P3/8
[-1, 6, C3, [256]],
[-1, 1, Conv, [512, 3, 2]], # 5-P4/16
[-1, 9, C3, [512]],
[-1, 1, Conv, [1024, 3, 2]], # 7-P5/32
[-1, 3, C3, [1024]],
[-1, 1, SPPF, [1024, 5]], # 9
]
# YOLOv5 v6.0 head
head:
[[-1, 1, Conv, [512, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, 'nearest']],
[[-1, 6], 1, Concat, [1]], # cat backbone P4
[-1, 3, C3, [512, False]], # 13
[-1, 1, Conv, [256, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, 'nearest']],
[[-1, 4], 1, Concat, [1]], # cat backbone P3
[-1, 3, C3, [256, False]], # 17 (P3/8-small)
[-1, 1, Conv, [256, 3, 2]],
[[-1, 14], 1, Concat, [1]], # cat head P4
[-1, 3, C3, [512, False]], # 20 (P4/16-medium)
[-1, 1, Conv, [512, 3, 2]],
[[-1, 10], 1, Concat, [1]], # cat head P5
[-1, 3, C3, [1024, False]], # 23 (P5/32-large)
[[17, 20, 23], 1, Detect, [nc, anchors]], # Detect(P3, P4, P5)
]
【yolov5x】
# YOLOv5 by Ultralytics, GPL-3.0 license
# Parameters
nc: 2 # number of classes
depth_multiple: 1.33 # model depth multiple
width_multiple: 1.25 # layer channel multiple
anchors:
- [10,13, 16,30, 33,23] # P3/8
- [30,61, 62,45, 59,119] # P4/16
- [116,90, 156,198, 373,326] # P5/32
# YOLOv5 v6.0 backbone
backbone:
# [from, number, module, args]
[[-1, 1, Conv, [64, 6, 2, 2]], # 0-P1/2
[-1, 1, Conv, [128, 3, 2]], # 1-P2/4
[-1, 3, C3, [128]],
[-1, 1, Conv, [256, 3, 2]], # 3-P3/8
[-1, 6, C3, [256]],
[-1, 1, Conv, [512, 3, 2]], # 5-P4/16
[-1, 9, C3, [512]],
[-1, 1, Conv, [1024, 3, 2]], # 7-P5/32
[-1, 3, C3, [1024]],
[-1, 1, SPPF, [1024, 5]], # 9
]
# YOLOv5 v6.0 head
head:
[[-1, 1, Conv, [512, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, 'nearest']],
[[-1, 6], 1, Concat, [1]], # cat backbone P4
[-1, 3, C3, [512, False]], # 13
[-1, 1, Conv, [256, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, 'nearest']],
[[-1, 4], 1, Concat, [1]], # cat backbone P3
[-1, 3, C3, [256, False]], # 17 (P3/8-small)
[-1, 1, Conv, [256, 3, 2]],
[[-1, 14], 1, Concat, [1]], # cat head P4
[-1, 3, C3, [512, False]], # 20 (P4/16-medium)
[-1, 1, Conv, [512, 3, 2]],
[[-1, 10], 1, Concat, [1]], # cat head P5
[-1, 3, C3, [1024, False]], # 23 (P5/32-large)
[[17, 20, 23], 1, Detect, [nc, anchors]], # Detect(P3, P4, P5)
]
在实验训练开发阶段,所有的模型均保持完全相同的参数设置,等待训练完成后,来整体进行评测对比分析。
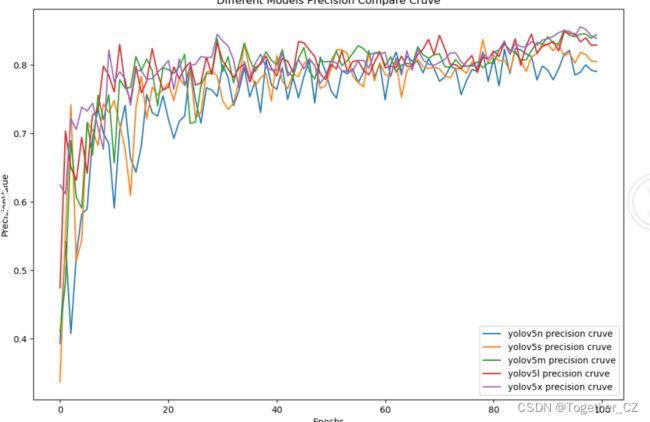
【Precision曲线】
精确率曲线(Precision-Recall Curve)是一种用于评估二分类模型在不同阈值下的精确率性能的可视化工具。它通过绘制不同阈值下的精确率和召回率之间的关系图来帮助我们了解模型在不同阈值下的表现。
精确率(Precision)是指被正确预测为正例的样本数占所有预测为正例的样本数的比例。召回率(Recall)是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。
绘制精确率曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的精确率和召回率。
将每个阈值下的精确率和召回率绘制在同一个图表上,形成精确率曲线。
根据精确率曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
通过观察精确率曲线,我们可以根据需求确定最佳的阈值,以平衡精确率和召回率。较高的精确率意味着较少的误报,而较高的召回率则表示较少的漏报。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
精确率曲线通常与召回率曲线(Recall Curve)一起使用,以提供更全面的分类器性能分析,并帮助评估和比较不同模型的性能。
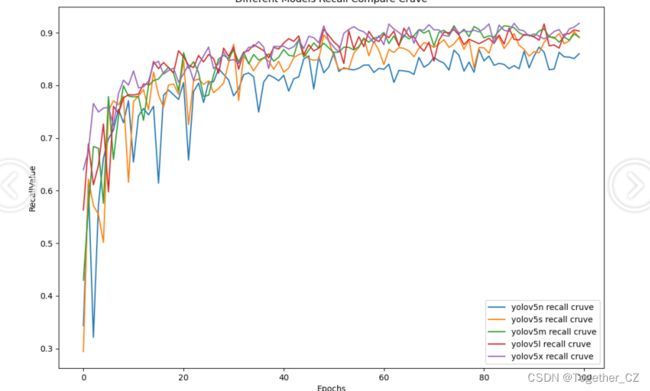
【Recall曲线】
召回率曲线(Recall Curve)是一种用于评估二分类模型在不同阈值下的召回率性能的可视化工具。它通过绘制不同阈值下的召回率和对应的精确率之间的关系图来帮助我们了解模型在不同阈值下的表现。
召回率(Recall)是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。召回率也被称为灵敏度(Sensitivity)或真正例率(True Positive Rate)。
绘制召回率曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的召回率和对应的精确率。
将每个阈值下的召回率和精确率绘制在同一个图表上,形成召回率曲线。
根据召回率曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
通过观察召回率曲线,我们可以根据需求确定最佳的阈值,以平衡召回率和精确率。较高的召回率表示较少的漏报,而较高的精确率意味着较少的误报。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
召回率曲线通常与精确率曲线(Precision Curve)一起使用,以提供更全面的分类器性能分析,并帮助评估和比较不同模型的性能。
【F1值曲线】
F1值曲线是一种用于评估二分类模型在不同阈值下的性能的可视化工具。它通过绘制不同阈值下的精确率(Precision)、召回率(Recall)和F1分数的关系图来帮助我们理解模型的整体性能。
F1分数是精确率和召回率的调和平均值,它综合考虑了两者的性能指标。F1值曲线可以帮助我们确定在不同精确率和召回率之间找到一个平衡点,以选择最佳的阈值。
绘制F1值曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的精确率、召回率和F1分数。
将每个阈值下的精确率、召回率和F1分数绘制在同一个图表上,形成F1值曲线。
根据F1值曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
F1值曲线通常与接收者操作特征曲线(ROC曲线)一起使用,以帮助评估和比较不同模型的性能。它们提供了更全面的分类器性能分析,可以根据具体应用场景来选择合适的模型和阈值设置。
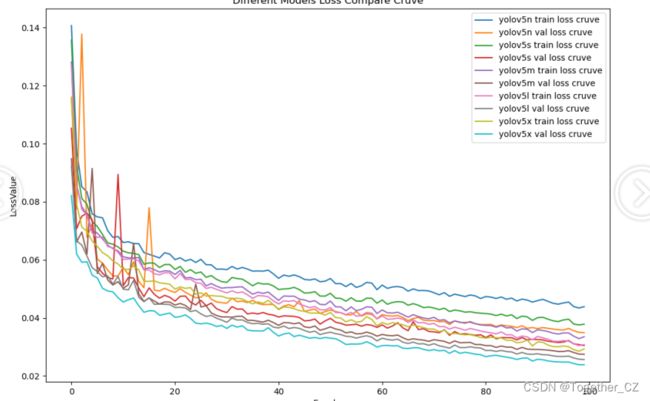
【loss对比曲线】
整体对比分析不难发现:在本文我们自主构建的作物、杂草检测的数据集上五款不同参数量级的模型没有呈现出来断崖式的性能差异,纵向对比来看:n系列的模型性能最差,s系列次之,而m、l和x三个系列的模型则达到了相近的水平,结合推理速度来考虑的话实际项目中更加倾向于优先选择使用m系列的模型。