图搜索算法（深度优先、广度优先）

一、图论

教学的一个分支，它以图为研究对象。

图论中的图是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。

图的结构

非线性结构

有n个直接前驱，n个直接后继

图的组成

由两部分组成，一部分叫点的集合，另一部分叫边的集合

图的分类

1）无向图：图中的边是节点的无序对（即两节点不分谁是起始点，谁是终止点），则称此图为无向图。通常用圆括号表示无向边。

2）有向图：图中的边是节点的有序树，则称此图为有向图。有向边又称为弧，通常用尖括号表示一条有向边。

弧头：弧的终止节点

弧尾：弧的开始节点

3）有向完全图与无向完全图。在图中的任意一个点，和其它所有的点都有边连接。

二、深度优先

深度优先规则

沿着一个固定的方向进行行走，到了岔路口才又一次选择方向，如果碰到了死胡同退回上一个岔路口重新选择方向，走过的路就不会再重新走，一次走一个岔路口

注意：因为方向设定不一样，可能最终找到路径是不一样的

代码示例

#include 
#include 
using namespace std;

//1. 地图的大小
#define MAP_ROW 10
#define MAP_COL 10
//2. 坐标点
struct Point
{
    int row,col;
};
//3. 方向
enum PathDir
{
    p_up,p_left,p_down,p_right
};
//4. 辅助数组中的路径点
struct PathData
{
    int val;//原始数组路经点信息
    bool isFind;//路径点是否已经访问过
    PathDir dir;//路径点行进方向
};
//---探路判断---
bool isMove(PathData arr[][MAP_COL],int row,int col)
{
    //1. 越界
    if (row<0 || row > MAP_ROW || col<0 || col>MAP_COL)
        return false;
    //2. 没有障碍物，且没有被访问
    if (arr[row][col].val==0 && arr[row][col].isFind==false)
        return true;
    //3. 可能已访问，可能是障碍
    return false;
}

int main()
{
    //5. 准备二维数组
    int arr[MAP_ROW][MAP_COL] = {
        {1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 },
        {1 ,0 ,1 ,1 ,1 ,1 ,1 ,1 ,0 ,1 },
        {1 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,1 },
        {1 ,1 ,1 ,0 ,1 ,0 ,1 ,1 ,1 ,1 },
        {1 ,0 ,1 ,0 ,1 ,0 ,0 ,0 ,1 ,1 },
        {1 ,0 ,0 ,0 ,1 ,1 ,0 ,1 ,1 ,1 },
        {1 ,1 ,0 ,1 ,1 ,1 ,0 ,0 ,1 ,1 },
        {1 ,1 ,0 ,1 ,1 ,1 ,1 ,0 ,0 ,1 },
        {1 ,0 ,0 ,0 ,1 ,1 ,1 ,1 ,0 ,1 },
        {1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 }
    };
    //6. 准备辅助数组表示地图
    PathData pathArr[MAP_ROW][MAP_COL];
    //7. 初始化辅助数组
    for (int i = 0; i < MAP_ROW; i++)
    {
        for (int j = 0; j < MAP_COL; j++)
        {
            pathArr[i][j].val = arr[i][j];//路径点信息
            pathArr[i][j].isFind = false;//每个位置都还没被访问
            pathArr[i][j].dir = p_up;//自定义方向先向上
        }
    }
    //8. 准备起点和终点
    Point begPoint = {1,1};
    Point endPoint = {8,8};
    //9. 准备容器保存路径点
    stack ms;
    ms.push(begPoint);
    //10. 辅助坐标点，用来查询后续节点
    Point currPoint = begPoint;
    //11. 开始寻路
    while (true)
    {
        switch (pathArr[currPoint.row][currPoint.col].dir)
        {
        case p_up:
                //第一步：先改变方向（下一个方向）
                pathArr[currPoint.row][currPoint.col].dir = p_left;
                //第二步：探索下一个路径点
                if (isMove(pathArr,currPoint.row-1,currPoint.col))
                {
                    //第三步：改变当前路径点已访问
                    pathArr[currPoint.row][currPoint.col].isFind = true;
                    //第四步：下一路径点入栈
                    Point tempPoint = {currPoint.row-1,currPoint.col};
                    ms.push(tempPoint);
                    //第五步：下一路径点改为当前路径点
                    currPoint = tempPoint;
                }
            break;
        case p_left:
                pathArr[currPoint.row][currPoint.col].dir = p_down;
                if (isMove(pathArr,currPoint.row,currPoint.col-1))
                {
                    pathArr[currPoint.row][currPoint.col].isFind = true;
                    Point tempPoint = {currPoint.row,currPoint.col-1};
                    ms.push(tempPoint);
                    currPoint = tempPoint;
                }
            break;
        case p_down:
                pathArr[currPoint.row][currPoint.col].dir = p_right;
                if (isMove(pathArr,currPoint.row+1,currPoint.col))
                {
                    pathArr[currPoint.row][currPoint.col].isFind = true;
                    Point tempPoint = {currPoint.row+1,currPoint.col};
                    ms.push(tempPoint);
                    currPoint = tempPoint;
                }
            break;
        case p_right:
                //这是最后一个方向
                if (isMove(pathArr,currPoint.row,currPoint.col+1))
                {
                    pathArr[currPoint.row][currPoint.col].isFind = true;
                    Point tempPoint = {currPoint.row,currPoint.col+1};
                    ms.push(tempPoint);
                    currPoint = tempPoint;
                }
                //下一路径点不能走（死胡同）
                else
                {
                    //第一步：改变当前路径点已访问
                    Point tempPoint = ms.top();
                    pathArr[tempPoint.row][tempPoint.col].isFind = true;
                    //第二步：退栈，找到上一个路径点
                    ms.pop();
                    //第三步：上一路径点改为当前路径点（若栈不为空）
                    if (!ms.empty())
                    {
                        currPoint = ms.top();
                    }
                }
            break;
        }
        //结束条件一：找到路
        if (currPoint.row==endPoint.row && currPoint.col==endPoint.col)
        {
            break;
        }
        //结束条件二：没有路（容器为空）
        if (ms.empty())
        {
            break;
        }
    }
    //12. 寻路终止，打印路径
    while (!ms.empty())
    {
        //第一步：打印栈顶元素
        Point tempPoint = ms.top();
        printf("row==%d---col==%d\n",tempPoint.row,tempPoint.col);
        //第二步：退栈
        ms.pop();
    }

    return 0;
}

三、广度优先

广度优先规则

1）走直线，不能走斜线

2）理解为树的层次次序

3）如果有路，必然找到最短路径

4）需要遍历所有可通行的节点，如果地图比较大，开销就比较大

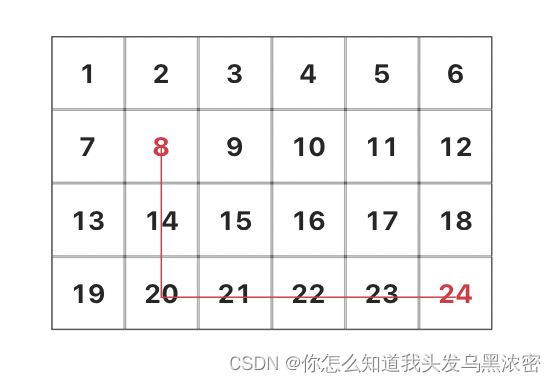
搜索过程图示

  

代码示例

#include 
#include 
using namespace std;

//1. 地图的大小
#define MAP_ROW 4
#define MAP_COL 6
//2. 坐标点
struct Point
{
    int row,col;
};
//3. 方向
enum PathDir
{
    p_up,p_left,p_down,p_right
};
//4. 辅助数组中的路径点
struct PathData
{
    int val;
    bool isFind;
    PathDir dir;
};
//5.树形结构的节点
struct PathNode
{
    Point pos;
    PathNode *parentNode;
    vector childNode;
};
//---探路判断---
bool isFind(PathData arr[][MAP_COL],Point pos)
{
    //1. 越界
    if (pos.row<0 || pos.row>=MAP_ROW || pos.col<0 || pos.col>=MAP_COL)
        return false;
    //2. 没有障碍物，且没有被访问
    if (arr[pos.row][pos.col].val==0 && arr[pos.row][pos.col].isFind==false)
        return true;
    //3. 可能已访问，可能是障碍
    return false;
}
//---清空树形节点---
void clearNode(PathNode *& root)//注意引用！！！
{
    if (root)
    {
        //第一步：循环子次序
        for (int i = 0; i < (int)root->childNode.size(); i++)
        {
            //第二步：递归节点的子节点
            clearNode(root->childNode[i]);
        }
        //第三步：清除节点
        delete root;
        root = nullptr;
    }
}

int main()
{
    //6. 准备二维数组
    int arr[MAP_ROW][MAP_COL] = {
        {0 ,0 ,0 ,0 ,0 ,0 },
        {0 ,0 ,0 ,0 ,0 ,0 },
        {0 ,0 ,0 ,0 ,0 ,0 },
        {0 ,0 ,0 ,0 ,0 ,0 }
    };
    //7. 准备辅助数组表示地图
    PathData pathArr[MAP_ROW][MAP_COL];
    //8. 初始化辅助数组
    for (int i = 0; i < MAP_ROW; i++)
    {
        for (int j = 0; j < MAP_COL; j++)
        {
            pathArr[i][j].val = arr[i][j];//路径点信息
            pathArr[i][j].isFind = false;//每个位置都还没被访问
            pathArr[i][j].dir = p_up;//自定义方向先向上
        }
    }
    //9. 准备起点和终点
    Point begPoint = {1,1};
    Point endPoint = {3,5};
    //10. 开辟根节点
    PathNode *pRoot = new PathNode;
    pRoot->pos = begPoint;
    pRoot->parentNode = nullptr;
    //11. 根节点已访问
    pathArr[begPoint.row][begPoint.col].isFind = true;
    //12. 准备两个辅助数组，保存树形结构中父子次序的节点
    vector currList;//当前搜索的父次序
    vector tempList;//当前搜索的父次序的子次序
    //13. 将根节点插入当前搜索父次序
    currList.push_back(pRoot);
    //14. 开始寻路
    while (true)
    {
        //第一步：循环父次序
        for (int i = 0; i < (int)currList.size(); i++)
        {
            //第二步：循环方向
            for (int j = 0; j < 4; j++)
            {
                Point tempPoint = currList[i]->pos;
                switch (j)
                {
                case p_up:
                        tempPoint.row--;
                    break;
                case p_left:
                        tempPoint.col--;
                    break;
                case p_down:
                        tempPoint.row++;
                    break;
                case p_right:
                        tempPoint.col++;
                    break;
                }
                //第三步：探索下一个路径点
                if (isFind(pathArr,tempPoint))
                {
                    //第四步：改变当前路径点已访问
                    pathArr[tempPoint.row][tempPoint.col].isFind = true;
                    //第五步：开辟树形节点
                    PathNode *tempNode = new PathNode;
                    tempNode->pos = tempPoint;
                    //第六步：关联父子关系
                    tempNode->parentNode = currList[i];
                    currList[i]->childNode.push_back(tempNode);
                    //第七步：将下一路径点插入子次序
                    tempList.push_back(tempNode);
                    //---寻路终止，打印路径---
                    if (tempPoint.row==endPoint.row && 
                        tempPoint.col==endPoint.col)
                    {
                        PathNode *pNode = tempNode;
                        while (pNode)
                        {
                            printf("row==%d---col==%d\n",
                                    pNode->pos.row,pNode->pos.col);
                            //父节点遍历打印路径
                            pNode = pNode->parentNode;
                        }
                        goto OVERTAB;//跳出循环
                    }
                }
            }
        }
        //结束条件：没有路
        if (tempList.empty())
        {
            break;
        }
        //把子次序赋值给父次序
        currList = tempList;
        tempList.clear();//记得清空
    }
    OVERTAB:
    //清空根节点（使用goto跳转语句，清空堆内存）
    clearNode(pRoot);

    return 0;
}