微积分-第一章函数(合集)
第一章函数
1.1 函数的定义
简单来说,函数就是一种规则,它将一个值作为输入映射到另一个值作为输出。如 f ( x ) = 5 x f(x)=5x f(x)=5x。其中f称为函数, 5 x 5x 5x 是将输入 x x x映射到输出的规则, f ( x ) f(x) f(x)称为函数值或输出, x x x称为输入。这个函数就是接受x作为输入,将x乘以5作为值输出。
输入x来自于称为定义域的集合注。输出来自称为值域的集合。
让我们看更多函数的例子:
- 令 f ( x ) = 5 x 3 f(x)=5x^3 f(x)=5x3,大家可以尝试自己划分这个函数中的各个部分。如果没有明确说明定义域,则默认定义域尽可能包括实数集更多的部分。对于这个例子来说就是实数集R。那值域呢?让我们看函数的映射规则,这个函数的规则是:将任何数变为自己的立方并乘以5。值域是所有可能输出的所组成的集合。这个映射规则的输出实数集R中的任意内容。而定义域是R,所以它的值域也是R。
- 我们再来看函数 g ( x ) = x g(x)=\sqrt{x} g(x)=x,它的定义域是什么呢?我们知道平方根下的数必须大于等于0,所以它的定义域应该也是大于等于0。用集合表示则是 { x ∣ x ≥ 0 , x ∈ R } \{x|x \geq 0, x \in R\} {x∣x≥0,x∈R}。由于平方根函数将非负实数映射到非负实数,所以它的值域自然也是非负数。
- 考虑函数 h ( x ) = 1 x h(x)=\frac{1}{x} h(x)=x1。我们知道分数的分母不能为0,所以它的定义域是 { x ∣ x ! = 0 } \{x|x != 0\} {x∣x!=0}。我们称函数 h h h在 x = 0 x=0 x=0处没有定义。
- 考虑两个函数 f ( x ) = x 2 x f(x)=\frac{x^2}{x} f(x)=xx2和 h ( x ) = x h(x)={x} h(x)=x。它们是同一个函数吗?或许有人认为,函数 f f f可以简化为 f ( x ) = x f(x)=x f(x)=x,所以 f f f等于 h h h。这是不完全对的,正确的说法是:函数 f f f简化为 f ( x ) = x f(x)=x f(x)=x,当且仅当 x ≠ 0 x \neq 0 x=0。这是因为分母不为0,在x=0时函数无定义。所以,虽然函数 f ( x ) = x 2 x f(x)=\frac{x^2}{x} f(x)=xx2 和函数 h ( x ) = x h(x)=x h(x)=x 在大部分情况下有相同的值,但由于在 x = 0 x=0 x=0 时 f ( x ) f(x) f(x) 是未定义的,所以我们不能说 f f f 和 h h h 是完全相同的函数。我们在考虑函数的时候一定不可以抛开定义域。所以我们不能说函数 f f f等于函数 h h h。那么怎么让函数 h h h等于函数 f f f呢?很简单限制它的定义域为 { x ∣ x ≠ 0 } \{x | x \neq 0\} {x∣x=0}就可以了。只有当两个函数的映射规则和它的定义域同时相等时,这两个函数才相等。
我们来总结一下要点:
- 如果一个函数没有明确说明定义域,则默认定义域尽可能包括实数集更多的部分。
- 值域是所有可能输出的所组成的集合。
- 函数是一种映射,更为准确的说:函数被定义为从一个集合(称为定义域)到另一个集合(称为值域)的唯一映射。这意味着,定义域中的每一个元素,都会通过函数被映到射值域中唯一确定的元素。一个函数对于同一个输入不会存在两个或更多个输出。
- 在数学中,如果两个函数在相同的定义域内有相同的映射规则(即,对于定义域内的每一个输入,两个函数都给出相同的输出),那么我们可以说这两个函数是相等的。
1.2 函数的定义域
在上一节中说到,如果一个函数没有明确说明定义域,则默认定义域尽可能包括实数集更多的部分。这一节我们具体讲一下如何求解定义域。
求解函数的定义域,就是要找出函数的规则中所不能接收的值(导致函数无法计算的值)构成的集合S,我们再取集合S相对于实数集R的补集注。这个补集就是函数的定义域。
这里列举一些常见的情况:
- 分式:分式的分母不能为0
- 平方根:平方根下的数必须大于0。不只是平方根,对于四次方根、六次方根等等,这些偶次方根下的数都必须大于0.
- 对数注:对数的底数必须大于0且不等于1的实数,真数必须大于0
考虑函数 f ( x ) = x x − 2 f(x)=\frac{\sqrt{x}}{x-2} f(x)=x−2x的定义域是什么?
我们可以看到式子中出现了分式,那么我们就需要注意分母不能为0。这里式子的分母是 x − 2 x-2 x−2,所以 x ≠ 2 x \neq 2 x=2。处理完了分母,再来看分子。分子中出现了根号。这说明 x ≥ 0 x \geq 0 x≥0。综上所述我们有 x ≠ 2 x \neq 2 x=2且 x ≥ 0 x \geq 0 x≥0。这用集合表示为 { x ∣ x ≠ 2 且 x ≥ 0 , x ∈ R } \{x|x \neq 2 且x \geq 0,x \in R\} {x∣x=2且x≥0,x∈R}。
我们通常不使用集合描述定义域而是使用区间描述。上述定义域可以用区间注描述为 [ 0 , 2 ) ∪ ( 2 , + ∞ ) [0,2) \cup(2,+\infty) [0,2)∪(2,+∞)。
让我们来看更难一点的例子
f ( x ) = l o g 2 ( x − 5 ) x 2 + x − 6 f(x)=\frac{log_{2}(x-5)}{\sqrt{x^2+x-6}} f(x)=x2+x−6log2(x−5)
这是一个分式,分母不能为0,即 x 2 + x − 6 ≠ 0 \sqrt{x^2+x-6} \neq 0 x2+x−6=0。且平方根下必须大于等于0,所以需要
x 2 + x − 6 > 0 x^2+x-6 > 0 x2+x−6>0
求解这个不等式得到 x > 2 x >2 x>2。
我们在看来分子,分子是一个对数。对数的真数大于0,所以需要
x − 5 > 0 x-5>0 x−5>0
即 x > 5 x >5 x>5。这个函数的定义域就是 x > 2 x >2 x>2和 x > 5 x >5 x>5的交集: ( 5 , + ∞ ) (5,+\infty) (5,+∞)
1.3 反函数
反函数顾名思义就是将原函数的输出逆反回原函数输入的函数。反函数的输入是原函数的输出,反函数的输出就是原函数的输入。函数 f f f的反函数,记作 f − 1 ( y ) f^{-1}(y) f−1(y)。
考虑函数 f ( x ) = 5 x + 2 f(x)=5x+2 f(x)=5x+2,想要求得在 f f f的定义域中哪个x满足 f ( x ) f(x) f(x),就可以使用反函数 f − 1 ( y ) = y − 2 5 f^{-1}(y)=\frac{y-2}{5} f−1(y)=5y−2。
需要注意的是,并不是每个函数都具有反函数。这是因为在原函数中可能存在两个或更多的输入x对应同一个输出y。在之前的1.1节中,我们说过函数要求定义域中的每一个输入必须有唯一确定的输出与之对应。所以对于上述情况中的函数并不具备反函数。只有在值域中的任意y值都在定义域中有唯一确定的x值,满足 f ( x ) = y f(x)=y f(x)=y的函数就会反函数。
我们来总结一下:
- 从一个函数 f f f出发,使得对于 f f f的值域内任意y值,在定义域内都有唯一确定的x值,满足 f ( x ) = y f(x)=y f(x)=y。我们就可以定义它的反函数 f − 1 f^{-1} f−1
- f − 1 f^{-1} f−1的定义域与 f f f的值域相同
- f − 1 f^{-1} f−1的值域与 f f f的定义域相同
- 如果 f ( x ) = y f(x)=y f(x)=y则 f − 1 ( y ) = x f^{-1}(y)=x f−1(y)=x
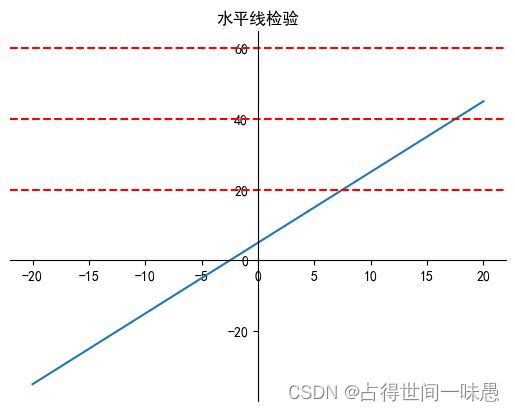
如何判断一个函数是否具有反函数呢?最简单的方法是通过函数的图像。反函数的要求是在值域中的任意y值都在定义域中有唯一确定的x值,满足 f ( x ) = y f(x)=y f(x)=y。它反应到图像中则是,在图像上绘制任意条水平线,每一条水平线至多与图像相交一次。这称为水平线检验。
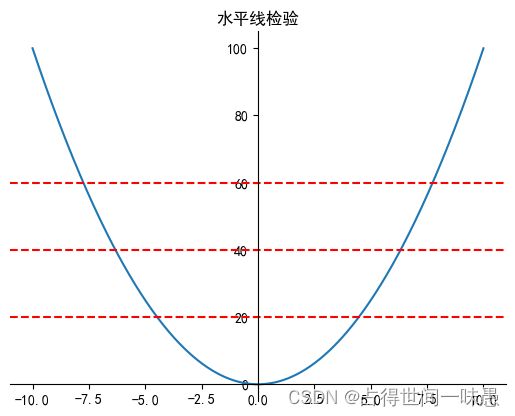
例如我们看一下 f ( x ) = 2 x + 5 f(x)=2x+5 f(x)=2x+5和 h ( x ) = x 2 h(x)=x^2 h(x)=x2的图像
f ( x ) f(x) f(x)的水平线检验的图像, f ( x ) f(x) f(x)具有反函数
h ( x ) h(x) h(x)的水平线检验的图像, h ( x ) h(x) h(x)不具有反函数
我们很容易从图像中看出谁具有反函数。
那么我们怎么求反函数呢?我们只需要写下 y = f ( x ) y=f(x) y=f(x),然后尝试求解出x就可以。
例如:求 f ( x ) = 2 x + 5 f(x)=2x+5 f(x)=2x+5的反函数 f − 1 f^{-1} f−1。我们写出 y = f ( x ) y=f(x) y=f(x)。将 f ( x ) f(x) f(x)带入,得到:
y = 2 x + 5 y − 5 = 2 x x = y − 5 2 y=2x+5\\ y-5=2x\\ x=\frac{y-5}{2} y=2x+5y−5=2xx=2y−5
所以 f − 1 ( y ) = y − 5 2 f_{-1}(y)=\frac{y-5}{2} f−1(y)=2y−5
1.4函数的复合
1.4.1 复合的定义
函数的复合是指将一个函数的输出作为另一个函数的输入。考虑函数 f ( x ) = l o g 2 ( x 2 ) f(x)=log_2{(x^2)} f(x)=log2(x2),我们可以将 x x x替换为任何使函数有意义的对象。如:用 g ( x ) = x + 3 g(x)=x+3 g(x)=x+3替换 x x x,得到 f ( g ( x ) ) = l o g 2 ( g ( x ) 2 ) f(g(x))=log_2{(g(x)^2)} f(g(x))=log2(g(x)2)。展开得到 f ( g ( x ) ) = l o g 2 ( ( x + 3 ) 2 ) f(g(x))=log_2{((x+3)^2)} f(g(x))=log2((x+3)2)。如果你需要将 f ( x ) f(x) f(x)写成 f ( 某表达式 ) f(某表达式) f(某表达式),只需要将每个 x x x都替换为表达式。
考虑函数 f ( x ) = ( x + 5 ) 2 f(x)=(x+5)^2 f(x)=(x+5)2,给定一个数x,我们计算 f ( x ) f(x) f(x)的步骤大致可以分为两步。第一步计算 x + 5 x+5 x+5,第二步计算 ( x + 5 ) (x+5) (x+5)的平方。因为我们可以将它分为按顺序执行的两个独立的计算。所以我们就可以将它们分别描述成一个函数。令 g ( x ) = x + 5 g(x)=x+5 g(x)=x+5, h ( x ) = x 2 h(x)=x^2 h(x)=x2。我们先将 x x x传递给函数 g g g进行 x + 5 x+5 x+5计算,得到 g ( x ) g(x) g(x),我们再将 g ( x ) g(x) g(x)传递给函数 h h h进行运算。最终的计算结果 h ( x ) h(x) h(x)就等于 f ( x ) f(x) f(x)。这个过程模拟了函数 f f f,这就是函数复合的过程。所以我们可以写出 f ( x ) = h ( g ( x ) ) f(x)=h(g(x)) f(x)=h(g(x)),也可以写作 f = h ∘ g f=h \circ g f=h∘g。 ∘ \circ ∘的意思是与…的复合。即函数 f f f是 g g g与 h h h的复合。
函数的复合是将一个函数的输出作为另一个函数的输入。这可以应用于多项式、指数、对数、分式、三角函数等多种类型的函数。
然而,乘法不适用于函数的复合,因为乘法满足交换律,即 a × b = b × a a \times b = b \times a a×b=b×a,这意味着乘法没有固定的计算顺序。因此,我们不能说一个乘法操作是由两个函数复合得到的。。
让我们来做几个练习题来巩固知识点吧。
若 z ( x ) = x + 5 z(x)=x+5 z(x)=x+5, g ( x ) = x 2 g(x)=x^2 g(x)=x2, h ( x ) = 2 x h(x)=2^x h(x)=2x,则函数 f = h ∘ g ∘ z f=h \circ g \circ z f=h∘g∘z的表达式是什么?我们从右边开始,将 z z z代换到g,再将结果代换到g:
f ( x ) = h ( g ( z ( x ) ) ) = h ( g ( x + 5 ) ) = h ( ( x + 5 ) 2 ) = 2 ( x + 5 ) 2 f(x)=h(g(z(x)))=h(g(x+5))=h((x+5)^2)=2^{(x+5)^2} f(x)=h(g(z(x)))=h(g(x+5))=h((x+5)2)=2(x+5)2
若 f ( x ) = 5 ( 2 x + 6 ) 3 f(x)=\frac{5}{\sqrt{(2x+6)^3}} f(x)=(2x+6)35,那怎么将函数 f f f分解成几个简单函数呢?让我们先找到 x x x,我们需要对x乘以2再加上6,所以设 g ( x ) = 2 x + 6 g(x)=2x+6 g(x)=2x+6。然后要对结果进行求立方运算,所以设 h ( x ) = x 3 h(x)=x^3 h(x)=x3。接的我们需要求平方根,所以设 j ( x ) = x j(x)=\sqrt{x} j(x)=x。最后需要取到数,并乘以5,设 k ( x ) = 5 x k(x)=\frac{5}{x} k(x)=x5。综上所述,我们可以得到
f ( x ) = k ( j ( h ( g ( x ) ) ) ) f(x)=k(j(h(g(x)))) f(x)=k(j(h(g(x))))
这并不是函数 f f f的唯一分解方式,大家还可以找出其他的分解方式吗?
1.4.2 求复合函数的定义域
若 g ( x ) = x 2 g(x)=x^2 g(x)=x2, y = f ( g ( x ) ) y=f(g(x)) y=f(g(x)),其中 x ∈ [ 0 , 5 ] x \in [0,5] x∈[0,5] , f ( x ) f(x) f(x)的定义域是多少?
求 f ( x ) f(x) f(x)的定义域就是求g(x)的值域。因为 g ( x ) = x 2 g(x)=x^2 g(x)=x2,并且 x x x的取值范围是 [ 0 , 5 ] [0,5] [0,5],所以 g ( x ) g(x) g(x)的值域(即 x 2 x^2 x2的可能值)是 [ 0 , 25 ] [0,25] [0,25]。这就是 f ( x ) f(x) f(x)的定义域。
若函数 f ( x ) f(x) f(x)的定义域为 [ 0 , 1 ] [0,1] [0,1],则函数 f ( s i n ( x ) ) f(sin(x)) f(sin(x))的定义域是什么?函数 f ( s i n ( x ) ) f(sin(x)) f(sin(x))是由 f ( x ) f(x) f(x)与 s i n ( x ) sin(x) sin(x)复合而来的,所以 s i n ( x ) sin(x) sin(x)的值域等于 f ( x ) f(x) f(x)的定义域。求函数 f ( s i n ( x ) ) f(sin(x)) f(sin(x))的定义域就是求当 s i n ( x ) sin(x) sin(x)的值域为 [ 0 , 1 ] [0,1] [0,1]时它的定义域。因此, f ( s i n ( x ) ) f(sin(x)) f(sin(x))的定义域是所有使得 s i n ( x ) sin(x) sin(x)的值在 [ 0 , 1 ] [0,1] [0,1]范围内的 x x x的集合。这对应于 x x x在每个 [ n π − π 2 , n π + π 2 ] [n\pi-\frac{\pi}{2}, n\pi+\frac{\pi}{2}] [nπ−2π,nπ+2π]区间内的值,其中 n n n是任何整数。
让我们来总结一下:
- 对于复合函数 f ( g ( x ) ) f(g(x)) f(g(x)), g ( x ) g(x) g(x)的值域应该是 f ( x ) f(x) f(x)的定义域的子集。反之亦然。 f ( x ) f(x) f(x)的定义域必须包含 g ( x ) g(x) g(x)的值域。
1.5 函数的奇偶性
函数的奇偶性描述的是函数的对称性。在图像上:如果一个函数是关于y轴对称,我们则称它为偶函数;如果函数是关于原点对称,则称为奇函数。
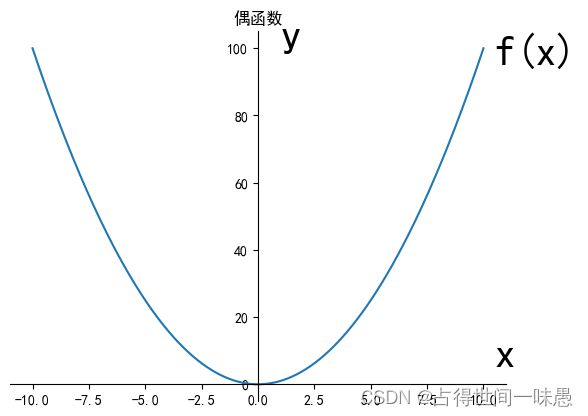
考虑函数 f ( x ) = x 2 f(x)=x^2 f(x)=x2,让我们画出它的图像:
我们很容易看出它是偶函数,因为它关于y轴对称。
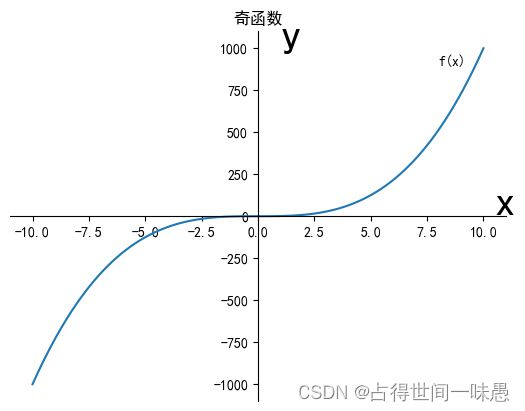
再来看函数 f ( x ) = x 3 f(x)=x^3 f(x)=x3,画出它的图像。
因为它关于原点对称,所以它是奇函数。
现在,让我们从代数角度来了解函数的奇偶性。
我们说一个函数关于y轴对称,那么这意味着 f ( − x ) = f ( x ) f(-x)=f(x) f(−x)=f(x)。这很容易可以从图像中看出。现在我们就可以用数学语言为偶函数下一个定义:
如果对于所有在函数定义域内的 x x x,都有 f ( − x ) = f ( x ) f(-x) = f(x) f(−x)=f(x),那么这个函数就被称为偶函数。
同样的,一个函数关于直线原点对称,那么意味着 f ( − x ) = − f ( x ) f(-x)=-f(x) f(−x)=−f(x)。现在我们就可以用数学语言为偶函数下一个定义:
*如果对于所有在函数定义域内的 x x x,都有 f ( − x ) = − f ( x ) f(-x) = -f(x) f(−x)=−f(x),那么这个函数就被称为奇函数。
一个函数可能是奇的,可能是偶的,也可能是非奇非偶的,大多数函数是非奇非偶的。只有一个函数是即奇又偶的,他就是对所有x成立的 f ( x ) = 0 f(x)=0 f(x)=0。
考虑函数 f ( x ) = l o g 10 2 x 4 − 3 x 2 f(x)=log_{10}{2x^4-3x^2} f(x)=log102x4−3x2,我们怎么判断它的奇偶性呢?方法很简单,只需要将每个 x x x替换成 − x -x −x,并计算 f ( − x ) f(-x) f(−x)。然后进行化简,如果得到 f ( x ) f(x) f(x)则说明是偶函数,得到 − f ( x ) -f(x) −f(x)则说明是奇函数。如果都不是则是非奇非偶的。
f ( − x ) = l o g 10 2 ( − x ) 4 − 3 ( − x ) 2 = l o g 10 2 x 4 − 3 x 2 = f ( x ) f(-x)=log_{10}{2(-x)^4-3(-x)^2}=log_{10}{2x^4-3x^2}=f(x) f(−x)=log102(−x)4−3(−x)2=log102x4−3x2=f(x)
因此 f ( x ) f(x) f(x)是偶函数。
若函数 g g g和 h h h均是奇函数,那么 f ( x ) = h ( x ) g ( x ) f(x)=h(x)g(x) f(x)=h(x)g(x)的奇偶性是什么呢?让我们从 f ( − x ) f(-x) f(−x)开始,我们有 f ( − x ) = h ( − x ) g ( − x ) f(-x)=h(-x)g(-x) f(−x)=h(−x)g(−x)。因为 g g g和 h h h均是奇函数,所以
f ( − x ) = ( − h ( x ) ) ( − g ( x ) ) = h ( x ) g ( x ) = f ( x ) f(-x)=(-h(x))(-g(x))=h(x)g(x)=f(x) f(−x)=(−h(x))(−g(x))=h(x)g(x)=f(x)
我们可以得到两个奇函数的乘积是偶函数。除此之外,我们还有,两个偶函数之积仍未偶函数,奇函数和偶函数之积是奇函数。大家可以尝试自己取证明它们。
1.6 函数的增减性
考虑函数 f ( x ) = 2 x + 5 f(x)=2x+5 f(x)=2x+5.画出它的图像
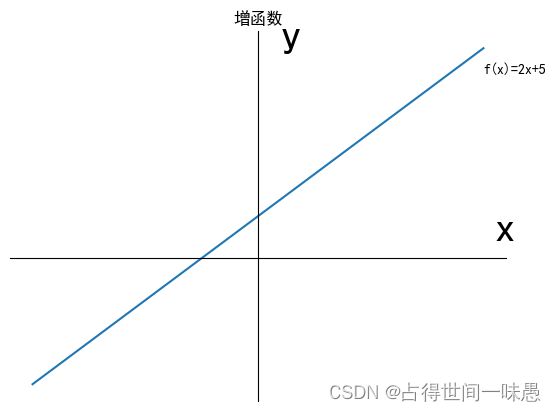
不难发现:对于函数定义域内所有的 x 1 < x 2 x_1
如果对于所有 x 1 < x 2 x_1
注释
集合
集合是由一些明确的或者不明确的元素所构成的,这些元素被称为集合的成员。
集合有两种表示方式:列举法和描述法。
- 列举法:直接列出集合中的元素,如:集合 A = { 1 , 2 , 3 } A=\{1,2,3\} A={1,2,3}
- 描述法:通过描述元素的性质来定义集合。如:集合 B = { x ∣ x > 0 , x ∈ R } B=\{x|x>0,x \in R\} B={x∣x>0,x∈R}。这个集合描述的是所有大于0的实数。其中 R R R表示的是所有实数的集合,而符号 ∈ \in ∈表示的是属于, x ∈ R x \in R x∈R 表示的就是 x属于R,换句话说,x是实数集中的一个元素。
子集
如果集合B中包含集合A的所有元素,我们则称集合A是集合B的一个子集。记作 A ⊆ B A \subseteq B A⊆B。
补集
我们一般将涉及到所有元素的集合称作全集U。而A相对于U的补集是指的在U中除去集合A中所有元素后剩余的元素构成的集合。记作 B = ∁ U A B=\complement_{U}A B=∁UA。其中B是A相对于U的补集。它满足下述关系
B = U − A B=U-A B=U−A
交集
交集C指的是集合A和集合B共有的那一部分元素组成的集合。记作 C = A ∩ B C=A \cap B C=A∩B
并集
并集C指的是集合A的所有元素加上集合B中所有元素构成的集合。记作 C = A ∪ B C=A\cup B C=A∪B。需要注意的是集合内的元素是具有不重复性的。
指数
这里对指数做一个简单的介绍,在后续的章节会具体讲解。
形如 a n a^n an的表达式称为指数,其中a是底数,n是指数。这个表达式表示的是a的n次方,即a乘以自己n次。
指数具有一些性质:
- 任何数的0次方都等于1(除了0的0次方,这在数学中是没有定义的)。
- 任何数的1次方等于它自身。
- 负指数表示的是对于底数取倒数,在乘以负指数的绝对值次方。即 a − n = 1 a n a^{-n}=\frac{1}{a^n} a−n=an1。
- 底数必须是大于0且不等于1的实数。
对数
形如 log a c \log_a c logac的表达式称为对数,其中 a a a称为底数, c c c称为真数。对数是对指数的逆运算。对数表示的是在以a为底的指数运算中,使得运算结果等于c的指数b。换句话说,如果 a b = c a^b=c ab=c,则 log a c = b \log_a c=b logac=b。
对数具有一些性质:
- log a 1 = 0 \log_a 1 = 0 loga1=0,因为任何数的0次方都等于1。
- log a a = 1 \log_a a = 1 logaa=1,因为任何数的1次方都等于它自己。
- log a a b = b \log_a a^b=b logaab=b。
- 因为对数是指数的逆运算,所有对数的底数也必须是大于0且不等于1的实数。
- 对数的真数必须大于0,因为任何大于0的数的指数运算的结果都是大于0的。
区间
区间表示的是一个由两个端点确定集合,这个集合是实数集的子集。它表示的是所有在某个范围内的实数。
[ a , b ] [a,b] [a,b] 表示的是所有大于等于a且小于等于b的实数的集合。这称为闭区间。
( a , b ) (a,b) (a,b) 表示示的是所有大于a且小于b的实数的集合。这称为开区间。
[ a , b ) [a,b) [a,b) 表示的是所有大于等于a且小于b的实数的集合。这称为左闭右开区间。
( a , b ] (a,b] (a,b] 表示的是所有大于a且小于等于b的实数的集合。这称为左开右闭区间。
( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞) 表示的是从负无穷到正无穷。如果一端是无穷,则这一端的括号均为小括号。这是因为无穷是取不到的。
+ ∞ +\infty +∞与 − ∞ -\infty −∞
∞ \infty ∞表示的是无穷(infinity),无穷是一个表示极限大或极限小的概念。在数学表达式中,无穷大通常表示为 “+∞”,无穷小表示为 “-∞”。无穷并不是真正的数,而是一种表示极限的符号。
通常情况下,正无穷可以省略加号,直接写作"∞"
若有问题,恳请指正
未完待续