相关系数—如何从本质上理解协方差和相关系数（一）？

---

前言

“只有真正理解数学了才能从本质上理解某种现象和问题”，这句话不断激励我去探索数学原理。

---

一、先从公式说起

相关系数在度娘上解释为：“相关系数是研究变量之间线性相关程度的量”，这里的重点是线性相关程度，其对应的公式为：

这里存在一个非常重要的性质：

这个性质也充分说明了两个变量之间的（X/Y）之间的线性相关关系。不管怎么两个变量如果存在高度相关关系（相关系数大于0.8），那么也能找到a和b的值使Y=aX+b，这也是非常关键的一点（但这里存在一个问题，对于一个非线性系统怎么办？？值得思考，下面会有稍微涉及），对于相关系数的公式，最重要的就是协方差。

二、非线性函数的变量和自变量之间的相关关系

先看一张图，不同函数之间X和Y之间的曲线以及对应的相关系数：

其实单从曲线上也可以看出有一定的线性相关关系，就是其趋势可以用一条直线描述，这只是简单的函数示例，对应的脚本：

% 验证相关系数；
clc
clear
close all
opengl software
%% Y=Ax+b  y=3x+2
x = [1,2,3,4,5,6,7,8,9,10];
% x = rand(1,10);
y1(1,:) = 3*x+2;
rxy1 = corrcoef(x,y1(1,:));
%% Y=Ax^2+b
y1(2,:) = 3*(x.^2)+2;
rxy2 = corrcoef(x,y1(2,:));
%% Y=A*log(x^2)+b
y1(3,:) = 3*log10(x.^2)+2;
rxy3 = corrcoef(x,y1(3,:));
%% Y=exp(x^2)+b
y1(4,:) = exp(-x)+2;
rxy4 = corrcoef(x,y1(4,:));
%% Y=Ax^3+b
y1(5,:) = 3*(x.^3)+2;
rxy5 = corrcoef(x,y1(5,:));
%%
Y = y1';
plot(Y)
xlim([0,10])
ylim([-100,2500])
legend("Y=Ax+b相关系数1","Y=Ax^2+b相关系数0.97","Y=A*log(x^2)+b相关系数0.95","Y=exp(x^2)+b相关系数-0.71" + ...
    "","Y=Ax^3+b相关系数0.92")
grid on

还有一个网友列出这样几个图如何通俗理解相关系数？这一次绝对懂了

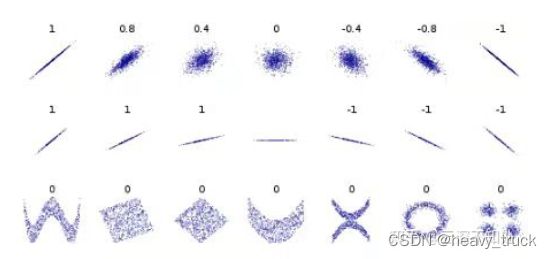
第三行相关系数为0，主要原因就是一个对称的数据。

三 、协方差

协方差在度娘上的解释为：“协方差表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。”读完之后并没有恍然大悟的感觉，反而有些一头雾水。
其实所谓协方差的本质，有些网友已经做相关分析，这里作为搬运工，链接如下：如何通俗地解释协方差，我们在看一下公式：

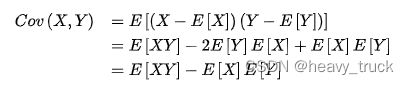
仅仅看第一行，完全和面积S=AB大致类比（期望就是考虑到概率论的知识），而对于均值，则可以认为把期望等于0，这个用途就比较广了，在对数据进行降维时也会用到这一概念，当然这是另一回事了。所以，协方差基本和面积类似，当然在真正计算协方差时，会排除一些奇异值（不是很恰当，当然不是不排除，而是乘以奇异值的概率，也就是把小概率事件缩小，把大概率事件放大，这一点很重要）。

四 、协方差公与系统

Y=AX+B的协方差推导公式：

与第1部分分母相除的结果为1；
此时考虑另一个问题，那就是对于非线性系统来说，存在y=hx这样的一个卷积乘的关系，这个x和y之间的相关系数改如何计算？其对应的公式就为：
cov（X,Y）=cov(X,hX)
如何解上述的方程，其实我们不用求解，而是用特例说明，对应脚本入下：

%% 卷积验证；
x = [1 0 1];
y1 = [1 0 1];
h = [.1 0.6 1];
y2 = conv(h,x);
y2 = y2(1:3);
rxy2 = corrcoef(x,y2);

此时，rxy2的值为4.8e-17，这就完全不相关了，当然不同的h值对应的结果是不一样 ，因此一个信号经过系统之后在和原始信号做相关函数分析时，就需要注意传递函数。
相关系数和系统的关系下一个博客分析。

---