【数学建模】《实战数学建模：例题与讲解》第八讲-回归分析（含Matlab代码）

本系列侧重于例题实战与讲解，希望能够在例题中理解相应技巧。文章开头相关基础知识只是进行简单回顾，读者可以搭配课本或其他博客了解相应章节，然后进入本文例题实战，效果更佳。

如果这篇文章对你有帮助，欢迎点赞与收藏~

回归分析基本概念

在当今数据驱动的研究与决策制定中，回归分析扮演着至关重要的角色。它是一种统计方法，用于研究和建模两组或多组变量之间的关系。在实际问题中，特别是当我们面临着大量相关的自变量（预测变量）和因变量（响应变量）时，选择合适的回归分析方法变得尤为重要。

经典多元线性回归（MLR）

多元线性回归是最基本且广泛使用的回归分析形式。它旨在使用多个预测变量来预测一个因变量。基于最小二乘准则，它通过最小化预测值和实际值之间的平方差来找到最佳拟合线。然而，当变量间存在多重共线性，或者自变量的数量远大于观测样本量时，多元线性回归的效果可能会受到限制。

主成分回归（PCR）

为了解决多元回归中的多重共线性问题，主成分回归（PCR）技术被提出。PCR先对自变量进行主成分分析（PCA），以减少变量间的共线性，并提取少量的主成分。然后，这些主成分被用作新的预测变量在回归分析中。这种方法有效降低了变量间的依赖性，但可能会丢失对原始变量的直接解释性。

偏最小二乘回归（PLS）

偏最小二乘回归是一种先进的多对多线性回归建模方法。它特别适用于自变量和因变量都很多、彼此间存在多重相关性，而样本量又相对较少的情况。PLS不仅考虑了自变量间的关系，还考虑了自变量与因变量间的关系。它通过寻找两组变量中共同变异的方向，可以在减少数据维度的同时，保留对响应变量有用的信息。

建模过程

PLS回归在建模时综合了主成分分析、典型相关分析和线性回归分析的特点。它不仅提供了一个合理的回归模型，而且还能进行类似于主成分分析和典型相关分析的探索，提供更丰富和深入的信息。

应用和优势

PLS回归在许多领域都有应用，特别是在化学计量学、生物信息学和社会科学中。它的优势在于能够处理高维数据集，解决多重共线性问题，并提供对复杂数据结构的深入理解。

偏最小二乘回归分析概述

偏最小二乘回归（PLS回归）分析是一种统计方法，它在多元统计分析中被用来建立因变量和自变量之间的线性关系模型。它是一种在因变量和自变量之间建立最大协方差的模型，尤其适合于变量个数多于观测数，或者变量之间存在多重共线性的情况。PLS回归不仅能够处理多维数据集，而且还能够在减少变量时保持模型的预测能力。

PLS回归的基本思想是将原始的自变量矩阵和因变量矩阵分别投影到新的空间，这些新空间的基是由原始变量的线性组合构成的。这些新空间的基被称为潜在变量或PLS成分。通过这种方式，PLS回归旨在找到少数几个潜在变量，这些潜在变量能够最好地解释自变量和因变量之间的关系。

PLS回归分析的步骤通常包括以下几个关键阶段：

1. 算法初始化：选择初始权重，开始迭代过程。
2. 权重向量的计算：计算自变量和因变量的权重向量，这些权重向量定义了原始变量到潜在变量空间的映射。
3. 潜在变量的提取：用权重向量提取自变量和因变量的得分，这些得分代表了潜在变量。
4. 内部关系的建立：在潜在变量空间内，建立自变量得分和因变量得分之间的回归模型。
5. 模型优化：通过交叉验证等方法确定潜在变量的最佳数目，以避免过拟合。
6. 参数估计：在确定了潜在变量数目后，用所有数据重新估计PLS回归模型的参数。
7. 模型评估：使用一些统计标准，如预测残差平方和（PRESS）和决定系数（R²），来评价模型的预测能力和解释能力。

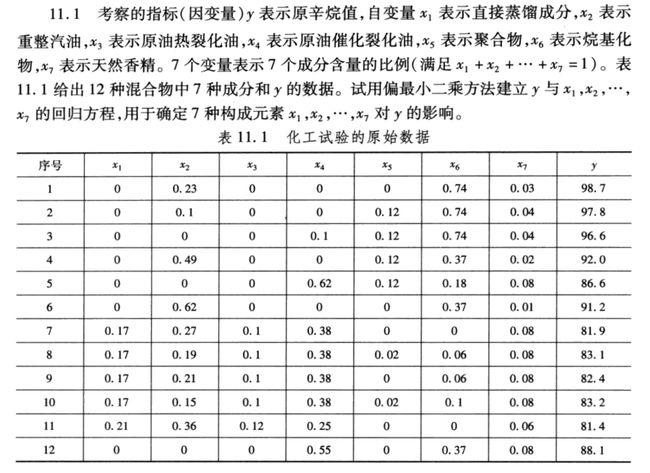
习题11.1

1. 题目要求

2.解题过程

解：

12个样本点分别用 i=1,…,12 表示各个样本点，自变量的观测数据矩阵即为$A=(a_{ij}{)}_{12\times 7}$，因变量的观测数据矩阵即为$B=[b_1,...,b_{12}{]}^T$。

（1）

数据标准化

将各指标值$a_{ij}$转换成标准化指标值$\widetilde{a_{ij}}$，即
$$\widetilde{a_{ij}}=\frac{a_{ij}-{\mu }_j^{(1)}}{s_j^{(1)}},i=1,2,...,12,j=1,...,7.$$
式中：
$$\begin{gathered} {\mu }_j^{(1)}=\frac{1}{12}\sum _{i=1}^{12}{a}_{ij}, \\ {s}_j^{(1)}=\sqrt{\frac{1}{12-1}\sum _{i=1}^{12}(a_{ij}-{\mu }_j^{(1)}{)}^2},(j=1,...,7), \end{gathered}$$
即${\mu }_j^{(1)}$、$s_j^{(1)}$为第j个自变量$x_j$的样本均值和样本标准差。对应地，称
$$\widetilde{x_j}=\frac{x_j-{\mu }_j^{(1)}}{s_j^{(1)}},j=1,...,7.$$
为标准化指标变量。

类似地，将$b_i$转换成标准化指标值$\widetilde{b_i}$，即
$$b_i=\frac{b_i-{\mu }^{(2)}}{s^{(2)}},i=1,2,...,12,$$
式中：
$$\begin{gathered} {\mu }^{(2)}=\frac{1}{12}\sum _{i=1}^{12}{b}_i \\ {s}^{(2)}=\sqrt{\frac{1}{12-1}\sum _{i=1}^{12}(b_i-{\mu }^{(2)}{)}^2} \end{gathered}$$
即${\mu }^{(2)},s^{(2)}$为因变量y的样本均值和样本标准差；

对应地，称
$$\tilde{y}=\frac{y-{\mu }^{(2)}}{s^{(2)}}$$
为对应的标准化变量。

（2）

分别提出自变量组和因变量组的成分。使用matlab求得7对成分，其中第一对成分为
$$\begin{array}{c}\{\begin{array}{ll}{\mu }_1& =-0.0906\widetilde{x_1}-0.0575{\tilde{x}}_2-0.0804{\tilde{x}}_3-0.116{\tilde{x}}_4+0.0238{\tilde{x}}_5-0.0657{\tilde{x}}_7,\\ v_1& =3.1874{\tilde{y}}_1.\end{array}\end{array}$$
前三个成分解释自变量的比率为91.83%，只要取3对成分即可。

（3）

求三个成分对标准化指标变量与成分变量之间的回归方程，求得自变量组和因变量组与$u_1、u_2、u_3$之间的回归方程分别为：

$${\tilde{x}}_1=-2.9991u_1-0.1186u_2+1.0472u_3,$$

$${\tilde{x}}_2=0.2095u_1-2.7981u_2+1.7237u_3,$$

…

$${\tilde{x}}_7=-2.7279u_1+1.3298u_2-1.3002u_3,$$

$${\tilde{y}}_1=3.1874u_1+0.7617u_2+0.3954u_3,$$

（4）

求因变量组与自变量组之间的回归方程

把（2）中成分$u_i$代入（3）中的回归方程，得到标准化指标变量的回归方程为：
$${\tilde{y}}_1=-0.1391{\tilde{x}}_1-0.2087{\tilde{x}}_2-0.1376{\tilde{x}}_3-0.2932{\tilde{x}}_4-0.0384{\tilde{x}}_5+0.4564{\tilde{x}}_6-0.1434{\tilde{x}}_7.$$
将标准化变量$\tilde{y},{\tilde{x}}_j,(j=1,...,7)$分别还原成原始变量$y,x_j$，就可以得到结果。

3.程序

求解的MATLAB程序如下：

clc, clear

% 导入数据
ab0 = [0, 0.23, 0, 0, 0, 0.74, 0.03, 98.7; ...
    0, 0.1, 0, 0, 0.12, 0.74, 0.04, 97.8; ...
    0, 0, 0, 0.1, 0.12, 0.74, 0.04, 96.6; ...
    0, 0.49, 0, 0, 0.12, 0.37, 0.02, 92.0; ...
    0, 0, 0, 0.62, 0.12, 0.18, 0.08, 86.6; ...
    0, 0.62, 0, 0, 0, 0.37, 0.01, 91.2; ...
    0.17, 0.27, 0.1, 0.38, 0, 0, 0.08, 81.9; ...
    0.17, 0.19, 0.1, 0.38, 0.02, 0.06, 0.08, 83.1; ...
    0.17, 0.21, 0.1, 0.38, 0, 0.06, 0.08, 82.4; ...
    0.17, 0.15, 0.1, 0.38, 0.02, 0.1, 0.08, 83.2; ...
    0.21, 0.36, 0.12, 0.25, 0, 0, 0.06, 81.4; ...
    0, 0, 0, 0.55, 0, 0.37, 0.08, 88.1];
% 均值和方差
mu = mean(ab0);
sig = std(ab0);
% 标准化以后的自变量和因变量数据
ab = zscore(ab0);
a = ab(:, [1 : 7]);
b = ab(:, [8: end]);

% 主成分的个数3
[XL, YL, XS, YS, BETA, PCTVAR, MSE, stats] = plsregress(a, b, 3);

n = size(a, 2);
m = size(b, 2);

format long g
BETA2(1, :) = mu(n + 1 : end) - mu(1:n) ./ sig(1:n) * BETA([2 : end], :) .* sig(n + 1 :end);
BETA2([2: n + 1], :) = (1 ./ sig(1:n))' * sig(n + 1 : end) .* BETA([2: end], :)

%直方图
bar(BETA','k');

4.结果

所以，最终建立的回归方程如下：
$$\begin{array}{rl}y& =92.6759894798203-9.82831779652421\times x_1-6.96018146108128\times x_2-16.6662390524996\times x_3\\ & -8.4218024072797\times x_4-4.38893380525098\times x_5+10.1613044805558\times x_6\\ & -34.5289588223774\times x_7\end{array}$$

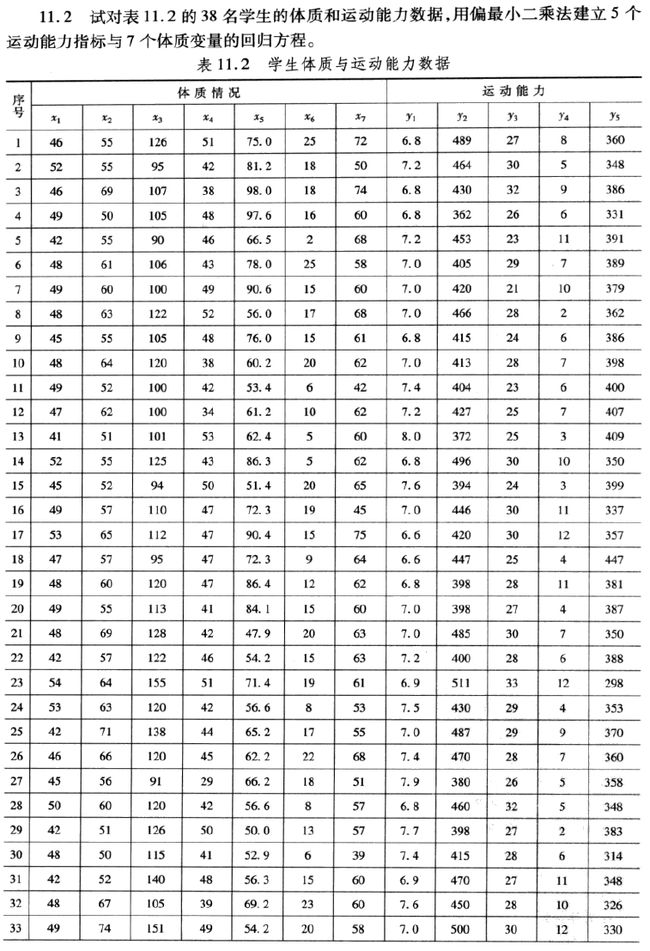
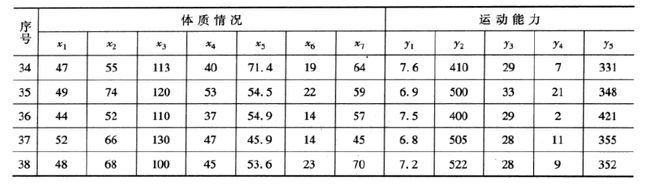
习题11.2

1. 题目要求

2.解题过程

解：

解题思路与方法与上一题类似，本题不再详细赘述。

不同点在于，本题一共有5对成分。

3.程序

求解的MATLAB程序如下：

clc, clear

% 导入数据
ab0 = [46, 55, 126, 51, 75.0, 25, 72, 6.8, 489, 27, 8, 360; ...
    52, 55, 95, 42, 81.2, 18, 50, 7.2, 464, 30, 5, 348; ...
    46, 69, 107, 38, 98.0, 18, 74, 6.8, 430, 32, 9, 386; ...
    49, 50, 105, 48, 97.6, 16, 60, 6.8, 362, 26, 6, 331; ...
    42, 55, 90, 46, 66.5, 2, 68, 7.2, 453, 23, 11, 391; ...
    48, 61, 106, 43, 78.0, 25, 58, 7.0, 405, 29, 7, 389; ...
    49, 60, 100, 49, 90.6, 15, 60, 7.0, 420, 21, 10, 379; ...
    48, 63, 122, 52, 56.0, 17, 68, 7.0, 466, 28, 2, 362; ...
    45, 55, 105, 48, 76.0, 15, 61, 6.8, 415, 24, 6, 386; ...
    48, 64, 120, 38, 60.2, 20, 62, 7.0, 413, 28, 7, 398; ...
    49, 52, 100, 42, 53.4, 6, 42, 7.4, 404, 23, 6, 400; ...
    47, 62, 100, 34, 61.2, 10, 62, 7.2, 427, 25, 7, 407; ...
    41, 51, 101, 53, 62.4, 5, 60, 8.0, 372, 25, 3, 409; ...
    52, 55, 125, 43, 86.3, 5, 62, 6.8, 496, 30, 10, 350; ...
    45, 52, 94, 50, 51.4, 20, 65, 7.6, 394, 24, 3, 399; ...
    49, 57, 110, 47, 72.3, 19, 45, 7.0, 446, 30, 11, 337; ...
    53, 65, 112, 47, 90.4, 15, 75, 6.6, 420, 30, 12, 357; ...
    47, 57, 95, 47, 72.3, 9, 64, 6.6, 447, 25, 4, 447; ...
    48, 60, 120, 47, 86.4, 12, 62, 6.8, 398, 28, 11, 381; ...
    49, 55, 113, 41, 84.1, 15, 60, 7.0, 398, 27, 4, 387; ...
    48, 69, 128, 42, 47.9, 20, 63, 7.0, 485, 30, 7, 350; ...
    42, 57, 122, 46, 54.2, 15, 63, 7.2, 400, 28, 6, 388; ...
    54, 64, 155, 51, 71.4, 19, 61, 6.9, 511, 33, 12, 298; ...
    53, 63, 120, 42, 56.6, 8, 53, 7.5, 430, 29, 4, 353; ...
    42, 71, 138, 44, 65.2, 17, 55, 7.0, 487, 29, 9, 370; ...
    46, 66, 120, 45, 62.2, 22, 68, 7.4, 470, 28, 7, 360; ...
    45, 56, 91, 29, 66.2, 18, 51, 7.9, 380, 26, 5, 358; ...
    50, 60, 120, 42, 56.6, 8, 57, 6.8, 460, 32, 5, 348; ...
    42, 51, 126, 50, 50.0, 13, 57, 7.7, 398, 27, 2, 383; ...
    48, 50, 115, 41, 52.9, 6, 39, 7.4, 415, 28, 6, 314; ...
    42, 52, 140, 48, 56.3, 15, 60, 6.9, 470, 27, 11, 348; ...
    48, 67, 105, 39, 69.2, 23, 60, 7.6, 450, 28, 10, 326; ...
    49, 74, 151, 49, 54.2, 20, 58, 7.0, 500, 30, 12, 330; ...
    47, 55, 113, 40, 71.4, 19, 64, 7.6, 410, 29, 7, 331; ...
    49, 74, 120, 53, 54.5, 22, 59, 6.9, 500, 33, 21, 348; ...
    44, 52, 110, 37, 54.9, 14, 57, 7.5, 400, 29, 2, 421; ...
    52, 66, 130, 47, 45.9, 14, 45, 6.8, 505, 28, 11, 355; ...
    48, 68, 100, 45, 53.6, 23, 70, 7.2, 522, 28, 9, 352];

% 均值和方差
mu = mean(ab0);
sig = std(ab0);
% 标准化以后的自变量和因变量数据
ab = zscore(ab0);
a = ab(:, [1 : 7]);
b = ab(:, [8: end]);

% 主成分个数5
[XL, YL, XS, YS, BETA, PCTVAR, MSE, stats] = plsregress(a, b, 5);

n = size(a, 2);
m = size(b, 2);

format long g
BETA2(1, :) = mu(n + 1 : end) - mu(1:n) ./ sig(1:n) * BETA([2 : end], :) .* sig(n + 1 :end);
BETA2([2: n + 1], :) = (1 ./ sig(1:n))' * sig(n + 1 : end) .* BETA([2: end], :)

%直方图
bar(BETA', 'k');

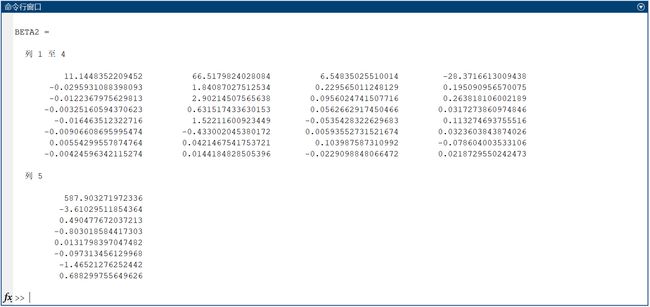
4.结果

所以，最终建立的回归方程如下：
$$\begin{array}{rl}{y}_1& =11.1448352209452-0.0295931088398093\times x_1-0.0122367975629813\times x_2-0.00325160594370623\times x_3\\ & -0.016463512322716\times x_4-0.00906608695995474\times x_5+0.00554299557874764\times x_6\\ & -0.00424596342115274\times x_7\\ y_2& =66.5179824028084+1.84087027512534\times x_1+2.90214507565638\times x_2+0.631517433630153\times x_3\\ & +1.52211600923449\times x_4-0.433002045380172\times x_5+0.0421467541753721\times x_6\\ & +0.0144184828505396\times x_7\\ y_3& =6.54835025510014+0.229565011248129\times x_1+0.0956024741507716\times x_2+0.0562662917450466\times x_3\\ & -0.0535428322629683\times x_4+0.00593552731521674\times x_5+0.103987587310992\times x_6\\ & -0.0229098848066472\times x_7\\ y_4& =-28.3716613009438+0.195090956570075\times x_1+0.263818106002189\times x_2+0.0317273860974846\times x_3\\ & +0.113274693755516\times x_4+0.0323603843874026\times x_5-0.078604003533106\times x_6\\ & +0.0218729550242473\times x_7\\ y_5& =587.903271972336-3.61029511854364\times x_1+0.490477672037213\times x_2-0.803018584417303\times x_3\\ & +0.0131798397047482\times x_4-0.097313456129968\times x_5-1.46521276252442\times x_6\\ & +0.688299755649626\times x_7\end{array}$$

如果这篇文章对你有帮助，欢迎点赞与收藏~