汉诺塔（函数递归）

前言
汉诺塔问题是一个经典的数学谜题，也是函数递归的一个经典问题，起源于印度。问题的设定是有三个柱子，第一个柱子上有一组不同大小的圆盘，按照从上到下依次变大的顺序摆放。目标是将所有的圆盘从第一个柱子移动到第三个柱子上，但是在移动过程中必须遵守以下规则：
1，每次只能移动一个圆盘。
2，每次移动时，只能将一个圆盘从柱子的顶端移到另一个柱子的顶端。
3，不允许将大圆盘放在小圆盘的上面。
在了解了规则之后我们该怎么样用函数递归的方式解决它呢？那么话不多说我们现在开始。

函数递归讲究一种由大化小的思想。
首先我们要定义一个函数hanoi（int n,char pos1 ,char pos2 ,char pos3）
首先n代表有n个盘子，pos1是起始位置，pos2是中转位置，pos3是目的位置。
然后我们在定义一个move函数move（char pos1，char pos2）将pos1的盘子移动到pos2上我们先写一下简单的move函数

void move(char pos1, char pos2)
{
	printf("%c -> %c ", pos1, pos2);
}

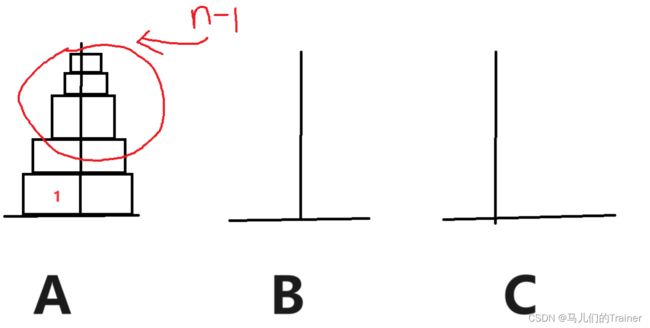
如图分别有三个柱子a,b,c，我们的目的是将a上的n个盘子移动到c上。当n=1时我们可以直接将盘子从a移到c。所以我们先这样写。

void hanoi(int n, char pos1, char pos2, char pos3)
{
	if (n == 1)
	{
		move(pos1, pos3);
	}
	else
	{
	
	}
}

当n不等于1时，我们的主要思想是现将a上的n-1个盘子移动到b上，然后将a上剩余的一个盘子移动到c上。如图。

那么此时我们要把n-1个盘子从a移动到b，即起始位置是a，目的位置自然是b，那c就是我们的中转位置。那么我们开始写代码。

void hanoi(int n, char pos1, char pos2, char pos3)
{
	if (n == 1)
	{
		move(pos1, pos3);
	}
	else
	{
	hanoi(n-1,pos1,pos3,pos2);//此时pos2是目的位置，pos1是起始位置
	move（pos1,pos3）;//将a上的那一个放到c上
	}
}

接下来我们需要把b上的n-1个放到c上，此时我们的b就是起始位置，c是目的位置，而a就是中转位置。如图所示。

到这里我们发现就完成了任务那么我们再写一下代码。

void hanoi(int n, char pos1, char pos2, char pos3)
{
	if (n == 1)
	{
		move(pos1, pos3);
	}
	else
	{
	hanoi(n-1,pos1,pos3,pos2);//此时pos2是目的位置，pos1是起始位置
	move（pos1,pos3）;//将a上的那一个放到c上
	hanoi(n-1,pos2,pos1,pos3);//此时pos2是起始位置，pos3是目的位置
	}
}

这样我们的hanoi函数就写好了下面我们来演示。

#include
void move(char x, char y)
{
	printf("%c -> %c ", x, y);
}
void hanoi(int n, char pos1, char pos2, char pos3)
{
	if (n == 1)
	{
		move(pos1, pos3);
	}
	else
	{
		hanoi(n - 1, pos1, pos3, pos2);//此时pos2是目的位置，pos1是起始位置
		move(pos1, pos3);//将a上的那一个放到c上
		hanoi(n - 1, pos2, pos1, pos3);//此时pos2是起始位置，pos3是目的位置
	}
}
int main()
{
	int n;
	scanf("%d", &n);//输入共有n个盘子
	char a = 'A', b = 'B', c = 'C';
	hanoi(n,a,b,c);
	return 0;
}

输入n=4时结果是这样的

尾声
关于函数递归经典问题汉诺塔的分享就到这里，如果觉得博主讲的不错请给博主一个赞和收藏鼓励一下博主，关注博主不迷路，我们下期再见！