(图解)单链表删除结点值为x的结点算法
目录
一、非递归的算法
第一种算法思路如下:
第二种算法思路如下:
二、递归的算法
一、非递归的算法
第一种算法思路如下:
- 先判断链表L是否为空,空链表退出程序;
- 用p利用while循环从头到尾扫描单链表,pre指向 *p 结点的前驱;
- 在while循环中,用 if 语句判断是结点是否是要删除的结点,是的话就删除此结点并且pre->next指向p结点的后驱,否则让pre、p指向同步后移个结点。
时间复杂度:O(n) 空间复杂度:O(1)
// 单链表的结点存储结构
typedef struct LNode{
ElemType data; // 数据域
struct LNode *next; // 结点域
} LNode, *LinkList;算法实现:
void Del_x(LinkList L, ElemType x){
// L为带头结点的链表
LinkList p = L->next, pre = L, q;
if (p == NULL)
{
printf("链表为空!\n");
return;
}
while(p){
if (p->data == x) {
q = p; // q指向要删除的结点
p = p->next; // p->指向要删除结点的后驱
pre->next = p; // q的前驱指向q的后驱
free(q); // 释放q(需要删除的结点)
}
else{
pre = p; // pre向下后移
p = p->next; // p与pre同步向后移,这两步不能调换顺序
}
}
return;
}图解算法:
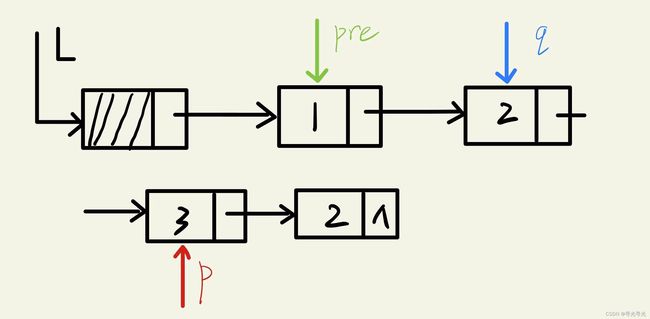
先看下面这个链表,咱们要删除 x = 2 的结点
L指向头结点
pre开始指向头结点,p指向链表的第一个结点,通过while循环中的 if 语句判断,p->data ![]() 2,故pre和q同步后移。
2,故pre和q同步后移。
后移后p->data = 2,因此要删除这个结点,即指行while循环里面的 if 语句,q指向要删除的结点,
p指向要删除结点的后驱,pre不要移动。
然后通过free()函数将 q 指向的空间释放,并且pre的后驱指向 p(即pre->next = p),此时链表没有 q指向的结点。
然后再通过 if 语句判断,p->data ![]() 2,pre 和 q 同步后移。
2,pre 和 q 同步后移。
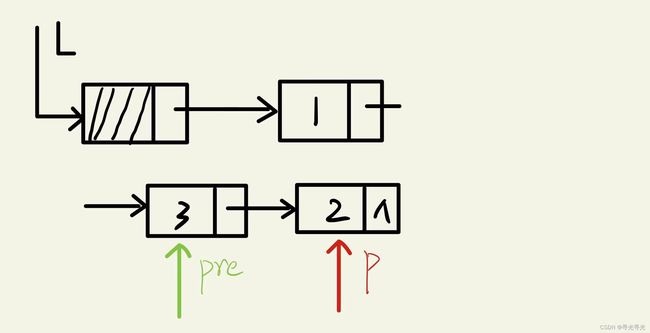
然后p->data = 2即要删除这个结点,p的后驱是空指针NULL,故最后 p = NULL,通过free()函数释放此结点,然后pre的后驱指向 p,即 pre->next = NULL。
然后p = NULL,循环结束,链表中无结点数据域等于2的结点,任务完成。
第二种算法思路如下:
- 利用尾插法建立单链表;
- p用来扫描L的所有结点,当其值不为x时,将其链接到L之后,否则将其释放。
时间复杂度:O(n) 空间复杂度:O(1)
算法实现:
void Del_x(LinkList L, ElemType x){
LinkList p = L->next, r = L, q;
if ( p == NULL)
{
printf("链表为空!\n");
return;
}
while(p){
if (p->data != x){
r->next = p; // p结点的值不为x,链接到L的尾部
r = p; // 方便下次链接
p = p->next;
}
else{
q = p; // 保存要删除的结点
p = p->next; // 指向要删除结点的后驱,继续扫描
free(q); // 释放结点
}
}
r->next = NULL; // 插入结束后,尾结点的next域为NULL
return;
}图解算法:
这个算法咱们可以这么理解,类似创建了新链表(在原链表上创建),然后往新链表插入结点的值不为x的结点,用的内存还是原来结点的内存(即指向的内存和原结点的地址一致),并不是新的分配的内存。和实际创建新链表(不在原链表上创建),通过复制结点后插入不同,复制插入的结点的地址不是原结点的地址(即指向的内存地址与原结点不一致),而是新分配的内存。
先看这个链表的初始情况
咱们为了更好的理解,可以将这个链表分为两个链表,一个为L指向头结点的链表,一个为p指向除头结点所有结点组成的链表 。
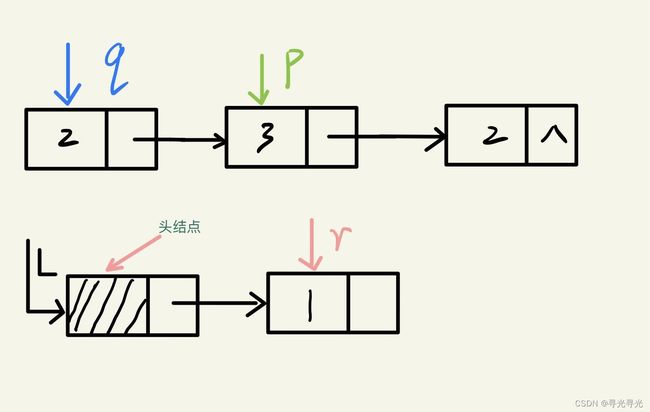
根据while循环的的 if 语句判断,p所指向的结点并不是要删除的结点,故p指向下一个节点,而刚才p指向的结点被链接到L所指向的链表上。
r->next = p; // p结点的值不为x,链接到L的尾部现在p指向的是要删除的结点,执行 if 语句的else部分,用q指向它,而p指向要删除结点的后驱。
然后通过free()函数释放q所指向的结点。
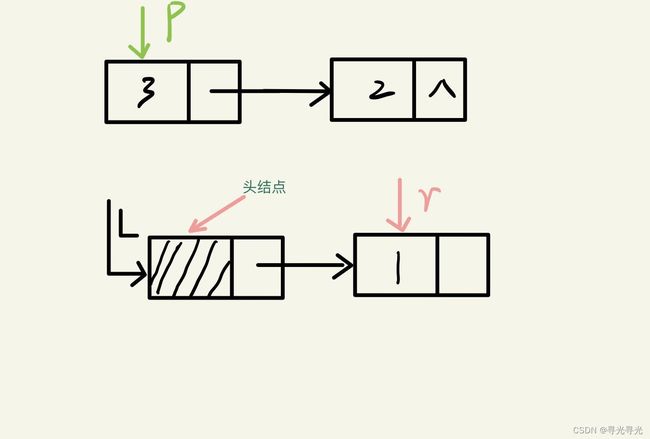
此时p指向的结点不是要删除的结点,p后移,p之前的结点链接到L指向的链表。
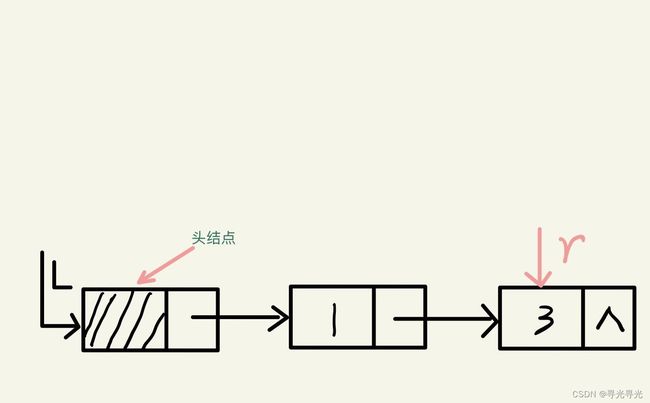
r->next = p; // p结点的值不为x,链接到L的尾部此时p指向的是要删除的结点,p向后移,并且q指向此结点。
通过free()函数释放q结点,此时p指向NULL,while循环结束,将L指向的链表最后结点的next指向NULL。
总结来说,就是把结点不是删除结点,就链接到L指向的链表,是要删除的结点通过free()函数释放。
二、递归的算法
算法思路如下:
- 找到基线条件(就是递归中止的条件),即链表为空,
- 找到递归条件,即每次递归离空链表更进一点
- 所以若链表L为空,递归函数 Del_x(L,x)什么也不做
- 若L->data = x, f(L,x)删除结点L,并且执行函数 Del_x(L->next, x),进行下次递归。
- 若L->data
 x,执行函数 Del_x(L->next, x),进行下次递归。
x,执行函数 Del_x(L->next, x),进行下次递归。
算法实现:
1、C++代码实现
// C++代码 LinkList &L,是一个引用
void Del_x(LinkList &L, ElemType x){
// L是不带头结点的链表
LinkList p;
if (L == NULL) // 递归出口
return;
if (L->data == x){
p = L; // 删除L,并让L指向下一个结点
L = L->next;
free(p);
Del_x(L, x); // 递归调用
}
else // 若L指向的结点不为x
Del_x(L->next, x); // 递归调用
return;
}
2、C语言代码实现
void Del_x(LinkList* head, ElemType x)
{
// head为指向不带头结点链表的第一个结点的指针的指针
// head为二级指针,需要修改内存上保存的指向LinkList的地址
LinkList p; // 保存要删除的结点地址
if (*head == NULL)
return; // 空链表,退出程序
if ((*head)->data == x) // 判断结点的值是否为x
{
p = *head; // 保存要删除的结点
*head = p->next; // 保存要删除的结点后驱地址
Del_x(head, x); // 递归函数
}
else
{
head = &((*head)->next); // 指向下一个结点的地址的地址
Del_x(head, x);
}
}这个算法要区分结构体指针和指向结构体指针的指针,可以看看我写的博客来了解结构体指针和指向结构体指针的区别。
结构体指针与指向结构体指针的区别
算法需要一个递归工作栈,深度为O(n),时间复杂度为O(n)。
测试程序:
#include
#include
#include
#define FLAG -1
typedef int ElemType;
typedef struct Node
{
ElemType data;
struct Node* next;
}LinkNode, * LinkList;
LinkList AddHead2(int flag);
void ShowLinkList(LinkList head);
int ListLength(LinkList head);
bool Insert(LinkList head, ElemType x, int i, int ListLength);
bool Delete(LinkList head, int i, int ListLength);
int ShowMeanu();
//void Del_x(ElemType x, LinkList head);
void Del_x(LinkList* head, ElemType x);
int main(void)
{
int choice;
LinkList head = (LinkList)malloc(sizeof(LinkNode));
head->next = NULL;
while (true)
{
choice = ShowMeanu();
switch (choice)
{
case 0: exit(0);
break;
case 1: head = AddHead2(FLAG);
break;
case 2: ShowLinkList(head);
break;
case 3: {
int i, x;
printf("请输入你要插入结点的位置:");
scanf("%d", &i);
printf("请输入你要插入结点的数据域的值:");
scanf("%d", &x);
int length = ListLength(head);
Insert(head, x, i, length);
}
break;
case 4: {
int i;
printf("请输入你要插入结点的位置:");
scanf("%d", &i);
Delete(head, i, ListLength(head));
}
break;
case 5: {
int length;
length = ListLength(head);
printf("链表的长度为:%d\n");
}
break;
case 6: {
int x;
printf("请输入要删除所有结点为x的值:");
scanf("%d", &x);
LinkList p = &(head->next);
//Del_x(head, x);
Del_x(p, x);
}
break;
default: printf("请输入恰当的值!!!!\n");
}
}
return 0;
}
int ShowMeanu()
{
int choice;
printf("欢迎来到链表测试功能!!!!!!\n");
printf("1.创建单链表 2.显示单链表中的结点\n");
printf("3.在链表i位置插入节点 4.删除链表第i个结点\n");
printf("5.单链表的表长 6.删除链表为x的所有结点\n");
printf("0.退出程序\n");
printf("请输入你想测试的功能序号:");
scanf("%d", &choice);
return choice;
}
LinkList AddHead2(int flag)
{
printf(" 输入 -1 停止创建单链表\n");
LinkList head, p, q;
head = (LinkList)malloc(sizeof(LinkNode));
head->next = NULL;
p = head;
ElemType x;
scanf("%d", &x);
while (x != flag)
{
q = (LinkList)malloc(sizeof(LinkNode));
q->data = x;
if (head->next == NULL)
head->next = q;
else
p->next = q;
p = q;
scanf("%d", &x);
}
if (p != NULL)
p->next = NULL;
return head;
}
void ShowLinkList(LinkList head)
{
LinkList p = head->next;
while (p != NULL)
{
printf("%d", p->data);
p = p->next;
}
printf("\n");
}
int ListLength(LinkList head)
{
int len = 0;
LinkList p = head;
while (p->next != NULL)
{
len++;
p = p->next;
}
return len;
}
bool Insert(LinkList head, ElemType x, int i, int ListLength)
{
LinkList p = head;
if (i > ListLength || p->next == NULL)
return false;
while (--i)
p = p->next;
LinkList q = (LinkList)malloc(sizeof(LinkNode));
q->data = x;
q->next = p->next;
p->next = q;
return true;
}
bool Delete(LinkList head, int i, int ListLength)
{
LinkList p = head;
if (i > ListLength || p->next == NULL)
return false;
while (--i)
p = p->next;
LinkList q = p->next;
p->next = q->next;
free(q);
return false;
}
/*void Del_x(ElemType x, LinkList head)
{
LinkList p = head->next, pre = head, q;
if (p == NULL)
{
printf("链表为空\n");
return;
}
while (p)
{
if (p->data == x)
{
q = p;
p = q->next;
pre->next = p;
free(q);
}
else
{
pre = p;
p = p->next;
}
}
return;
}*/
/*void Del_x(ElemType x, LinkList L) {
LinkList p = L->next, r = L, q;
if (p == NULL)
{
printf("链表为空!\n");
return;
}
while (p) {
if (p->data != x) {
r->next = p; // p结点的值不为x,链接到L的尾部
r = p; // 方便下次链接
p = p->next;
}
else {
q = p; // 保存要删除的结点
p = p->next; // 指向要删除结点的后驱,继续扫描
free(q); // 释放结点
}
}
r->next = NULL; // 插入结束后,尾结点的next域为NULL
return;
}*/
void Del_x(LinkList* head, ElemType x)
{
LinkList p;
if (*head == NULL)
return;
if ((*head)->data == x)
{
p = *head;
*head = p->next;
Del_x(head, x);
}
else
{
head = &((*head)->next);
Del_x(head, x);
}
}