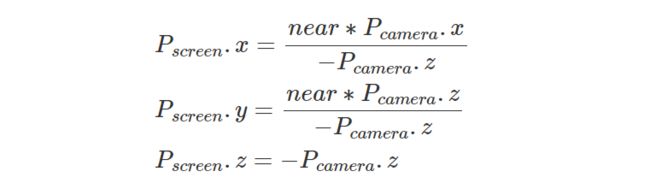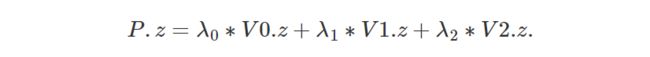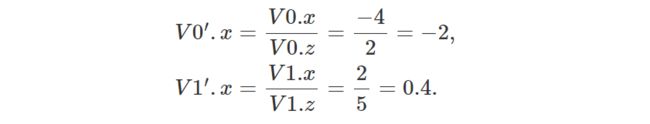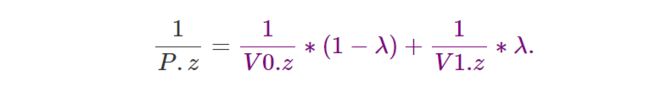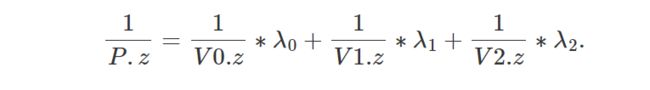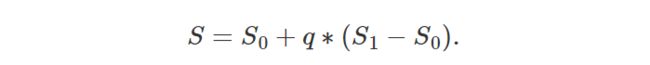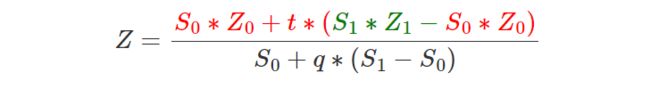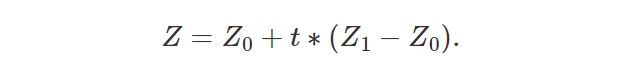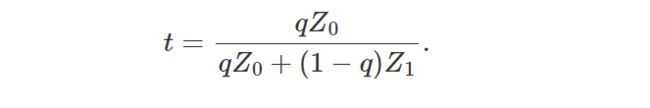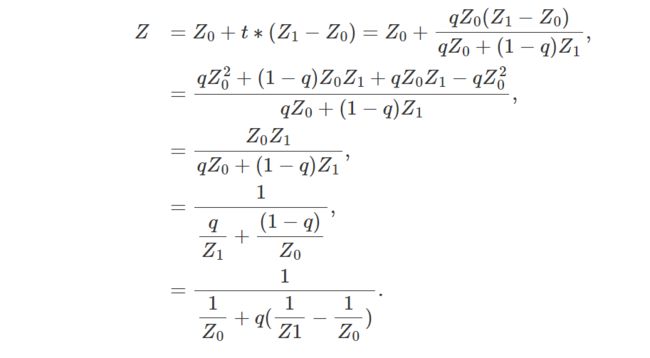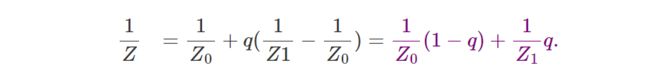光栅化渲染:可见性问题和深度缓冲区算法
在前面第二章中,我们了解到,在投影点(屏幕空间中的点)的第三个坐标中,我们存储原始顶点 z 坐标(相机空间中点的 z 坐标):
当一个像素与多个三角形重叠时,查找三角形表面上一点的 z 坐标非常有用。 我们找到 z 坐标的方法是使用我们在上一章中学到的重心坐标对原始顶点 z 坐标进行插值。 换句话说,我们可以将三角形顶点的 z 坐标视为任何其他顶点属性,并以与上一章中插值颜色相同的方式对它们进行插值。 在详细研究如何计算 z 坐标之前,让我们先解释一下为什么需要这样做。
NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎
1、深度缓冲或 Z 缓冲算法和隐藏面剔除
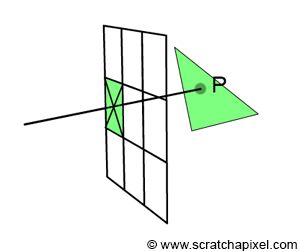
当一个像素与一个点重叠时,我们通过该像素看到的是三角形表面上的一小块区域,为了简化,我们将其简化为单个点(在图 1 中表示为 P):
图1:当一个像素与一个三角形重叠时,这个像素对应于三角形表面上的一个点(图中记为P)
因此,覆盖三角形的每个像素对应于该三角形表面上的一个点。 当然,如果一个像素覆盖多个三角形,那么我们就有几个这样的点。 发生这种情况时的问题是找到这些点中哪一个是可见的。 我们在图 2 中以 2D 形式说明了这个概念:
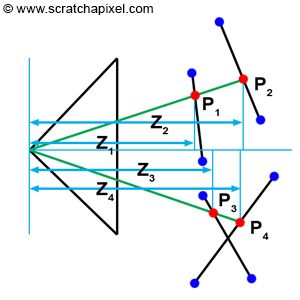
图 2:当一个像素与多个三角形重叠时,我们可以使用三角形 z 坐标上的点来找到这些三角形中哪一个距离相机最近
我们可以从后到前测试三角形(此技术需要首先通过减小深度对三角形进行排序),但当三角形彼此相交时,这并不总是有效(图 2,底部)。 唯一可靠的解决方案是计算像素重叠的每个三角形的深度,然后比较这些深度值以找出哪一个最接近相机。
如果查看图 2,你可以看到图像中的一个像素与 P1 和 P2 中的两个三角形重叠。 然而,P1 z 坐标 (Z1) 低于 P2 z 坐标 (Z2),因此我们可以推断 P1 在 P2 之前。 请注意,需要此技术,因为三角形是按“随机”顺序测试的。 正如之前提到的,我们可以按深度递减的顺序对三角形进行排序,但这还不够好。 一般来说,它们只是按照程序中指定的顺序进行测试,因此可以先测试离相机较近的三角形T1,然后再测试较远的三角形T2。 如果我们不比较这些三角形的深度,那么在这种情况下我们最终会看到最后测试的三角形 (T2),而实际上我们应该看到 T1。 正如之前多次提到的,这称为可见性(visibility)问题或隐藏面(hidden surface)问题。 对对象进行排序以便正确绘制对象的算法称为可见表面算法或隐藏面去除算法。 我们接下来要研究的深度缓冲区(depth buffer)或z缓冲区(z-buffer)算法就属于此类算法。
可见性问题的一种解决方案是使用深度缓冲区或 z 缓冲区。 深度缓冲区只不过是一个二维浮点数组,其尺寸与帧缓冲区相同,用于在三角形被光栅化时存储对象的深度。 创建此数组时,我们用一个非常大的数字初始化数组中的每个像素。 如果我们发现某个像素与当前三角形重叠,我们会执行以下操作:
- 我们首先计算像素重叠的三角形上的点的 z 坐标或深度。
- 然后,我们将当前三角形深度与该像素的深度缓冲区中存储的值进行比较。
- 如果我们发现深度缓冲区中存储的值大于三角形上点的深度,则新点比深度缓冲区中该像素位置处存储的点更靠近观察者或相机。 然后,深度缓冲区中存储的值将替换为新的深度,并且帧缓冲区将更新为当前的三角形颜色。 另一方面,如果深度缓冲区中存储的值小于当前深度样本,则像素重叠的三角形将被深度缓冲区中当前存储的深度的对象隐藏。
请注意,一旦处理完所有三角形,深度缓冲区就会包含“某种”图像,它表示场景中对象的可见部分与相机之间的“距离”(这不是距离,而是 z- 通过相机可见的每个点的坐标)。 深度缓冲区本质上对于解决可见性问题很有用,但是,它也可以在后处理中用于执行诸如 2D 景深、添加雾等操作。所有这些效果在 3D 中效果更好,但在 2D 通常更快,但结果并不总是像 3D 那样准确。
以下是深度缓冲区算法的伪代码实现:
float *depthBuffer = new float [imageWidth * imageHeight];
// Initialize depth-buffer with a very large number
for (uint32_t y = 0; y < imageHeight; ++y)
for (uint32_t x = 0; x < imageWidth; ++x)
depthBuffer[y][x] = INFINITY;
for (each triangle in the scene) {
// Project triangle vertices
...
// Compute 2D triangle bounding-box
...
for (uint32_t y = bbox.min.y; y <= bbox.max.y; ++y) {
for (uint32_t x = bbox.min.x; x <= bbox.max.x; ++x) {
if (pixelOverlapsTriangle(i + 0.5, j + 0.5) {
// Compute the z-coordinate of the point on the triangle surface
float z = computeDepth(...);
// Current point is closest than object stored in depth/frame-buffer
if (z < depthBuffer[y][x]) {
// Update depth-buffer with that depth
depthBuffer[y][x] = z;
frameBuffer[y][x] = triangleColor;
}
}
}
}
}2、通过插值求 Z
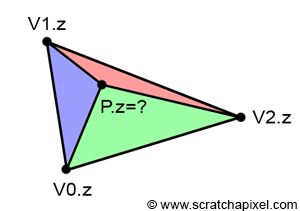
图 3:我们可以通过使用重心坐标对三角形顶点 z 坐标进行插值来找到 P 的深度吗?
希望深度缓冲区的原理简单易懂。 我们现在需要做的就是解释如何计算深度值。 首先,让我们再次重复一下深度值是什么。 当一个像素与一个三角形重叠时,它会与三角形表面上的一个小表面重叠,正如引言中提到的,我们将其简化为一个点(图1中的点P)。 我们在这里要找到的是该点的 z 坐标。 正如本章前面提到的,如果我们知道三角形顶点的 z 坐标(我们这样做,它们存储在投影点的 z 坐标中),我们需要做的就是使用 P 的重心坐标对这些坐标进行插值(图 4):
图 4:通过线性插值求出点的 y 坐标
计算公式如下:
从技术上讲,这听起来很合理,但不幸的是,它不起作用。 让我们看看为什么。 问题不在于公式本身,它完全没问题。 问题是,一旦三角形的顶点被投影到画布上(一旦我们执行了透视分割),那么 z(我们想要插值的值)就不再在 2D 三角形的表面上线性变化。 通过 2D 示例更容易演示这一点。
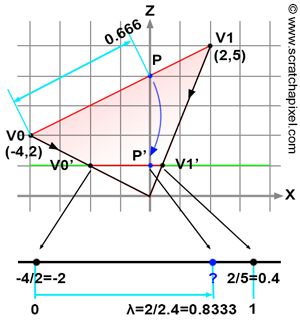
秘密就在图 4 中。想象一下,我们想要找到 2D 空间中由两个顶点 V0 和 V1 定义的一条线的“图像”。 画布由水平绿线表示。 这条线距坐标系原点 1 个单位(沿 z 轴)。 如果我们从 V0 和 V1 追踪直线到原点,那么我们就会在两个点处与绿线相交(在图中表示为 V0' 和 V1')。 该点的 z 坐标为 1,因为它们位于画布上,距原点 1 个单位。 使用透视投影可以轻松计算点的 x 坐标。 我们只需要将原始顶点的 x 坐标除以 z 坐标即可。 我们得到:
练习的目标是找到 P 的 z 坐标,P 是由 V0 和 V1 定义的直线上的一个点。 在这个例子中,我们对 P 的了解就是它在绿线上的投影 P' 的位置。 P'的坐标是{0,1}。 该问题类似于尝试查找像素重叠的三角形上的点的 z 坐标。 在我们的示例中,P' 是像素,P 是像素重叠的三角形上的点。 我们现在需要做的是计算 P' 相对于 V0' 和 V1' 的“重心坐标”。 我们将结果值称为 λ 。 与我们的三角形重心坐标一样,λ 也在 [0,1] 范围内。 要找到 λ ,我们只需获取 V0' 和 P' 之间的距离(沿 x 轴),然后将该数字除以 V0' 和 V1' 之间的距离。 如果使用 λ 对原始顶点 V0 和 V1 的 z 坐标进行线性插值来求出 P 的深度,那么我们应该得到数字 4(通过看图我们很容易看出 P 的坐标为 {0 ,4})。 我们首先计算 λ :
如果我们现在对 V0 和 V1 z 坐标进行线性插值来找到 P z 坐标,我们会得到:
这不是我们期望的值! 在本例中使用 P 的“重心坐标”或 λ 对原始顶点 z 坐标进行插值来查找 P z 坐标是行不通的。 为什么? 原因很简单。 透视投影保留线条但不保留距离。 从图 4 中很容易看出,V0 和 P 之间的距离与 V0 和 V1 之间的距离的比率 (0.666) 与 V0' 和 P' 之间的距离与 V0 之间的距离的比率不同。 ' 和 V1' (0.833)。 如果 λ 等于 0.666 就可以正常工作,但问题是,它等于 0.833! 那么,我们如何求出P的z坐标呢?
该问题的解决方案是通过使用 λ 对顶点 V0 和 V1 z 坐标的倒数进行插值来计算 P的z 坐标的倒数。 换句话说,解决方案是:
让我们检查一下它是否有效:
如果现在取这个结果的倒数,我们就得到 P的z 坐标的值 4。这是正确的结果! 如前所述,解决方案是使用重心坐标对顶点的 z 坐标进行线性插值,然后反转结果数以找到 P 的深度(其 z 坐标)。 对于我们的三角形,公式是:
图 5:透视投影保留线条,但不保留距离
现在让我们更正式地研究这个问题。 为什么我们需要对顶点的逆 z 坐标进行插值? 正式的解释有点复杂,如果你愿意的话可以跳过。
让我们考虑相机空间中由两个顶点定义的线,其坐标分别表示为 (X0,Z0) 和 (X1,Z1)。 这些顶点在屏幕上的投影分别表示为 S0 和 S1(在我们的示例中,我们假设相机原点和画布之间的距离为 1,如图 5 所示)。 我们将 S 称为 S0 和 S1 定义的直线上的点。 S 在 2D 线上有一个对应的点 P,其坐标为 (X,Z = 1)(在本例中我们假设投影点的屏幕或垂直线距坐标系原点 1 个单位)。 最后,参数 t 和 q 的定义如下:
我们也可以写成:
因此,可以通过插值计算点 P 的 (X,Z) 坐标(等式 1):
类似地(等式 2):
S 是一个一维点(它已投影在屏幕上),因此它没有 z 坐标。 S 也可以计算为:
因此:
如果我们将分子替换为方程 1,将分母替换为方程 2,则我们得到(方程 3):
我们也得到:
因此(等式 4):
如果现在将方程 3 中的 X0 和 X1 替换为方程 4,我们得到(等式5):
记住等式 1(等式 6):
如果结合方程 5 和 6,我们得到:
可以简化为:
我们现在可以用 q 来表达参数 t:
如果代入等式 6 中的 t,我们得到:
因此可以得到:
这就是我们最终想要得到的公式。
3、其他可见表面算法
正如简介中提到的,z 缓冲区算法属于隐藏表面去除或可见表面算法系列。 这些算法可以分为两类:对象空间算法和图像空间算法。 本课我们没有讨论的“painter”算法属于前者,而z-buffer算法则属于后者。 painter算法背后的概念大致是从后到前绘制或绘制对象。 该技术需要对对象进行深度排序。 正如本章前面所解释的,第一个对象以任意顺序传递到渲染器,然后当两个三角形彼此相交时,很难弄清楚哪个三角形在另一个前面(从而决定应该绘制哪个三角形) 第一的)。 该算法已不再使用,但 z 缓冲区非常常见(GPU 使用它)。
原文链接:可见性和深度缓冲区算法 - BimAnt