初级数据结构(二)——链表
| 文中代码源文件已上传:数据结构源码 <-上一篇 初级数据结构(一)——顺序表 | 初级数据结构(三)——栈 下一篇-> |
1、链表特征
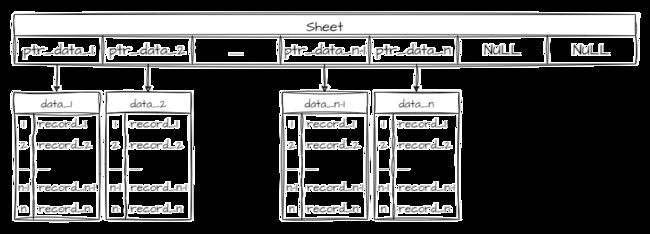
与顺序表数据连续存放不同,链表中每个数据是分开存放的,而且存放的位置尤其零散,毫无规则可言。对于零散的数据而言,我们当然可以通过某种方式统一存储每一个数据存放的地址,如下图:
但这个 sheet 无论怎么看都是一个数组,而 ptr_data 是个指针,也就是说,以上数据结构仍然是一种顺序表,只不过表中的数据从具体的值改为指针。它仍然没有脱离顺序表的范畴。自然顺序表的优势及劣势它也照单全收。
顺序表的劣势在于,开辟空间并非随需开辟,释放空间也显得不那么灵活。如果顺序表做到每次增加数据便拓展空间,删除数据便回收空间,基于 realloc 可能异地开辟的特点,搬运数据的时间复杂度为 O(N) 。如果顺序表的长度是几千万乃至几亿,每添加或者删除一个数据,其延迟是难以忽略的。因此上篇中的顺序表每次开辟空间均是成批开辟。但这种方式也必然造成空间的浪费。
如果有一种储存方式可以解决上述问题,做到每一个数据的空间都按需开辟,且按需释放,那么在最极端的情况下,它甚至可以节省近一半存储空间。在此思想上,数组的特性完全不符合该要求,首先需要抛弃的便是数组。但上图倘若没了数组,每一个数据节点的位置便无从知晓。于是有了链表的概念。
链表可以将下一个节点的位置储存在上一个节点中,此外还可以将上一个节点的位置储存在下一个节点中。
如上图。链表还需要一个头指针指向第一个节点。上述结构称为单链表。此外链表还有以下常见结构(环链、双向链)。
比如这篇文章最顶端“上一篇”、“下一篇”的导航链接就类似双向链。
2、链表创建
2.1、文件结构
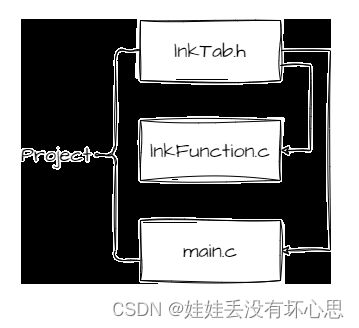
本文以最基本的单链为例,因为其他变形比单链的复杂程度高不了多少,有机会再作补充。仍是先从文件结构开始,分别建立以下三个文件,
lnkTab.h :用于创建结构体类型及声明函数;
lnkFunction.c :用于创建链表各种操作功能的函数;
main.c :仅创建 main 函数,用作测试。
2.2、前期工作
在 lnkTab.h 中先码入以下内容:
#include
#include
#include
//自定义数据类型和打印类型,方便后续更改储存数据的类型
#define PRINT_FORMAT "%d"
typedef int DATATYPE;
//创建链表节点的结构体类型
typedef struct LinkedListType
{
DATATYPE data;
struct LinkedListType* next;
}LinkedListType;
//---------------------函数声明---------------------
//打印链表
extern void DataPrint(LinkedListType*);
//创建节点
extern LinkedListType* NodeCreate(const DATATYPE, const LinkedListType*);
//销毁链表
extern void DataDestory(LinkedListType**); 在 lnkFunction.c 中包含 lnkTab.h 并分别创建一个打印链表和销毁链表的函数:
#include "lnkTab.h"
//打印链表
void DataPrint(LinkedListType* ptr_headNode)
{
//创建节点指针
LinkedListType* currentNode = ptr_headNode;
//循环打印
while (currentNode)
{
//打印
printf(PRINT_FORMAT" -> ", currentNode->data);
//移动节点指针
currentNode = currentNode->next;
}
printf("NULL\n");
}
//创建节点
LinkedListType* NodeCreate(const DATATYPE data, const LinkedListType* next)
{
LinkedListType* node = (LinkedListType*)malloc(sizeof(LinkedListType));
//加入判断防止空间开辟失败
if (node == NULL)
{
perror("Malloc Fail");
return NULL;
}
//节点赋值
node->data = data;
node->next = next;
return node;
}
//销毁链表
void DataDestory(LinkedListType** ptr2_headNode)
{
//空链表判断
if (!ptr2_headNode) return;
//创建节点指针
LinkedListType* currentNode = *ptr2_headNode;
//循环逐个销毁节点
while (currentNode)
{
LinkedListType* nextNode = currentNode->next;
free(currentNode);
currentNode = nextNode;
}
//头指针置空
*ptr2_headNode = NULL;
}最后在 main.c 中包含 lnkTab.h,并创建一个链表头指针:
#include "lnkTab.h"
int main()
{
LinkedListType* ptr_headNode = NULL;
return 0;
}至此,前期工作准备完毕。
3、链表操作
3.1、增
同顺序表一样,链表除了指定位置插入数据之外,最好也定义下头部插入数据及尾部插入数据的函数。因此先在 lnkTab.h 中加入以下函数声明:
//指定位置插入数据
extern void DataPush(LinkedListType**, const int, const DATATYPE);
//头部插入数据
extern void DataPushHead(LinkedListType**, const DATATYPE);
//尾部插入数据
extern void DataPushTail(LinkedListType**, const DATATYPE);之后先创建 DataPush 函数。在此之前把函数的流程图画出,以助于思考。画流程图的过程中能认识到空链表跟非空链表要分开处理,除了头插,其他位置插入的逻辑是相同的:
对照上图,照着在 lnkFunction.c 里写出如下代码:
void DataPush(LinkedListType** ptr2_headNode, const int pos, const DATATYPE data)
{
//有效性检查
if (!ptr2_headNode) return;
LinkedListType* currentNode = *ptr2_headNode;
//如果插入位置小于等于0或者没有节点
if (pos <= 0 || !currentNode)
{
//创建节点,将头指针的值赋予该节点的指向,并将头指针指向该节点
LinkedListType* node = NodeCreate(data, currentNode);
*ptr2_headNode = node;
return;
}
//遍历节点至插入位置前一节点
for (int i = 0; i < pos - 1; i++)
{
//若遇到最后一个节点则停止遍历,当前节点指针指向最后一个节点
if (currentNode->next)
currentNode = currentNode->next;
else
break;
}
//创建节点,将当前节点的指向值赋予创建的该节点的指向,并将当前节点指向创建的节点
LinkedListType* node = NodeCreate(data, currentNode->next);
currentNode->next = node;
}至于头插尾插数据,只不过是上述函数 pos 位置的区别。因此:
//pos = 0 便是头插
void DataPushHead(LinkedListType** ptr2_headNode, const DATATYPE data)
{
DataPush(ptr2_headNode, 0, data);
}
//由于 DataPush 函数在 pos 大于节点数时自动进行尾插
//因此 pos = INT_MAX 在任意情况下都是尾插
void DataPushTail(LinkedListType** ptr2_headNode, const DATATYPE data)
{
DataPush(ptr2_headNode, INT_MAX, data);
}验证环节。在 main 函数中加入如下代码试运行:
DataPush(&ptr_headNode, 10, 1234);
DataPrint(ptr_headNode); // 1234 NULL
DataPushTail(&ptr_headNode, 1);
DataPrint(ptr_headNode); // 1234 1 NULL
DataPushHead(&ptr_headNode, 2);
DataPrint(ptr_headNode); // 2 1234 1 NULL
DataPushTail(&ptr_headNode, 3);
DataPrint(ptr_headNode); // 2 1234 1 3 NULL
DataPush(&ptr_headNode, 1, 14542);
DataPrint(ptr_headNode); // 2 14542 1234 1 3 NULL
DataPushHead(&ptr_headNode, 4);
DataPrint(ptr_headNode); // 4 2 14542 1234 1 3 NULL
DataPushTail(&ptr_headNode, 114514);
DataPrint(ptr_headNode); // 4 2 14542 1234 1 3 114514 NULL
DataPush(&ptr_headNode, 10, 1442);
DataPrint(ptr_headNode); // 4 2 14542 1234 1 3 114514 1442 NULL结果与预期无误。至此插入功能便已完成。
3.2、删
第一步当然是在 lnkTab.h 中加入函数声明:
//指定位置删除数据
extern void DataPop(LinkedListType**, const int, const int);
//头部删除数据
extern void DataPopHead(LinkedListType**);
//尾部删除数据
extern void DataPopTail(LinkedListType**);完毕后,二话不说,先上流程图。这里同样要注意区分空链和其他位置删除。不过删除节点还得将头删及其他位置删除分开判定。
而且这里要注意的是,删除与插入不同,万一 pos 值传错导致小于 0 或者大于链表长度,便不能如上图简单粗暴地执行头删尾删。创建函数的时候多加一个参数来判断是否要在这种情况下头删或者尾删最好不过了。为了直观,还是在 lnkTab.h 头文件中加个枚举类型:
//定义删除节点的暴力模式和非暴力模式
enum Deletion { UNFORCED, FORCED };然后,在 lnkFunction.c 里码下这些:
void DataPop(LinkedListType** ptr2_headNode, const int pos, const int deletionMode)
{
//如果没有节点则直接退出
if (!ptr2_headNode || !*ptr2_headNode) return;
LinkedListType* currentNode = *ptr2_headNode;
//如果插入位置小于等于0则头删,前提是在非暴力模式下
if (pos == 0 || (pos < 0 && deletionMode))
{
*ptr2_headNode = (*ptr2_headNode)->next;
free(currentNode);
return;
}
//遍历节点至需要删除的节点前一节点
int i;
for (i = 1; i <= pos - 1; i++)
{
//若遇到倒数第二个节点则停止遍历,当前节点指针指向倒数第二个节点
if (currentNode->next->next)
currentNode = currentNode->next;
else
break;
}
//模式不暴力的话,pos超出表长度就直接退出了
if (i < pos - 1 && !deletionMode) return;
//删!
LinkedListType* freeNode = currentNode->next;
currentNode->next = currentNode->next->next;
free(freeNode);
}然后头删 pos 为 0 ,尾删 pos = INT_MAX 且删除模式为 FORCED 。就没必要再赘述了:
//删除头部节点
void DataPopHead(LinkedListType** ptr2_headNode)
{
DataPop(ptr2_headNode, 0, UNFORCED);
}
//删除尾部节点
void DataPopTail(LinkedListType** ptr2_headNode)
{
DataPop(ptr2_headNode, INT_MAX, FORCED);
}题外话,这里再提另一种更安全的方式, 指定位置删除的 pos 如果超出链表范围直接报错,然后头删尾删单独写:
//删除头部节点
void DataPopHead(LinkedListType** ptr2_headNode)
{
if (!ptr2_headNode) return;
LinkedListType* currentNode = *ptr2_headNode;
//如果没有节点则直接退出
if (currentNode == NULL) return;
//将头指针置为第一个节点的指向,并释放第一个节点
*ptr2_headNode = currentNode->next;
free(currentNode);
}
//删除尾部节点
void DataPopTail(LinkedListType** ptr2_headNode)
{
if (!ptr2_headNode) return;
LinkedListType* currentNode = *ptr2_headNode;
//如果没有节点则直接退出
if (currentNode == NULL) return;
//如果只有一个节点则采用头删
else if (currentNode->next == NULL)
{
DataPopHead(ptr2_headNode);
return;
}
//遍历至倒数第二个节点,释放最后一个节点,并将倒数第二个节点指向置空
else
{
while (currentNode->next->next)
{
currentNode = currentNode->next;
}
free(currentNode->next);
currentNode->next = NULL;
}
}回归正题,之后是熟悉的测试阶段。 main 函数中添加:
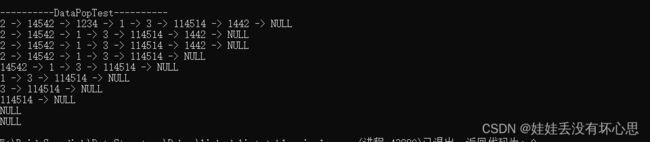
printf("\n----------DataPopTest----------\n");
DataPop(&ptr_headNode, 0, UNFORCED);
DataPrint(ptr_headNode); // 2 14542 1234 1 3 114514 1442 NULL
DataPop(&ptr_headNode, 2, UNFORCED);
DataPrint(ptr_headNode); // 2 14542 1 3 114514 1442 NULL
DataPop(&ptr_headNode, 1000, UNFORCED);
DataPrint(ptr_headNode); // 2 14542 1 3 114514 1442 NULL
DataPop(&ptr_headNode, 1000, FORCED);
DataPrint(ptr_headNode); // 2 14542 1 3 114514 NULL
DataPop(&ptr_headNode, 0, UNFORCED);
DataPrint(ptr_headNode); // 14542 1 3 114514 NULL
DataPop(&ptr_headNode, 0, UNFORCED);
DataPrint(ptr_headNode); // 1 3 114514 NULL
DataPop(&ptr_headNode, 0, UNFORCED);
DataPrint(ptr_headNode); // 3 114514 NULL
DataPop(&ptr_headNode, 0, UNFORCED);
DataPrint(ptr_headNode); // 114514 NULL
DataPop(&ptr_headNode, 0, UNFORCED);
DataPrint(ptr_headNode); // NULL
DataPop(&ptr_headNode, 0, UNFORCED);
DataPrint(ptr_headNode); // NULL 完事!
3.3、改和查
这两个功能简直不要太简单。查的逻辑跟打印逻辑一致,至于改,用查的功能返回节点地址,直接改 data 完事。
lnkTab.h :
//查找节点
extern LinkedListType* DataSearch(const LinkedListType*, const DATATYPE);
//修改节点
extern void DataModify(const LinkedListType*, DATATYPE, DATATYPE);lnkFunction.c:
//查找节点
LinkedListType* DataSearch(const LinkedListType* ptr_headNode, const DATATYPE data)
{
LinkedListType* currentNode = ptr_headNode;
while (currentNode)
{
if (currentNode->data == data) break;
currentNode = currentNode->next;
}
return currentNode;
}
//修改节点
void DataModify(const LinkedListType* ptr_headNode, DATATYPE target, DATATYPE replace)
{
LinkedListType* node = DataSearch(ptr_headNode, target);
if (!node) return;
node->data = replace;
}main.c 测试:
printf("\n----------DataSearchModifyTest----------\n");
for (int i = 20; i >= 10; i--)
{
DataPushHead(&ptr_headNode, i);
}
DataPrint(ptr_headNode); // 10 12 13 14 15 16 17 18 19 20 NULL
DataModify(ptr_headNode, 3, 23457);
DataPrint(ptr_headNode); // 10 12 13 14 15 16 17 18 19 20 NULL
DataModify(ptr_headNode, 13, 23457);
DataPrint(ptr_headNode); // 10 12 23457 14 15 16 17 18 19 20 NULL搞定!准备下一篇。撒花!
4、作点补充
一开始就提到双向链表和环链。虽然结构复杂了,但是这两种结构比单链简单太多了。可以说学懂了单链,那么其他结构的链表跟玩似的。
以另一个常规的极端(不考虑中途环状),环状双向链举例。在数据操作的代码上,这个结构可比单链节省了寻找尾节点以及记录上一个节点指针的麻烦。
双向链如果一直找上一个( prev )节点,它也只不过是另一种单链,视作 next 结构的倒序。最直观的在于链表倒置:
while(currentNode)
{
DATATYPE* nextNode = currentNode->next;
currentNode->next = currentNode->prev;
currentNode->prev = temp;
currentNode = nextNode;
}一个循环搞定整个链表导致,而如果是单链,需要考虑遍历分别头插之类的,代码量直线上升。至于环链,尾节点的 next 指向头节点。事实上这种结构提供了寻找尾节点的便利( currentNode->prev )。那是更便利了,只不过不支持迭代,总有牺牲嘛。
构建节点的结构体特别自由,链表也就那么几种大体结构,细节没有规定。总之,只要实现节点内记录其他节点的信息便属于链表。奥力给!