【数据结构和算法】--- 栈

栈的概念及结构

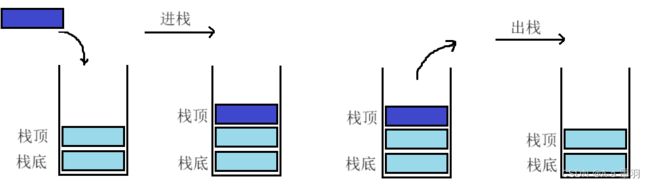
栈是一种特殊的线性表。相比于链表和顺序表，栈只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

• 压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
• 出栈：栈的删除操作叫做出栈。出数据也在栈顶。

联想一下，其实栈就相当于手枪的弹夹，将子弹压入弹夹的操作就相当于压栈，打出子弹的操作就相当于出栈，每次先打出的子弹都是我们最后压入弹夹的子弹，最后一颗子弹就是我们最先压入的那一颗了，这就是后进先出。栈也如此，结构大致如下：

基于这样的结构，那么如果我们想要拿到栈的某个元素，就必须要先把此元素以上的元素依次出栈，然后才能取出。

栈的实现

有两种方式可以实现栈结构-数组栈，链式栈：

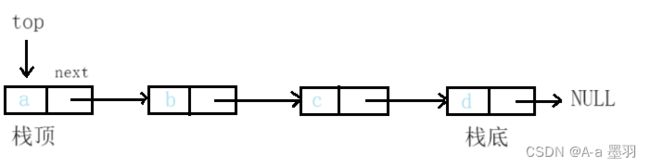
1. 链式栈
   如果用单链表实现：若栈底就指向头节点，栈顶就指向尾节点。这样设计入栈很方便，相当于头插，时间复杂度为O(1)；但出栈操作就必须要先遍历链表找到栈顶的前一个，然后再出栈，并修改栈顶，相当于尾删，时间复杂度达到O(N)。于是乎我们一般将栈顶指向头节点，栈底指向尾节点，这样入栈出栈就都是O(1)了，即头插/头删。

如果用双向链表实现：栈顶为链表的头和尾都可以，入栈和出栈时间复杂度都为O(1)，但双向链表结构较为复杂，一般不选用此结构

2. 数组栈
   数组栈的入栈和出栈的实现较为简单，且时间复杂度为O(1)

相较于链式栈，数组栈访问数据时cpu缓存命中率比较高，但链式栈相较于数组栈也会节省一定的空间。下面栈的实现主要用的是数组栈。
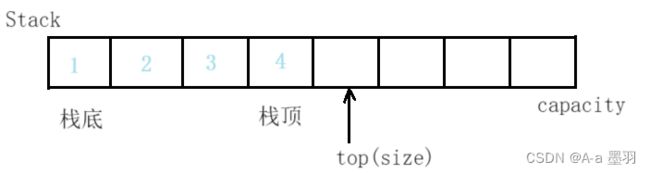
通常我们标识栈顶位置的下一个位置为top(即下标为size的位置)。与标识栈顶位置为top相比较，这样可以减少栈为空，栈容量判断等函数的难度，且若标识栈顶位置为top，当栈里面没有元素时top的指向也较为尴尬。
我们可以如下定义栈结构：

typedef int STDataType;
//数组栈
typedef struct stack
{
	STDataType* a;
	int top;//标识栈顶下一个元素下标（同为栈元素个数）
	int capacity;
}ST;

初始化栈

通过上面对栈的介绍进行初始化。

//初始化
void StackInit(ST* pst)
{
	assert(pst);
	pst->top = 0;
	pst->capacity = 0;
	pst->a = NULL;
}

入栈

入栈操作就是向数组内增加一个数，首先要判断栈（数组）容量pst->capacity是否需要增容，然后向top位置（即pst->a[top]）增加一个数，最后重新变换top指向（即pst->top++），具体如下：

//入栈
void StackPush(ST* pst, STDataType x)
{
	assert(pst);
	//判断增容
	if (pst->top == pst->capacity)
	{
		int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
		STDataType* newnode = (STDataType*)realloc(pst->a, sizeof(ST) * newcapacity);
		if (newnode == NULL)
		{
			perror("check_ST_capacity()::malloc");
			return;
		}
		pst->a = newnode;
		pst->capacity = newcapacity;
	}
	//目标数x入栈
	pst->a[pst->top] = x;
	//变换top指向
	pst->top++;
}

出栈

出栈操作就相对简单了，直接改变top指向就可以了（即pst->top--）。如果栈里面已经没有元素了，那执行此操作top指向就会错误，于是乎我们需要断言一下来确保栈里面有元素可以删除（即assert(ps->top != 0);）。

//出栈
void StackPop(ST* pst)
{
	assert(pst);
	assert(pst->top != 0);
	pst->top--;
}

其他一些栈函数

1. 获得栈顶元素：
   pst->top指向的是栈顶的下一个元素的下标，那么只需要让他--即可（即pst->a[pst->top-1]），在使用前确保栈中有元素，不然程序会崩溃（越界访问）。

// 获取栈顶元素 
STDataType StackTop(ST* pst)
{
	assert(pst);
	assert(pst->top != 0);
	return pst->a[pst->top - 1];
}

2. 获得栈有效元素个数：
   pst->top指向的既是指向栈顶下一个元素的下标也是整个栈里面有效数据的个数，所以此函数返回pet->top即可。

// 获取栈中有效元素个数
int StackSize(ST* pst)
{
	assert(pst);
	return pst->top;
}

3. 检查栈是否为空：
   同理只要栈里面有效元素个数为0，那么栈就是空栈，如下：

// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
bool StackEmpty(ST* pst)
{
	assert(pst);
	return pst->top == 0;
}

4. 栈的销毁：
   栈的销毁本质上是释放先前realloc()开辟的数组，再将容量和栈顶置0即可。

// 销毁栈 
void StackDestroy(ST* pst)
{
	assert(pst);
	assert(pst->capacity != 0);
	free(pst->a);
	pst->a = NULL;
	pst->top = pst->capacity = 0;
}

---

小结

• 栈是一种后进先出的结构，这一点恰与我们后面要讲的队列相反；

• 顺序表和链表都可以用来实现栈，不过一般都使用顺序表，因为栈想当于是阉割版的顺序表，只用到了顺序表的尾插和尾删操作，顺序表的尾插和尾删不需要搬移元素,因此效率非常高O(1)，故一般都是使用顺序表实现；

• 栈结构中的top一般为要插入位置的下标（即栈顶元素下一个位置），这是为了方便区分栈为空栈的情况，且后续函数更好实现；

• 栈只能在栈顶进行输入的插入和删除操作，不支持随机访问；

---

栈相关的题目

1. 关于入栈和出栈顺序，如下：

若进栈序列为 1,2,3,4 ，进栈过程中可以出栈，则下列不可能的一个出栈序列是（）
A 1,4,3,2
B 2,3,4,1
C 3,1,4,2
D 3,4,2,1

不难看出是c选项错了，因为如果第一个出栈的是3，那么在3之前压栈的1和2就都还没有出栈，所以接下来出栈的只能有两种情况：

• 1.4接着入栈然后出栈，即为D选项；
• 2.直接出先前压栈的2。

对于C选项，此时的1还在栈底，在它上面还有2，所以不能直接出1。

2. LeetCode OJ题： 有效的括号

题目描述：给定一个只包括 '('，')'，'{'，'}'，'['，']'的字符串s ，判断字符串是否有效。
有效字符串需满足：

• 左括号必须用相同类型的右括号闭合。
• 左括号必须以正确的顺序闭合。
• 每个右括号都有一个对应的相同类型的左括号。

这题主要考察我们对栈特性的应用，即后进先出，那么我们便可这样设计：循环遍历字符串s中的每个字符，满足以下条件的对栈进行入/出栈操作：

1. 遇到左括号，直接入栈；
2. 遇到右括号，取栈顶元素进行匹配，若不匹配直接返回false，若匹配就将此括号出栈，并继续循环。

另外我们还要对如下两种情况做出判断：

1. 当遍历到右括号时，此时栈中是否还有元素？（QueueEmpty()?）为空直接返回false；
2. 当字符串s遍历结束时，栈中是否还有剩余元素？（QueueEmpty()?）不为空直接返回false，为空返回true。

其中一些栈的接口函数就不展示了，上面内容都有，代码实现如下：

bool isValid(char* s)
{
    ST st;//创建栈
    StackInit(&st);//初始化栈
    //遍历字符串s
    while(*s)
    {
        if(*s == '(' || *s == '[' || *s == '{')
        {
            StackPush(&st,*s);
        }
        else
        {
            //栈为空判断，为空返回false，如上讲解1处
            if(StackEmpty(&st))
            {
                StackDestroy(&st);
                return false;
            }
            char ch = StackTop(&st);
            //左右括号匹配判断，匹配错误返回false
            if((*s == ')' && ch != '(') || 
               (*s == ']' && ch != '[') ||
               (*s == '}' && ch != '{'))
                {
                    StackDestroy(&st);
                    return false;
                }
            StackPop(&st);
        }
        s++;
    }
    //栈为空判断，不为空返回false,与上面判断处区分，如上讲解2处
    if(!StackEmpty(&st))
    {
        StackDestroy(&st);
        return false;
    }
    return true;
}