5.基本统计方法-连续性变量的组间比较

目录

1.两样本的定量变量的假设检验

1.1 单样本t检验

1.2 两独立样本t检验

1.3 配对样本t检验

1.4 正态性检验和方差齐性检验

2.多样本定量变量的假设检验

2.1 基本知识

2.2 单因素方差分析

2.3 单因素的协方差分析：

2.4 两因素方差分析

重复测量的方差分析

随机区组设计方差分析

交叉设计方差分析

析因设计变量的方差分析

2.5 多元方差分析

2.6 非参数检验

---

1.两样本的定量变量的假设检验

进行t检验的两个前提：（1）随机样本；（2）样本来自的总体服从正态分布；（2）两独立样本比较时要求组间总体方差齐

1.1 单样本t检验

#单样本t检验，也即是样本均数与总体均数比较

daily.intake <- c(5260,5470,5640,6180,6390,6515,
                  6805,7515,7515,8230,8770)
mean(daily.intake)
sd(daily.intake)
quantile(daily.intake)#向量的统计描述直接用计算函数进行计算

t.test(daily.intake,mu=7725)#总体均数为7725

One Sample t-test

data:  daily.intake
t = -2.8208, df = 10, p-value = 0.01814
alternative hypothesis: true mean is not equal to 7725
95 percent confidence interval:
 5986.348 7520.925
sample estimates:
mean of x
 6753.636

    输出的结果会自动给出t统计量，自由度，p值，以及备择假设内容，样本的95%置信区间，样本均数。如果需要将置信区间改为99%，需要使用参数conf.level=0.99，单侧或双侧检验可以使用参数alt="two.sided", "less", "greater"。

当样本不满足正态分布时，只能使用秩和检验：

wilcox.test(daily.intake, mu=7725)

1.2 两独立样本t检验

胖子和瘦子的能量消耗是否存在差异？

library(ISwR)
attach(energy)
energy
t.test(expend~stature, var.equal=T)

 #参数var.equal用于设置方差是否具有齐性，默认为F
#系统默认为95%置信区间，可以通过conf.level设置为99%，

#参数alt进行单侧检验,取值包括c("two.sided", "less", "greater")

当两样本所属的总体均为正态，但是方差不齐，需要采用t‘检验，也即是校正t检验，对自由度进行校正。下列结果可以看到自由度是经过校正。

t.test(expend~stature, var.equal=F)

Welch Two Sample t-test

data:  expend by stature
t = -3.8555, df = 15.919, p-value = 0.001411
alternative hypothesis: true difference in means between group lean and group obese is not equal to 0
95 percent confidence interval:
 -3.459167 -1.004081
sample estimates:
 mean in group lean mean in group obese
           8.066154           10.297778

比如现在比较一下胖子的消耗是不是比瘦子多，这就为单侧检验。

t.test(expend~stature,alt="less",var.equal=T,conf.level=0.99)

！！！在实际工作中，有时总体的分布不易确定，或不符合参数检验的条件，则需要应用不依赖于总体分布类型的统计推断方法，非参数检验：

wilcox秩和检验基于秩次的非参数检验，用于两组独立样本定量资料或等级资料的比较

wilcox.test(expend~stature,data=energy)
wilcox.test(x,y)

x,y为两独立样本结果，expend~stature，第一个参数为结果值，第二个参数为分组变量。

1.3 配对样本t检验

配对设计包括有同体配对；异体配对。

比较个体绝经前和绝经后摄入量是否存在差异，此研究为样本配对。在t检验的基础上，使用参数paired=T

attach(intake)
intake
t.test(pre, post, paired=T)

#10份乳酸饮料使用脂肪酸水解法和骡子哥特立法测定结果，，比较两种方法是否有存在差异。

x <- c(0.84,0.59,0.67,0.63,0.69,0.98,0.75,0.73,1.20,0.87)
y <- c(0.58,0.51,0.50,0.32,0.34,0.52,0.45,0.51,1.00,0.51)
t.test(x,y,paired=T)

当配对样本总体不满足正态分布时，只能使用wilcox符号秩和非参数检验：

wilcox.test(x,y,paired = T)
wilcox.test(pre,post,paired = T)

1.4 正态性检验和方差齐性检验

1.4.1 方差齐性检验：

通过函数var.test()可以判断两个样本的方差齐性，p>0.1说明方差齐，为了提高检验敏感性α往往取0.1。

var.test(expend~stature)
var.test(x,y)

bartlett.test(energy$expend,
              energy$stature)
bartlett.test(expend~stature,data=energy)

library(car)
leveneTest(expend~stature,data=energy)

#bartlett检验对数据的正态性非常敏感，而levene检验是一种非参数方法，不依赖于数据分布类型，其适用范围更广。数据为两样本结果x，y时，使用var.test检验，使用baetlett.test会报错。

1.4.2 正态性检验：

中心极限定理：当每组样本量>=50时，可以认为样本的均数近似服从正态分布。当样本数n<50时，需要对每组资料进行正态性检验。

正态性检验常用的方法：矩法检验，W检验（shapiro-wilk W test），K-S检验（Kolmogorov-Smirnov test）和D检验。矩法检验比较保守，w检验比较灵敏。

函数shapiro.test（）

1.单样本可以直接用正态性函数进行检验，按α=0.1的水准，所以认为满足正态性检验

shapiro.test(daily.intake)

2.两样本的正态检验方法，使用tapply函数，按照stature分组进行shapiro检验

energy$stature <- factor(energy$stature,levels = c("lean","obese"))
str(energy)
tapply(expend,stature,shapiro.test)

3.利用QQ图判断

library(car)
qqPlot(lm(energy$expend~energy$stature),simulate=T,main="Q-Q Plot",labels=F)

点都基本落在95%的置信区间内，说明满足正态性假设。样本个数较少时，不太准确。

总结：在进行两独立样本均数比较时，应根据模型假设的要求选择合适的统计学方法。如果两样本均满足正态性和方差齐性，采用t检验；如果满足正态性，但方差不齐，采用校正t检验；如果任何一组数据不服从正态分布，则采用秩和检验。对于配对设计的定量资料，关键看差值是否符合正态分布，如果差值满足正态分布，可以采用配对t检验，否则，采用配对资料的符号秩和检验。

2.多样本定量变量的假设检验

t检验能否用于多组间均数比较？

t检验在多组之间进行两两比较，每次控制一类错误的概率为α=0.05，那么不犯一类错误概率为1-0.05=0.95，如果四个组进行比较，一共有6种两两比较的方式。不犯一类错误的概率为0.95^6=0.7351。所以随着比较次数的增多，犯一类错误的总概率将不断增大，并趋近于1。

第一类错误：如果假设H0实际是正确的，由于样本数据计算获得的检验统计量得出拒绝H0的结论，就犯了一类错误。（弃真，假阳性，用α来限制犯一类错误的概率）

第二类错误：原来H0不正确，但由于计算的检验统计量不能拒绝H0，此时犯了二类错误。（纳伪，假阴性，用β来限制二类错误的概率）

2.1 基本知识

实验设计：

1. 完全随机设计

        在实验研究中所考察的实验因素只有一个水平，其水平数视具体情况而定，且各组之间相互独立。

2.匹配设计：

（1）配对设计：将受试对象按某些特征或条件配成对子，然后把每队中的两个受试对象分到不同的处理组中，称为异体配对。自身配对处理前后从每个受试者身上观测到同一个变量的两个数值，将每个个体的这两个数值形成一个配对。

（2）随机区组设计：将全部的受试对象按某个或某些重要的属性（即区组因素，如窝别、体重或年龄）分组，把条件最接近的k个受试对象（k为实验因素的水平）视为同一个区组的个体，然后同完全随机的方法将每个区组中的全部受试对象分配到k个组中。

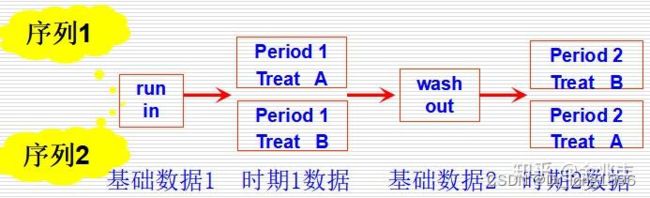
 （3）交叉设计：

        当研究者关心的实验因素有两个水平（A和B），而且希望这两个水平要先后作用于每一个受试者，一部分对象先接受A，后接受B，另一部分顺序相反。根据分组的特点，可以将交叉设计分为成组交叉设计和配对交叉设计。

 （4）析因设计

        当实验中涉及k(K>=2）个实验因素时，若将这k个因素的水平全面组合，设组合数为m，便有m个不同的实验条件，若m个实验条件同时实施，不分顺序，且各个因素对观测指标的影响地位相同，用以分析各个实验因素即它们互相配合的效应。

单独效应：是指其他因素的水平一定时，同一因素不同水平的差异。

主效应：某一因素在实验条件下效应的平均值

交互效应：若一个因素单独效应随另一个因素水平的变化而变化，且变化的幅度超过随机误差波动的范围。

（5）重复测量设计

        按实验分组因素将受试对象分成若干个组，每一个组受试对象接受一种特定的处理，在几个不同的时间点上从同一个受试对象身上重复获得变量的观测值，这种安排实验的方法叫做重复测量设计。

在R语言中方差分析可以使用aov()函数进行分析，此函数的使用方法如下所示：

aov(formula, data=data.frame)

表9-4中的y是因变量，字母A、 B、 C代表因子，函数中表达式（formula）符号及书写方法如下所示：

 常用一些表达式，小写字母x为定量变量：

 自变量位置顺序，顺序很重要很重要：

 1.表达式中效应的顺序在两种情况下会造成影响： (a)因子不止一个，并且是非平衡设计； (b)存在协变量。出现任意一种情况时，等式右边的变量都与其他每个变量相关。此时，我们无法清晰地划分它们对因变量的影响。例如，对于双因素方差分析，若不同处理方式中的观测数不同，那么模型y ~ A*B与模型y ~ B*A的结果不同。

2.样本大小越不平衡，效应项的顺序对结果的影响越大。一般来说，越基础性的效应越需要放在表达式前面。具体来讲，首先是协变量，然后是主效应，接着是双因素的交互项，再接着是三因素的交互项，以此类推。对于主效应，越基础性的变量越应放在表达式前面，因此性别要放在处理方式之前。有一个基本的准则：若研究设计不是正交的（也就是说，因子和/或协变量相关），一定要谨慎设置效应的顺序。

例如：含因子A、 B和因变量y的双因素不平衡因子设计，有三种效应： A和B的主效应， A和B的交互效应。假设你正使用如下表达式对数据进行建模： Y ~ A + B + A:B 有三种类型的方法可以分解等式右边各效应对y所解释的方差。

➢ 类型Ⅰ （序贯型）效应根据表达式中先出现的效应做调整。 A不做调整， B根据A调整， A:B交互项根据A和B调整。

➢ 类型Ⅱ（分层型）效应根据同水平或低水平的效应做调整。 A根据B调整， B依据A调整， A:B交互项同时根据A和B调整。

➢ 类型Ⅲ（边界型）每个效应根据模型其他各效应做相应调整。 A根据B和A:B做调整， A:B交互项根据A和B调整。

R默认调用类型I方法，其他软件（比如SAS和SPSS）默认调用类型Ⅲ方法。

此外，car包中的Anova()函数也可以进行方差分析。car包中的Anova()函数（不要与标准anova()函数混淆）提供了使用类型Ⅱ或类型Ⅲ方法的选项，而aov()函数使用的是类型I方法。

2.2 单因素方差分析

方差分析的基本思想：

方差分析的基本思想：前提是正态性、方差齐性、个体间独立随机

①首先将总变异分解为组间变异和组内变异。

②然后比较组间平均变异（组间均方）和组内平均变异（组内均方）。比较时采用两者的比值F值。

③若F值大于某个临界值，则可认为处理组间的效应不同；若F值小于某个临界值，可认为处理组间效应相同。

 在无处理因素作用，则组内变异和组间变异一样，只反映随机误差作用的大小，MS组间与MS组内比较接近，故在大多数情况下F在1附近随机波动，

R语言中使用函数aov()函数，来计算方差分析：

案例：multcomp 包中的 cholesterol 数据集， 50个患者均接受降低胆固醇药物治疗（trt）五种疗法中的一种疗法。哪种药物疗法降低胆固醇最多呢？

install.packages("multcomp")
library(multcomp)
data(cholesterol)
str(cholesterol)
leveneTest(response~trt,data=cholesterol)#方差齐性检验
tapply(cholesterol$response,cholesterol$trt,shapiro.test) #正态性检验
cholesterol.aov <- aov(response~trt,data=cholesterol)
summary(cholesterol.aov)

绘制各组的均数和置信区间：

library(gplots)
plotmeans(response ~ trt, xlab="Treatment", ylab="Response", 
          main="Mean Plot\nwith 95% CI")

多样本均数的两两比较（多重比较）：

#进一步找到哪两组之间的差异TukeyHSD()
TukeyHSD(cholesterol.aov)
plot(TukeyHSD(cholesterol.aov),las=1)#las表示横坐标文字的方向，有1，2两个选项。
#其他组间两两比较方法
pairwise.t.test(cholesterol$response,cholesterol$trt,p.adjust.method = "bonferroni")
#p.adjust.methods=c("holm", "hochberg", "hommel", "bonferroni", "BH", "BY",
#   "fdr", "none")

当比较次数过多>10次，bonferroni校正的检验方法效能过低，结论过于保守。

注意：因为方差分析本质也是一种特殊的线性拟合分析，所以可以采用线性模型进行多重比较。使用glht（model, linfct=mcp()）函数，这是R语言中较常用的多重比较的检验方法，可对多种统计模型进行检验，包括线性回归，广义线性模型。model是一个待检验的模型，这里为方差分析的结果，第二个参数linfct需要进行多重比较的假设，alt设置假设类型单侧，双侧，p_adjust.method校正P值得方法。

library(multcomp)
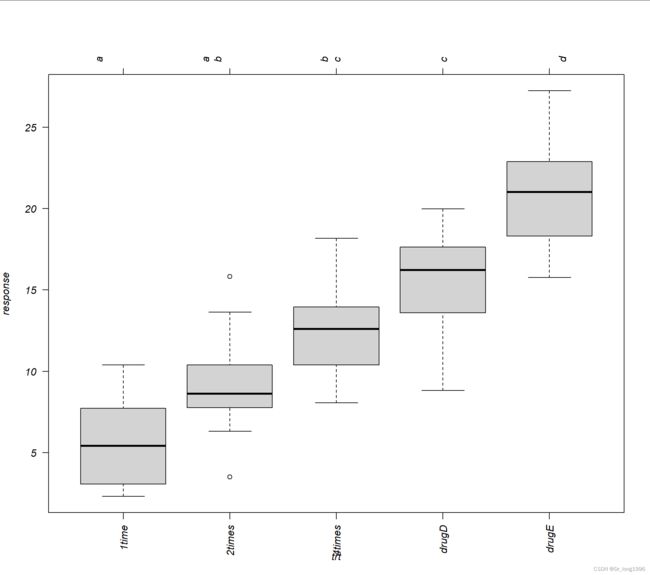
cholesterol.glht <-glht(cholesterol.aov,linfct = mcp(trt="Tukey"))
summary(cholesterol.glht)
plot(cld(cholesterol.glht,level=0.05),col="lightgrey")

 上图中有相同字母的组（用箱线图表示）说明均值差异不显著，如1time和2times差异不显著（有相同的字母a），而1time和4times差异显著（它们没有共同的字母）。从结果来看，使用降低胆固醇的药物时，一天四次5 mg剂量比一天一次20 mg剂量效果更佳，也优于候选药物drugD，但药drugE比其他所有药物和疗法都更优。

多重比较：TukeyHSD(模型)  glht(模型,linfct=mcp(B="Tukey"))，其中Tukey为不同类型之间两两比较，B为分组变量名称。

2.3 单因素的协方差分析：

单因素协方差分析（ANCOVA）扩展了单因素方差分析（ANOVA），包含一个或多个定量协变量。

案例：怀孕小鼠分成四组，每组接受不同剂量的药物处理，结局变量为产下的幼崽体重，协变量为怀孕时间。multcomp包中的litter数据集

data(litter)
str(litter)
aggregate(litter$weight,by=list(litter$dose),mean)#计算各组均值
plotmeans(litter$weight ~ litter$dose, xlab="Dose", ylab="weight", 
          main="Mean Plot\nwith 95% CI")
litter.aov <- aov(weight~gesttime+dose,data=litter)
summary(litter.aov)

协变量校正后的各组均值：由于使用了协变量，你可能想要获取调整的组均值，即去除协变量效应后的组均值。可使用effects包中的effects()函数来计算调整的。

library(effects)
effect("dose", litter.aov)

多重比较：

直接使用Tukey不能实现，使用glht函数来进行检测

library(multcomp)
summary(glht(litter.aov,linfct = mcp(dose="Tukey")))

可以看到只有一组是显著的，这时候退一步，我们只关心用药与否的差异比较，使用rbind和glht自定义比较的对象，如下所示：

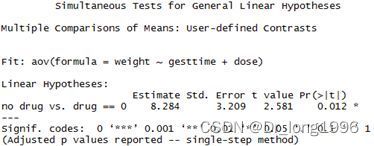
drug=rbind("no drug vs. drug"=c(3, -1, -1, -1))
summary(glht(litter.aov, linfct=mcp(dose=drug)))

函数glht允许通过向量乃至矩阵来设置比较的方法，c(3,-1, -1, -1)表示第一组与后面三组进行比较，也可以写成c(-3,1, 1, 1)，若是第一组与第三组比较则为c(1, 0, 1, 0)，这时只能为t检验。可以看出，药物施加对幼崽体重的影响是显著的。这个数字的设置没有明显影响，需要合并的组可以列为同一个数字1，不需要比较的组设置为0。

回归斜率同质性检验*****：

ANCOVA还假定回归斜率相同。本例中，假定四个处理组通过怀孕时间来预测出生体重的回归斜率都相同。 ANCOVA模型包含怀孕时间×剂量的交互项时，可对回归斜率的同质性进行检验。交互效应若显著，则意味着怀孕时间和幼崽出生体重间的关系依赖于药物剂量的水平。

litter.aov2 <- aov(weight~gesttime*dose,data=litter)
summary(litter.aov2)

交互项（gesttime:dose）的影响不显著，说明怀孕时间和药物剂量是独立的。如果影响显著，需要重新选择协变量。接下来我们可以将因变量、自变量、协变量关系进行可视化：

library(HH)
ancova(weight~gesttime+dose, data=litter)

 可以看到，不同分组回归线是平行的，进一步验证了等斜率性。施加药物后，幼崽体重降低。

2.4 两因素方差分析

案例：随机分配60只豚鼠，分别采用两种喂食方法（橙汁或维生素C），各喂食方法中抗坏血酸含量有三种水平（0.5mg、 1mg或2mg），每种处理方式组合都被分配10只豚鼠。牙齿长度为因变量。两个变量：喂食方法，剂量

data(ToothGrowth)
attach(ToothGrowth)
str(ToothGrowth)
table(ToothGrowth$supp,ToothGrowth$dose)
aggregate(len, by=list(supp,dose), FUN=mean)
aggregate(len, by=list(supp,dose), FUN=sd)
dose <- factor(dose)
ToothGrowth.aov <- aov(len ~ supp*dose,data = ToothGrowth)
summary(ToothGrowth.aov)

因为该案例中样本数是均衡的，所以supp和dose前后没有差别。supp*dose等价于supp+dose+supp：dose

interaction.plot(dose,supp,len,type="b",
                 las="1",
                 col=c("red","blue"),
                 pch=c(16,18),
                 main="Interaction between Dose and Supplement Type")
#type的含义是画的类型，p是点，l是线，b是点和线等
library(HH)
interaction2wt(len~supp*dose)

重复测量的方差分析

基本思想：

变异的分解：研究对象内的变异（重复测量因子的效应、处理因素与重复测量因素的交互效应）、研究对象间的变异（处理因素的效应），上述两者的交互作用，随机误差变异。

当处理因素与重复测量因素不存在交互效应时，要关注1.各处理组总体均数是否相等（处理因素的主效应是否为0）；2.各时间点的总体均数是否相等（时间因素的主效应是否为0）。当处理因素与重复测量因素存在交互效应，不在关注处理因素和时间因素的主效应检验结果，而是需要分别检验每个时点两种处理的总体均数是否相等，以及每个处理组各个时间点的总体均数是否全相等，称为简单效应检验。

因素：

受试者内因素：用于区分重复测量次数的变量，

受试者间因素：在重复测量时保持恒定的因素。

研究目的：

• 关注反应变量是否会随着时间发生改变，比较不同时间点的总体水平是否相同；
• 关注各处理组均数随时间变化趋势是否相同；
• 关注各处理组所有时间点的总体均数是否相同。

应用条件：

1.反应变量之间存在相关关系，比如细胞增殖，第二天数目是第一天数目影响的，第三天受第二天影响。

2.反应变量的均数向量服从多元正态分布

3.对于自变量各取值水平组合而言，反应变量的方差、协方差矩阵相等。

案例一：某一项营养学的实验中，将同种属、同月龄的16只大鼠随机分成两组，在同样的环境中，分别给予甲乙两种饲料，定期测量体重，计算每段时间的增重（g），试比较两种饲料的增重效果。

mice <- data.frame(group=c(rep(1,8),rep(2,8),rep(2,8),rep(2,8),rep(2,8),rep(2,8),rep(2,8),rep(2,8)),
                   food=c(rep("甲",8),rep("乙",8),rep("甲",8),rep("乙",8),rep("甲",8),rep("乙",8),rep("甲",8),rep("乙",8)),
                   number=c(1:16,1:16,1:16,1:16),
                   time=c(rep(2,16),rep(4,16),rep(6,16),rep(8,16)),
                   weight=c(33,25,38,25,24,32,28,16,17,19,16,17,21,18,23,30,40,34,33,36,32,33,35,20,22,23,24,25,24,25,26,37,31,33,29,
                            27,29,36,28,35,30,23,32,33,29,25,33,32,25,31,35,30,32,31,24,32,38,33,39,34,28,36,37,26))


mice2 <- data.frame(group=c(rep(1,8),rep(2,8)),
                   food=c(rep("甲",8),rep("乙",8)),
                   number=c(1:16),
                   time2=c(33,25,38,25,24,32,28,16,17,19,16,17,21,18,23,30),
                   time4=c(40,34,33,36,32,33,35,20,22,23,24,25,24,25,26,37),
                   time6=c(31,33,29,27,29,36,28,35,30,23,32,33,29,25,33,32),
                   time8=c(25,31,35,30,32,31,24,32,38,33,39,34,28,36,37,26))

mice2$group <- factor(mice2$group)#因子化分类变量
mice2$food<- factor(mice2$food)
mice2$number <- factor(mice2$number)

两种数据格式：往往在excel中收录的数据为第二种格式。

处理因素：饲料2个水平，重复测量因素时间4个水平，2周，4周，6周和8周。

分析目的：一是检验两组4个时间段的增重趋势是否一致（交互效应）；二是每组各时间段的平均增重是否相同（处理效应）；三是每个时间段两组的平均增重是否相同（重复测量效应）

应用条件检验：

判断异常值：

统计描述：

library(psych)  #调用包“psych”
describeBy(mice2$time2, group = mice2$group) #time2基本信息分组描述
describeBy(mice2$time4, group = mice2$group) #time4基本信息分组描述
describeBy(mice2$time6, group = mice2$group) #time6基本信息分组描述
describeBy(mice2$time8, group = mice2$group) #time8基本信息分组描述

分组绘制箱线图：

par(mfrow = c(1, 4))  #设置画1行3个图
boxplot(time2~group, mice2, xlab = expression("time2"))  #绘制T1箱线图
boxplot(time4~group, mice2, xlab = expression("time4"))  #绘制T2箱线图
boxplot(time6~group, mice2, xlab = expression("time6"))  #绘制T3箱线图
boxplot(time8~group, mice2, xlab = expression("time8"))  #绘制T3箱线图

describeBy (描述性分析)”结果中，列出了各组观察变量的最小值和最大值，依据专业尚不能认为存在异常值；此外，图4中的第1和第2个箱线图中分别存在一个离群值，但根据专业尚不能判定为异常值。综上，本案例未发现需要处理的异常值。

处理因素效应包含受试对象间变异中，重复测量因子效应和交互效应包含在受试对象内的变异中。对于处理组之间的比较，如果满足方差齐性的要求，可以采用普通方差分析的F检验。受试对象内的变异由于各观测值不独立，需考察两个时间点测量值之差的重提方差是否相等，也即是球形检验。如果球形检验不拒绝H0，则可以采用普通方差分析的F检验，反之，方差分析中需要对受试对象内效应的检验统计量F值得自由度进行校正，否则可能增大第一类错误的概率。自由度校正方法：用原始的分子和分母自由度分别乘以一个校正因子（0<1）。=1表示满足球形检验假设，越小说明偏离球形假设越严重。

正态性检验：

#第一种格式组内正态性检验
shapiro.test(mice$weight[time=="2"]) #P值0.2199
shapiro.test(mice$weight[time=="4"]) #P值0.157
shapiro.test(mice$weight[time=="6"]) #p值0.8676
shapiro.test(mice$weight[time=="8"]) #p值0.7656

#第二种格式的正态性检验
attach(mice2)
tapply(time2,group,shapiro.test) #检验time2的正态性 
tapply(time4,group,shapiro.test) #检验time4的正态性
tapply(time6,group,shapiro.test) #检验time6的正态性
tapply(time8,group,shapiro.test) #检验time8的正态性

该数据time4并不严格服从正态分布，QQ图基本满足正态性分布暂当作正态分布处理。

还可以使用Q-Q图进一步判断：

par(mfrow = c(1, 4))  #设置画1行4个图
qqnorm(time2, ylab="weight", main="T2")  #绘制T0组的qq图
qqline(time2)  #增加趋势线
qqnorm(time4, ylab="weight", main="T4")  #绘制T0组的qq图
qqline(time4)  #增加趋势线
qqnorm(time6, ylab="weight", main="T6")  #绘制T0组的qq图
qqline(time6)  #增加趋势线
qqnorm(time8, ylab="weight", main="T8")  #绘制T0组的qq图
qqline(time8)  #增加趋势线

方差齐性检验：

attach(mice)
food <- factor(food)
time <- factor(time)
number <- factor(number,ordered = F)
bartlett.test(weight~food,data=mice)
#或逐一每时间段内处理效应间的方差齐性检验
bartlett.test(time2~food,data=mice2)#p=0.338
bartlett.test(time4~food,data=mice2)#p=0.607
bartlett.test(time6~food,data=mice2)#p=0.7524
bartlett.test(time8~food,data=mice2)#p=0.5429

 P>0.1说明处理组满足方差分析的F检验

球形性检验：

如果要进行球形检验和后续的方差分析，则第二种格式的数据中数据进行转换为第一种格式：

宽数据转化为长数据（非常重要的技能）：

library(reshape2)  #调用包“reshape2”
mice2_long<-melt(data=mice2,id.vars=c('food','group',"number"), #保留不变的变量
                  measure.vars=c('time2','time6','time4',"time8"), #想要转换的变量
                  variable.name='time', #转换后的分类变量名
                  value.name='weight') #转换后的数值变量名

library(ez) #调用包“ez”
ezANOVA(data=mice2_long,
        dv=weight,wid=number,
        within=.(time),
        between=food,
        detailed=T) #重复测量方差分析
ezANOVA(data=mice,dv=weight,wid=number,within = .(time),between = food,detailed = T)

函数ezANOVA( data, dv, wid, within = NULL, within_full = NULL, within_covariates = NULL, between = NULL, between_covariates = NULL, observed = NULL, diff = NULL, reverse_diff = FALSE, type = 2, white.adjust = FALSE, detailed = FALSE, return_aov = FALSE )

dv：是结果变量/因变量，wid为个体标签也即是subject是实验对象的ID，within是重复测量因子，within, 数据集中的被试内自变量，如果只有一个时可以直接声明，有多变量的情况
下其格式为 within = .(FactorA, FactorB) *注意括号前面有个英文的句号，between处理因素。type, 默认的计算类型的II型，只考虑自变量的主效应，不考虑交互作用。如果数
据是平衡的，且不存在交互作用，则Type I，II和III得出的结果是相同的。detailed, 默认是FALSE，如果选择TRUE，则返回自变量的error及Sum squares（用
于后期计算）

第一个表ANOVA即方差分析的结果，其中ges（Generalized Eta-Squared）表示的。后面两个表依次为球形检验的结果及其校正。当球形检验的p 值大于0.05时，自变量各水平之间都符合球形假设，即相互独立。反之则表明不符合球形假设，需要参考第三个表Sphericity Corrections中的GGe（Greenhouse-Geisser epsilon）或者HFe（Huynh-Feldt epsilon）对df 进行校正。关于采取哪种校正方案， Girden (1992)认为当epsilon > 0.75时，建议用Huynh-Feldt校正，当epsilon < 0.75时，建议用Greenhouse-Geisser校正。

time效应和time:food交互效应的球形检验P=0.026<0.05，不满足球形检验，为此需要根据Sphericity Corrections 中的GGe对time和交互作用的自由度df 进行校正=0.5991872。

model <- ezANOVA(data=mice2_long,
                 dv=weight,wid=number,
                 within=.(time),
                 between=food,
                 detailed=T) #重复测量方差分析
model
time_DFn=3*model$`Sphericity Corrections`[1,2]
time_DFd=42*model$`Sphericity Corrections`[1,2]
food_time_DFn=3*model$`Sphericity Corrections`[2,2]
food_time_DFd=42*model$`Sphericity Corrections`[2,2]

计算出校正后time和交互项的自由度。

ezANOVA默认输出的是，但有些期刊要求报告，在多变量模型中表示排除其他变量后自变量对因变量单独的影响。根据的计算公式，我们将ANOVA列表中的SSn / SSn + SSd 即可得到的值（对应前文公式中提到的detailed）

model$ANOVA[4]/(model$ANOVA[4]+model$ANOVA[5])

重复测量方差分析：

1.上述的球形检验已经输出了方差分析的结果，food:time的交互F=5.12，p<0.05，提示time与food之间的交互作用有统计学意义，本案例需要分析单独效应。如果交互作用无统计学意义可直接，分析结果进行判断。

with(mice2_long, 
     interaction.plot(time, food, weight, 
                      type="b", col=c("red", "blue"),
                      las=2,
                      pch=c(16, 18), 
                      main="Interaction Plot for Food and Time"))

with（data，iteraction.plot(重复因子，处理变量，因变量）用图形方式展示重复测量的结果：

boxplot(weight ~ food*time, data = mice2_long, col = c("gold","green"),
        main = "两因素两水平重复测量方差分析")

单独效应：

#宽数据格式，如mice2
MANOVA(data=mice2,dvs=c("time2","time4","time6","time8"), dvs.pattern = "time(.)",
       between="food",within = "time") %>%
  EMMEANS("food",by="time") %>%
  EMMEANS("time",by="food")
#长数据格式，如mice，mice2_long
MANOVA(data=mice2_long,subID = "number",dv="weight",
       between="food",within = "time",sph.correction="GG") %>%
  EMMEANS("food",by="time") %>%
  EMMEANS("time",by="food")

MANOVA是多因素的方差分析函数，可以应用于长数据和宽数据。

宽数据：

1.个体间方差分析的设计：MANOVA(data=, dv=, between=, ...)；

2.个体内方差分析：MANOVA(data=, dvs=, dvs.pattern=, within=, ...)；

3.混合方差分析：MANOVA(data=, dvs=, dvs.pattern=, between=, within=, ...)

长数据：

混合方差分析：MANOVA(data=, subID=, dv=, between=, within=, ...)

data：支持长数据和宽数据格式的数据框；subID：受试对象ID；dv：结局变量；between：组间因素，即是处理因素；within：测量重复因子；只能宽数据dvs：重复测量因素，可以输入为向量或者time2:time8；dvs.pattern:重复测量因素的格式类型，eg：time(.)表示重复测量变量为time1，time2，time(..)表示time1a，timebb，time22，X(..)Y(.)表示X00Y0，X01Y2等

cov：具体的协变量；ss.type:SS方的计算类型；sph.correction自由度校正方法，球检验有意义时指定，包括“none”，“GG”，“HF”

！如果上述指标有多个因素可以使用向量组合，如within=c（“A”，“B”）

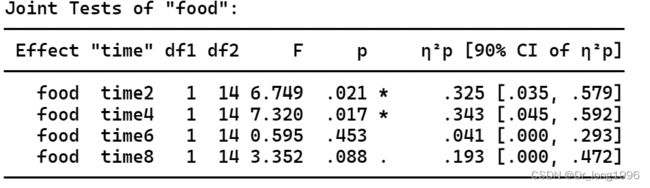
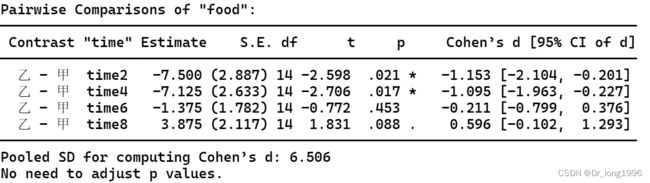
图 一：“Joint Tests of ‘time’ (time的单独效应)”可知，组内不同甲时间点的体重增量差异有统计学意义(F=4.738，P<0.05)；乙组内不同时间点的体重增量差异也有统计学意义(F=10.854，P<0.001)。

图二：为各组的“Mean (估算边际均值(偏最小二乘均值))”、“S.E. (标准误)”及均值的“95% Confidence Interval (95%CI)”。

 图三：各时间段组中两两比较结果。

同理饲料的单独效应结果如下：

案例二：因变量是二氧化碳吸收量（uptake），单位为ml/L，自变量是植物类型Type（魁北克VS.密西西比）和七种水平（95~1000 umol/m^2 sec）的二氧化碳浓度（conc）。另外， Type是组间因子， conc是组内因子。

data(CO2)
str(CO2)
attach(CO2)
conc <- factor(conc)
CO2.aov <- aov(uptake~Type*conc+Error(Plant/Type))
summary(CO2.aov)

所以不同种类的树吸收率有差别，不同浓度吸收率也有差异，且存在种类和浓度之间的交互。

        根据重复测量的方差分析公式aov（因变量~组间变量*组内变量+Error（subject/组内变量））subject是重复测量的样本的那一列值，也即是同一样本的标签组。组间和组内变量顺序不能弄错。

如果多个处理因素，则格式改为：

fit <- aov(y ~a*b*time +Error(s/time)) #a,b为处理因素，time为重复测量因子。
summary(fit)

随机区组设计方差分析

案例：为了研究A、B、C、D、E五种消毒液对细菌的抑制效果，用四种细菌在完全相同的培养条件下进行实验，每种细菌的5个培养皿分别随机选用一种消毒液。

mydata <- data.frame(细菌种类=c("大肠埃希菌","铜绿假单胞菌","葡萄球菌","痢疾杆菌"),
                     A=c(15,11,25,20),B=c(17,12,28,17),C=c(15,14,25,19),
                     D=c(14,13,30,13),E=c(12,9,20,11))
mydata

分析：消毒液是主要的处理因素，四种细菌分别为四个区组。整体的方差分析可以将总变异分为SS处理+SS区组+SS误差。

区组设计的条件：

• 条件1：观察变量唯一，且为连续变量。结局变量为抑菌圈直径大小，为连续性数值型变量
• 条件2：有两个因素，且都为分类变量。本研究中有处理效应(消毒液)及区组(细菌种类)两个因素，都为分类变量
• 条件3：观测值相互独立
• 条件4：相互比较的各处理水平(组别)的总体方差相等，即方差齐同，可采用方差齐性检验
• 条件5：各组、各水平观测值为正态(或近似正态)分布或因变量残差整体服从正态分布
• 条件6：观察变量不存在显著的异常值

#进行宽转长的操作
library(reshape2)
mydata_long <- melt(data=mydata,vars="细菌种类",
                    measure.vars = c("A","B","C","D","E"),
                    variable.name = "group",
                    value.name = "抑菌圈直径")
mydata_long
#对处理因素和区组因素进行因子化
mydata_long$group=factor(mydata_long$group)
mydata_long$细菌种类=factor(mydata_long$细菌种类)
str(mydata_long)

对适用条件进行评价：

1.生成残差，并整合到表格中

aov_mydata <- aov(抑菌圈直径~ 细菌种类 + group, mydata_long) #生成方差分析模型
summary(aov_mydata)
res <- rstandard(aov_mydata);res #提取标准化残差赋值给res
pre <- predict(aov_mydata);pre #提取预测值赋值给pre
mydata_long <- data.frame(mydata_long, res, pre) #重新形成数据集
View(mydata_long)  #查看数据

2.对各处理组之间的残差进行检验，评价方差齐性

library(car)
leveneTest(res~group,data=mydata_long)

 方差齐性检验后，p值为0.5266，提示各处理水平的总体方差相等。

3.正态性检验

tapply(mydata_long$res, mydata_long$group, shapiro.test) 

正态性检验结果。可知A，B，C、D、E五种消毒液的p值均>0.1，提示因变量残差整体服从正态分布。

4.异常值和检查极端值

library(ggplot2)#调用包“ggplot2”
boxp <- ggplot(mydata_long, aes(x = group, y = res))+ #定义颜色与分组
  stat_boxplot(geom = 'errorbar')+ #添加误差线
  geom_boxplot() #绘制箱线图
ggsave("boxp.png", width=8, height=5, dpi=300) #保存图片

 残差箱线图未见明显的异常值和极端值。

5.借助残差图分析随机区组设计变量是否满足方差分析的条件。

library(ggplot2)
a <- ggplot(data=mydata_long,aes(x=group,y=res,color=group))+
  geom_point()
b <- ggplot(data=mydata_long,aes(x=细菌种类,y=res,color=细菌种类))+
  geom_point()
c <- ggplot(data=mydata_long,aes(x=pre,y=res))+
  geom_point()
#ggplot不能使用par(mfrow(1,3))这样组合在一张图，需要使用cowplot包组合ggplot的图片
library(cowplot)
plot_grid(a,b,c,ncol=3)

 若散点随机在残差为0的横线上下，且无任何特殊的结构，不存在异常点，则可以认为符合防擦好分析的前提条件。

统计描述和假设检验：

library(psych) #调用包“psych”
describeBy(mydata_long$抑菌圈直径, group = mydata_long$group)

方差分析结果解读：

summary(aov_mydata)

 对处理因素的检验p=0.029，拒绝H0，可以认为五种消毒液的抑菌效果不全相同，各区组的p<0.001，可以认为对于同一种消毒液而言，不同细菌产生的反应不全相同。

使用线性回归模型来设置对照组进行比较：

blrfit = lm(抑菌圈直径~ 细菌种类 + group, data = mydata_long)
summary(blrfit)

默认第一个为对照组，也即是A消毒剂。与消毒剂A相比，消毒剂E的抑菌效果比A低4.75mm，差异有统计学意义（p=0.0124）。

mydata_long$group <- relevel(mydata_long$group, ref = "B") #将药物B设置为参照组
blrfit = lm(抑菌圈直径~ 细菌种类 + group, data = mydata_long)
summary(blrfit)

交叉设计方差分析

案例：为研究两种环孢素微乳化口服溶液在健康人体中得药动学及生物学特性，采用两阶段得交叉设计方案。将20名志愿者按照体重编号随机分成甲乙两组，甲组I阶段口服环孢素微乳化溶液供试500制剂（T）500mg，经过一周得洗脱期后，II阶段服用环孢素乳化液参比制剂（C）500mg，乙组先口服C，在口服T，观测指标为血药浓度-时间曲线下面积（AUC）。

mydata=data.frame(ID=rep(1:20,2),
                  drug=c("T","T","C","T","C","T","C","T","C","C","C","T","C","C","T","T","C","T","T","C",
                         "C","C","T","C","T","C","T","C","T","T","T","C","T","T","C","C","T","C","C","T"),
                  stage=c(rep("I阶段",20),rep("II阶段",20)),
                  AUC=c(17.54,15.88,20.97,18.51,19.94,16.41,17.57,15.87,13.94,15.29,
                        15.81,16.11,17.42,15.92,14.09,15.95,17.00,15.29,16.46,17.86,
                        17.17,14.31,19.61,21.56,22.14,13.18,17.49,15.15,13.49,16.19,
                        15.78,15.14,15.95,14.43,16.22,13.93,14.02,11.97,14.11,13.27))
mydata
mydata$ID <- factor(mydata$ID)
mydata$drug <- factor(mydata$drug)
mydata$stage <- factor(mydata$stage)

基本的方差齐性和正态性检验同上：

方差分析：

library(psych)
describeBy(AUC~drug+stage,data=mydata)
describeBy(AUC~drug,data=mydata)
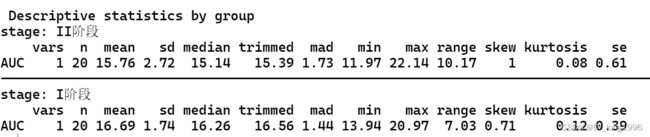
describeBy(AUC~stage,data=mydata)

 第一阶段T、C药物组的AUC分别为16.21±1.19、17.17±2.11，第二阶段C、T药物组的血浆浓度分别为15.27±2.65、16.24±2.84。

C 、T药物组总体AUC分别为16.22±2.53、16.22±2.12。

第一阶段、第二阶段总体的AUC分别为15.76±2.72、16.69±1.74。

aov_mydata <- aov(AUC~ID+drug+stage,data=mydata)
summary(aov_mydata)

格式：结局变量~观测对象编号+处理因素+阶段

 两阶段交叉设计的方差分析结果。drug的F=0.00，P=0.99826；表明尚不能认为两种药物AUC存在差异。stage的F=4.293，P=0.05292，表明尚不能两阶段AUC有统计学意义。ID的F=4.167，P<0.001，表明个体间AUC差异有统计学意义。

析因设计变量的方差分析

案例：某医生欲研究A、B两种新药对高胆固醇血症患者是否有降低胆固醇的作用，已经两药是否存在交互效应。按照纳入标准选择了20名高胆固醇患者，随机分成了甲乙丙丁4组，每组5例。甲组作为对照组，AB药都不用，乙组只用A药物，丙组只用B药物，丁组A、B药物同时使用，分别测量每位患者胆固醇降低值。

mydata=data.frame(chol=c(0.8565,0.7352,0.9357,1.2698,0.9217,1.1365,1.1025,1.4213,1.1876,1.1564,
                         1.1532,0.9918,1.2121,0.9857,0.8832,1.7862,2.0123,2.3242,1.9892,2.0012),
                  DrugA=c(rep("A1",5),rep("A2",5),rep("A1",5),rep("A2",5)),
                  DrugB=c(rep("B1",10),rep("B2",10)))
mydata
str(mydata)
#对变量进行因子化
mydata$DrugA=factor(mydata$DrugA,levels = c("A1","A2"),labels = c("不用A药（A1）","用A药（A2）"))
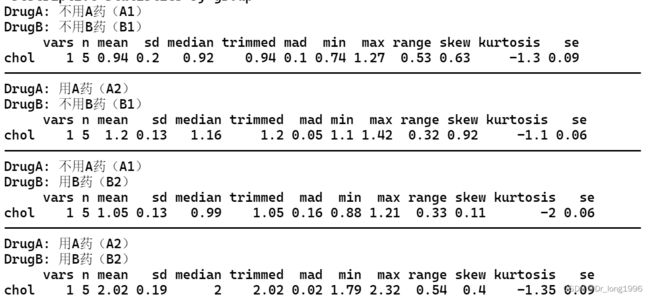
mydata$DrugB=factor(mydata$DrugB,levels = c("B1","B2"),labels = c("不用B药（B1）","用B药（B2）"))

统计描述：查看四个组中胆固醇下降值得平均值

library(psych)
describeBy(chol~DrugA+DrugB,data=mydata)
#或者
#install.packages("compareGroups")
library(compareGroups)
strataTable(descrTable(DrugA~chol,data=mydata),"DrugB")
strataTable(descrTable(DrugB~chol,data=mydata),"DrugA")

 单独效应：指其他因素水平固定时，同一因素不同水平的效应之差。

不用B药的情况下，用A药的单独效应为：1.20-0.94=0.22

用B药的情况下，用A药的单独效应为：2.02-1.05=0.97

不用A药的情况下，用B药的单独效应为：1.05-0.94=0.11

用A药的情况下，用B药的单独效应为：2.02-1.20=0.82

主效应：指某一因素单独效应的平均值。

在本例中，胆固醇降低情况在A1和A2，使用B药的单独效为0.11，0.82，因此B药的主效应为（0.11+0.82）/2=0.465。同理A药的主效应为(0.22+0.97)/2=0.595

交互效用是指两因素或多因素间效应互不独立的情况下，当某一因素在各水平间变化时，另一（多）个因素各水平的效应也相应地发生变化。

AB两因素的交互作用计算公式为：

AB交互效应=1/2(A1时B的单独效应—A2时B的单独效应）=1/2(B1时A的单独效应—B2时A的单独效应）

AB两药物的交互效应=(0.82-0.11)/2=(0.97-0.22)/2=0.355

假设检验：

假设存在交互作用，进行方差分析：

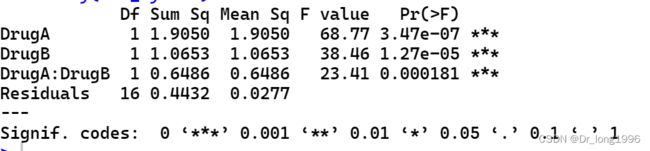
aov_mydata<-aov(chol~DrugA*DrugB,data=mydata)
summary(aov_mydata)

 DrugA的主效应(p<0.001）,DrugB的主效应(p<0.001），表示他们对胆固醇降低均有影响，两者交互作用(p<0.001)对胆固醇降低也存在显著影响。

！！！！如果在确定无交互效应时我们可以构建无交互项的模型

aov_mydata2 <- aov(chol~DrugA+DrugB,data=mydata)
summary(aov_mydata2)

接下来我们看看每个因素对胆固醇水平的具体影响

A药对胆固醇的影响：

TukeyHSD(aov_mydata,"DrugA")

 用A药对降低胆固醇是有影响的。通理，B药如下：

TukeyHSD(aov_mydata,"DrugB")

2.5 多元方差分析

多元：是指结果变量存在多个因素。

比如：将某肝炎病人随机分成两组，一组施以新的疗法，另一组仍用传统的治疗方法，考察用二种方法治疗后对反映病人肝功能指标（如SGPT、 AST 、 ALT、 HCV等）的影响。肝功能指标存在多种同时相互之间可能存在某种相关性。

思想：一个反应变量的方差分析都是对组间均方与组内均方进行比较，而前者是对组间方差协方差矩阵与组内方差协方差矩阵进行比较。

多元方差的条件：

• 各因变量服从多元正态分布
• 各观察对象之间相互独立
• 各组观察对象反应变量的方差-协方差矩阵相等
• 反应变量之间的确存在一定的关系，需要从专业或者研究目的角度判断

案例：以MASS包中的UScereal数据集：美国谷物中的卡路里、脂肪和糖含量是否会因为储存架位置的不同而发生变化；其中1代表底层货架， 2代表中层货架， 3代表顶层货架。卡路里、脂肪和糖含量是因变量，货架是三水平（1、 2、 3）的自变量。

library(MASS)
data("UScereal")
attach(UScereal)
shelf <- factor(shelf)
y <- cbind(calories, fat, sugars) #cbind()函数将三个因变量（卡路里、脂肪和糖）合并成一个矩阵。
aggregate(y, by=list(shelf), FUN=mean)
cov(y) #cov()则输出各谷物间的方差和协方差。
fit <- manova(y ~ shelf)
summary(fit)
summary.aov(fit) #由于多元检验是显著的，可以使用summary.aov()函数对每一个变量做单因素方差分析

因变量多元正态性（Q-Q图）：

center <- colMeans(y)
center
n <- nrow(y);n
p <- ncol(y);p
cov <- cov(y);cov
d <- mahalanobis(y,center,cov);d
coord <- qqplot(qchisq(ppoints(n),df=p),
                d, main="QQ Plot Assessing Multivariate Normality",
                ylab="Mahalanobis D2")
abline(a=0,b=1)

Q理论：若有一个p×1的多元正态随机向量x，均值为μ，协方差矩阵为Σ，那么x与μ的马氏距离的平方服从自由度为p的卡方分布。 Q-Q图展示卡方分布的分位数，横纵坐标分别是样本量与马氏距离平方值。如果点全部落在斜率为1、截距项为0的直线上，则表明数据服从多元正态分布。

若数据服从多元正态分布，那么点将落在直线上。还可以使用mvoutlier包中的ap.plot()函数来检验多元离群点。

library(mvoutlier)
outliers <- aq.plot(y)
outliers

当不满足多元方差分析条件时：

如果多元正态性或者方差 协方差均值假设都不满足或者你担心多元离群点，那么可以考虑用稳健或非参数版本的MANOVA 检验。稳健单因素MANOVA 可通过rrcov 包中的Wilks.test()函数实现。 vegan包中的adonis()函数则提供了非参数MANOVA的等同形式

library(rrcov)
Wilks.test(y,shelf, method="mcd")  

2.6 非参数检验

如果无法满足ANOVA设计的假设，那么可以使用非参数方法来评估组间的差异。如果各组独立，则Kruskal-Wallis检验将是一种实用的方法。如果各组不独立（如重复测量设计或随机区组设计），那么Friedman检验会更合适。

2.6.1 Kruskal-Wallis检验的调用格式为： kruskal.test(y ~ A, data)

 其中的y是一个数值型结果变量， A是一个拥有两个或更多水平的分组变量（若有两个水平，则它与Mann-Whitney U检验等价）。以胆固醇数据集为例：

library(multcomp)
data(cholesterol)
table(trt)   
## Kruskal-Wallis H检验 ##
library(coin)  #调用包“coin”
kruskal.test(cholesterol$response, cholesterol$trt)  #Kruskal-Wallis检验
kruskal.test(response~trt,data=cholesterol)#两种格式都可

事后两两比较：

## 事后两两比较 ##
library(PMCMR)  #调用程序包“PMCMR”
library(PMCMRplus)  #调用程序包“PMCMRplus”
kwAllPairsNemenyiTest(response~trt,data=cholesterol)#事后检验

2.6.2 Friedman检验的调用格式为： friedman.test(y ~ A | B, data)

 其中的y是数值型结果变量， A是一个分组变量，而B是一个用以认定匹配观测的区组变量（blocking variable）。在以上两例中， data皆为可选参数，它指定了包含这些变量的矩阵或数据框。

案例：8名受试对象在相同试验条件下分别接受A、B、C 3种不同频率振动的刺激，测量其反应率(%)，问3种频率振动刺激的反应率是否有差别？该研究为三个变量的配对实验，存在配对，所以首先考虑Fredman检验。

mydata <- data.frame(ID=c(1:8),
                     A=c(8.5,11.4,9.4,9.0,8.0,8.6,8.9,7.8),
                     B=c(9.6,12.7,9.1,8.7,8.0,9.8,9.0,8.2),
                     C=c(9.8,11.6,10.1,9.6,8.6,9.6,10.4,8.9))
str(mydata)

正态性检验：（1）QQ图（2）正态性检验

## 绘制Q-Q图 ##
par(mfrow = c(1, 3))  #设置画1行3个图片
qqnorm(mydata$A, main="A")  #绘制A的qq图
qqline(mydata$A)  #增加趋势线
qqnorm(mydata$B, main="B")  #绘制B的qq图
qqline(mydata$B)  #增加趋势线
qqnorm(mydata$C, main="C")  #绘制C的qq图
qqline(mydata$C)  #增加趋势线

## 正态性检验 ##
shapiro.test(mydata$A)  # A的shapiro-Wilk正态性检验
shapiro.test(mydata$B)  # B的shapiro-Wilk正态性检验
shapiro.test(mydata$C)  # C的shapiro-Wilk正态性检验

 Q-Q图上三组散点偏离对角线较远，尤其是A、B两组数据，提示三组数据不服从正态分布；图4的正态性检验结果显示A、B、C三组的P值分别为0.05988、0.03698和0.5969，前两组P值均<0.1，也提示两组数据不满足正态性条件。因此，本案例应使用Friedman检验比较三组反应率的差异。

## 统计推断 ##
#宽数据的处理
mydata2<-as.matrix(mydata)  #数据转换为矩阵格式
mydata3<-mydata2[,c(2,3,4)]  #去除第一列无用数据
friedman.test(mydata3)  #friedman检验

#长数据的处理
library(reshape2)#宽转长的操作
mydata_long <- melt(data=mydata,vars="ID",
                    measure.vars = c("A","B","C"),
                    variable.name = "group",
                    value.name = "response")
friedman.test (response~group|ID,data=mydata_long)
#格式为（因变量~分组变量|区组变量或者配对变量，data=数据名称）
library(PMCMR)
frdAllPairsNemenyiTest(response~group|ID,data=mydata_long)#事后两两比较