“快速排序:一种美丽的算法混沌”
欢迎来到我的博客!在今天的文章中,我将采用一种独特且直观的方式来探讨我们的主题:我会使用一幅图像来贯穿整篇文章的讲解。这幅精心设计的图表不仅是我们讨论的核心,也是一个视觉辅助工具,帮助你更深入地理解和掌握本文的内容。
通过这种方式,我们可以一步步深入本文的主题,每个阶段都将图像作为参考。这样不仅可以增加信息的吸收和理解,还能让学习过程更加生动和有趣。无论你是刚入门的新手还是寻求更深层次理解的老手,这幅图都将是你理解本文内容的有力工具。
所以,让我们开始这一独特的旅程,一边阅读文章,一边参考这幅将贯穿全文的图表,深入探索我们今天的话题!
想象一下,你走进了一个充满了成千上万本书的巨大图书馆。这些书籍横七竖八地堆放着,没有任何顺序。你需要找到一本特定的书,但在这混乱中,这看似是一个不可能完成的任务。这时,一位图书管理员出现了。这位管理员不仅知道每本书的具体位置,而且还能以令人难以置信的速度将这些书籍分类和组织起来,让你轻松地找到所需的书籍。这正是快速排序算法在数据世界中的角色:一个高效、精准的“信息管理员”,能迅速将数据整理成有序的结构。
快速排序,这个由英国计算机科学家Tony Hoare在1960年发明的算法,至今仍是计算机科学中最受欢迎和广泛使用的排序算法之一。它之所以名为“快速”,是因为它比其他传统排序算法(如冒泡排序或插入排序)要快得多,尤其是在处理大量数据时。快速排序的基本思想是选择一个元素作为“基准”,然后将数组分为两部分,一边是小于基准的元素,另一边是大于基准的元素,接着递归地在这两部分进行同样的操作。
在现代计算的世界里,快速排序不仅是一个算法的范例,它也是处理大规模数据不可或缺的工具。从数据库的查询优化到大数据分析,再到我们日常使用的搜索引擎,快速排序的影响无处不在。它的效率和优雅使它成为了计算机科学中的一个经典,一个在不断变化和发展的数字时代依然屹立不倒的算法巨人。
快速排序有四种方法。他们分别是“hoare版本” “挖坑法” 和 “前后指针版本” 和“非递归模拟实现”
1.hoare版本
一张图片带你秒懂过程!
快速排序的基本原理
快速排序是一种高效的排序算法,使用分而治之的策略来排序数据。以下是它的基本步骤:
-
选择基准值(Pivot):
从数组中选择一个元素作为基准值。这个选择可以是随机的,通常选择第一个或最后一个元素。 -
分区(Partitioning):
重新排列数组,使得所有小于基准值的元素都排在基准之前,而所有大于基准值的元素都排在基准之后。这个步骤结束后,基准元素就处于其最终位置。 -
递归排序子数组:
对基准左侧和右侧的子数组分别递归地执行快速排序。 -
终止条件:
当子数组的大小减至1或0时,递归结束,因为每个元素都已经被排序。
// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{
if(right - left <= 1)
return;
// 按照基准值对array数组的 [left, right)区间中的元素进行划分
int div = partion(array, left, right);
// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)
// 递归排[left, div)
QuickSort(array, left, div);
// 递归排[div+1, right)
QuickSort(array, div+1, right);
}上述为快速排序递归实现的主框架。
分区(Partitioning)
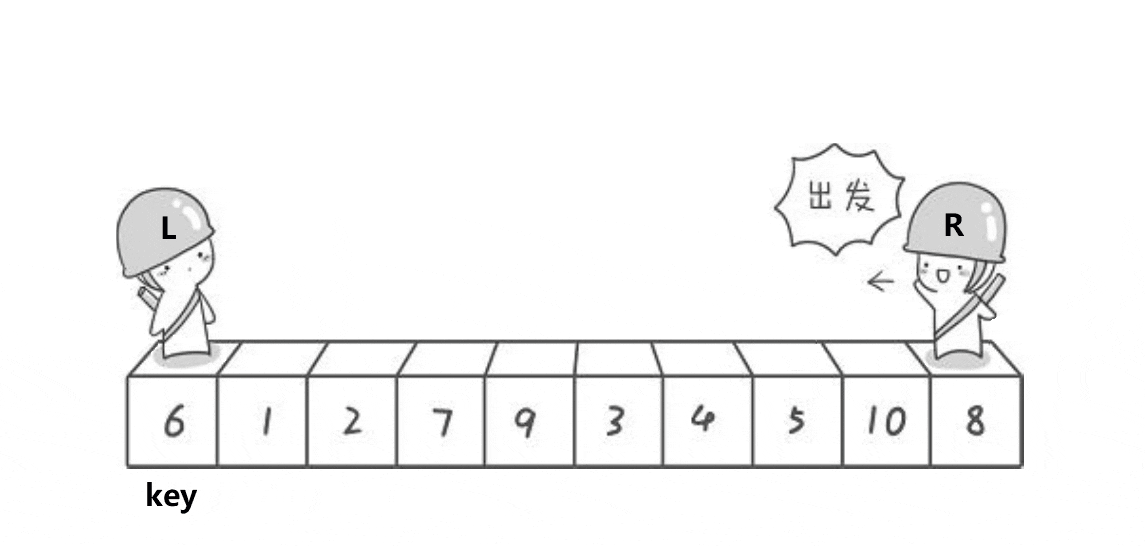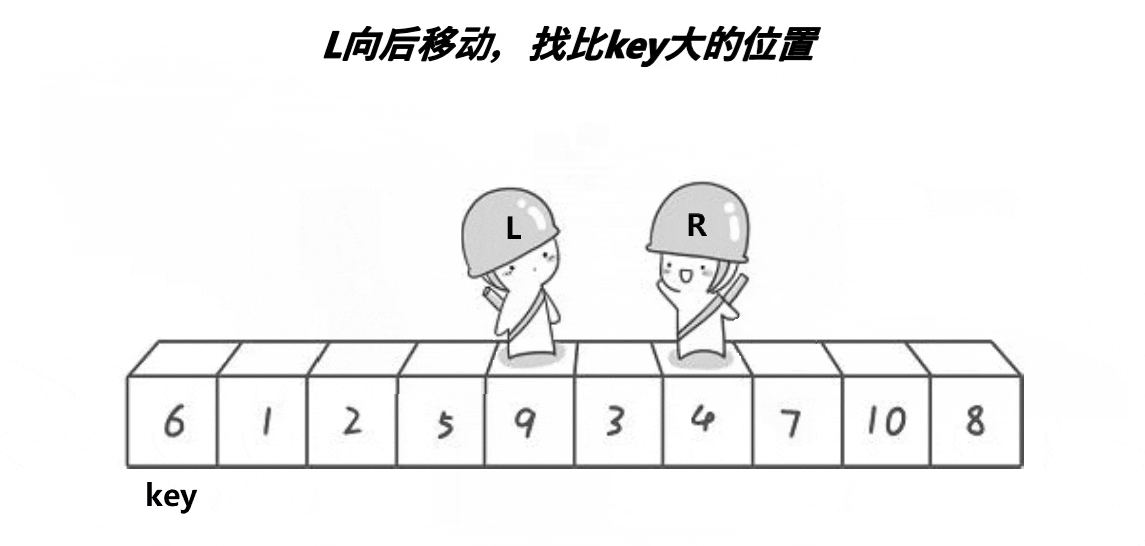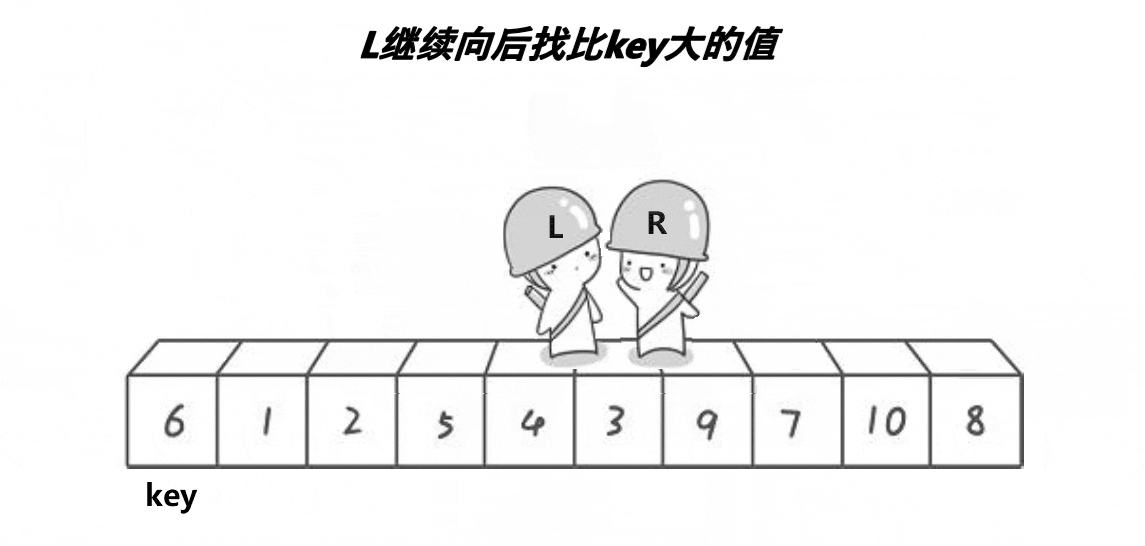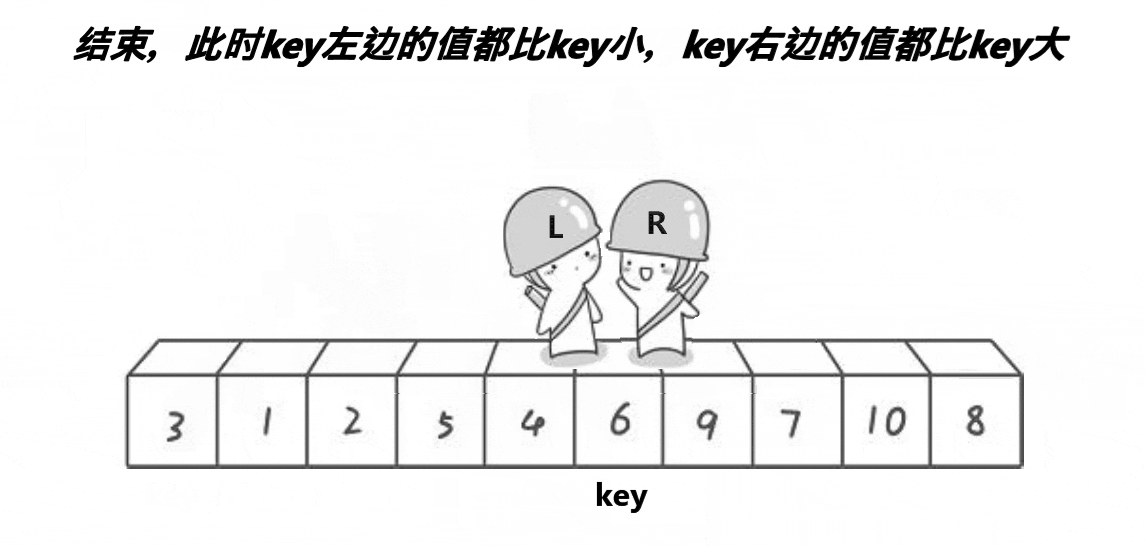
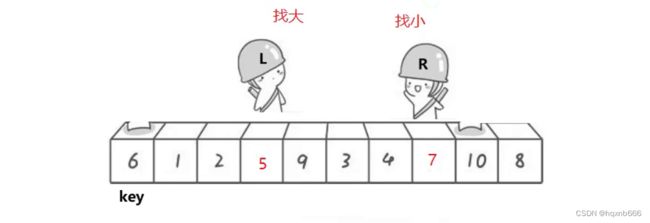
我们首先选择基准值将其定义为key 一般为最左或最右,此时,对其进行遍历,L向右找比key大的值,R向左找比key小的值,找到了就相互交换, 直到第一次相遇,将key与相遇点进行交换
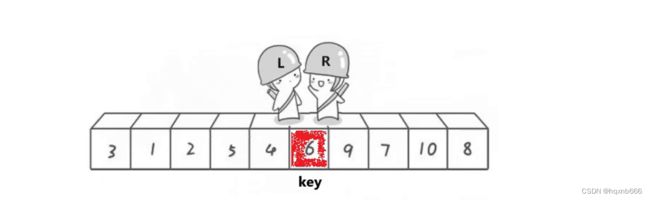
此时可能会有人疑问,为什么相遇就一定要交换,如果我们相遇后这个值比key大的情况下,是否违背我们要排序的初衷呢? 这里先给出答案:相遇位置一定比key小。
接下来我们实现初步代码,如何让他先进行左右交换并让key挪动到相遇位置
void QuickSort(int* a, int begin, int end)
{
int keyi = begin;
int right = end;
int left = begin ;
while (left < right)
{
//左边找大
while(left < right && a[left] < a[keyi])//加入&&的原因是如果到相遇点时,left还是小于kei,他不会在相遇点停下,并且再次交换就颠倒顺序了
{
++left;
}
//右边找小
while (left < right && a[right] < a[keyi])
{
--right;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
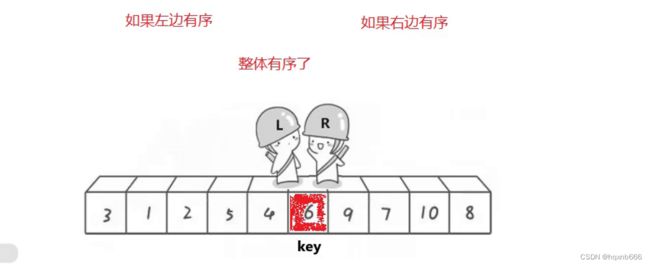
}那我们是不是可以得出,如果接下来让左边变得有序,右边也有序。整体就有序了
递归排序子数组
接下来我们对左右子数组进行递归处理,就可以得出一个有序数组
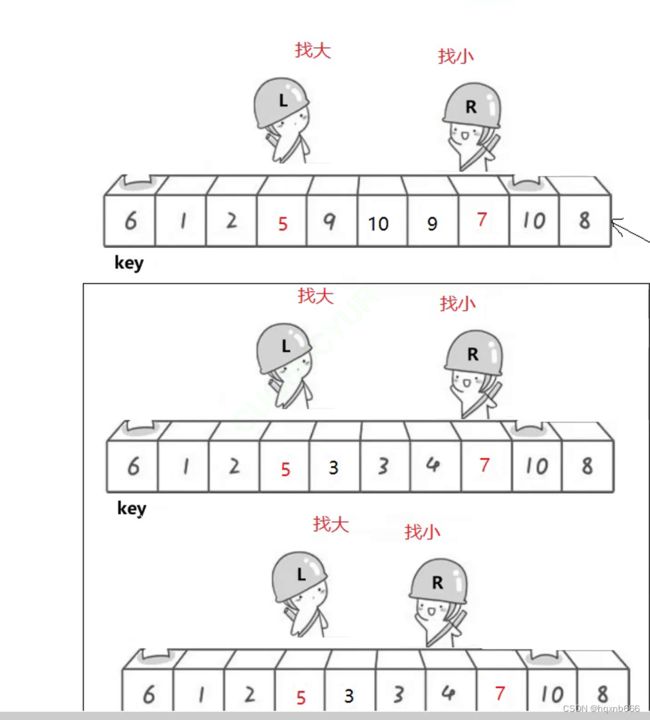
接下来我们先对左子树进行递归
进行处理后,3就是key就是相遇处,接着再对左子数组进行处理递归处理直到只剩一个数组时返回
接着再对右子树进行处理,以此类推,这里不多做赘述
终止条件
这里涉及到递归子分治问题,所以我们进行修改代码,将第一步的key也就是图中的6保留,keyi-1就是左边的数组个数,keyi+1就是右边的数组个数,我们进行递归,返回条件就是只有一个节点时返回。
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
int keyi = begin;
int right = end;
int left = begin+1 ;
while (left < right)
{
//左边找大
while(left < right && a[left] < a[keyi])//加入&&的原因是如果到相遇点时,left还是小于kei,他不会在相遇点停下,并且再次交换就颠倒顺序了
{
++left;
}
//右边找小
while (left < right && a[right] < a[keyi])
{
--right;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
//左半 [begin , keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}快速排序的优化
对以上代码进行测试,我们会发现在处理有序数组时,快速排序反而是最慢的排序
为什么有序的情况下快排会很吃亏呢? 因为我们采取了固定选Key
理想状态下,快排时间复杂度是O(N*logN)
所以我们采取三数取中法 可以避开所有最坏的情况,越接近二分,就越快
三数取中法是快速排序算法中一种改进的基准(pivot)选择方法。它的目的是减少快速排序在最坏情况下的时间复杂度,这通常发生在选择的基准值是最小或最大元素时。通过选择一个更接近中间值的基准,可以提高分区的均匀性,从而使算法更加高效。
在传统的快速排序中,基准通常被选择为数组的第一个元素、最后一个元素或随机一个元素,这样在面对某些特定的数据集时(比如已经排序或接近排序的数组)可能会导致算法效率低下。
三数取中法是通过考虑数组的第一个元素、中间元素和最后一个元素,然后选择这三个元素的中位数作为基准。这种方法在实践中通常能给出一个较好的基准,从而使得分区更加平衡。
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
int midi = GetMidi(a, begin, end);
Swap(&a[midi], &a[begin]);
int keyi = begin;
int right = end;
int left = begin ;
while (left < right)
{
//右边找小
while (left < right && a[right] >= a[keyi])
{
--right;
}
//左边找大
while(left < right && a[left] <= a[keyi])//加入&&的原因是如果到相遇点时,left还是小于kei,他不会在相遇点停下,并且再次交换就颠倒顺序了
{
++left;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
//左半 [begin , keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}-
begin 和 end: 这两个变量通常表示正在处理的数组或子数组的开始和结束索引。在数组的第一次排序时,
begin通常是 0(数组的第一个元素的索引),而end是数组的最后一个元素的索引。 -
计算中点:
(begin + end) / 2这个表达式的目的是找到begin和end之间的中间索引。这是通过将begin和end的值相加,然后除以 2 来实现的。由于这里使用的是整数除法,所以即使begin + end是奇数,结果也会被自动向下取整到最接近的整数。 -
数组索引: 在 C/C++ 中,数组的索引是从 0 开始的。因此,计算出的
midi一定是一个有效的数组索引,只要begin和end是有效的。这意味着a[midi]是数组中的一个实际元素。
总结来说,int midi = (begin + end) / 2; 确保 midi 是位于 begin 和 end 之间的一个有效索引,而 a[midi] 则是数组在这个索引位置的元素。这是一种常见的找到数组中间元素索引的方法。
结论:Hoare版本快速排序的效率与优势
Hoare版本的快速排序算法是计算机科学中的一个经典例子,它展示了高效算法设计的重要性。通过其独特的分区策略,该算法能够快速、高效地处理各种大小的数据集。Hoare版本的快速排序在最佳情况下的时间复杂度为 O(n log n),并且即使在平均情况下也能维持这一高效表现。虽然它在最坏情况下的时间复杂度为 O(n^2),但通过智能选择枢轴点,如使用三数取中法或随机选取,可以大幅减少这一风险。
此外,Hoare版本相较于其他变体如Lomuto分区方法,通常需要更少的数据交换操作,这使得它在处理大数据集时更为高效。然而,它的实现相比一些其他版本更为复杂,可能需要更细致的理解和调试。
总的来说,Hoare版本的快速排序因其高效性和对大数据集友好的特性,在算法领域和实际应用中仍然占有一席之地。它不仅是排序算法的一个优秀代表,也是计算机算法设计和分析的一个经典案例。
2.“挖坑法”
什么是挖坑法?
挖坑法是快速排序的一种实现方式,它的核心思想是将数组分为两部分,使得一部分的所有元素都比另一部分的元素小。这个过程通过“挖坑”和“填坑”来实现,即在数组中创建一个“坑”,并用合适的元素填补它。
int PartSort2(int* a, int begin, int end)
{
int midi = GetMidi(a, begin, end);
Swap(&a[midi], &a[begin]);
int key = a[begin];
int hole = begin;
while (begin < end)
{
//右边找小,找左边的坑
while (begin < end && a[end] >= key)
{
end--;
}
a[hole] = a[end];
hole = end;
// 左边找大,填到右边的坑
while (begin < end && a[begin] <= key)
{
++begin;
}
a[hole] = a[begin];
hole = begin;
}
a[hole] = key;
return hole;
}void QuickSort2(int* a, int begin, int end)
{
if (begin >= end)
return;
if (end - begin + 1 <= 10) //小区间优化
{
InsertSort(a + begin, end - begin + 1); //a+begin 防止都是从左数组开始
}
int keyi = PartSort2(a, begin, end);
QuickSort2(a, begin, keyi - 1);
QuickSort2(a, keyi + 1, end);
}挖坑法的优点
- 效率高:通过选取合适的基准值,挖坑法能够有效减少不必要的数据交换,从而提高排序效率。
- 易于理解:这种方法的逻辑清晰,易于理解和实现。
- 适用范围广:适用于大多数需要排序的场景,尤其是数据量较大的情况。
结语
快速排序的挖坑法不仅效率高,且易于理解和实现。通过上述代码示例,我们可以清晰地看到其具体实现过程和方法。无论是学习算法还是解决实际问题,掌握这种排序方法都是非常有价值的。
3.前后指针法
什么是前后指针法?
前后指针法是快速排序的一种实现技巧,它使用两个指针在数组中从前往后遍历,以此来重新排列元素,达到排序的目的。该方法通过将数组分成两部分,其中一部分的所有元素都比另一部分的元素小来实现排序。
int PartSort3(int* a, int begin, int end)
{
int midi = GetMidi(a, begin, end);
Swap(&a[midi], &a[begin]);
int keyi = begin;
int prev = begin;
int cur = prev + 1;
while (cur<=end)
{
if(a[cur] < a[keyi] && ++prev != cur)
Swap(&a[prev], &a[cur]);
++cur;
}
Swap(&a[keyi], &a[prev]);
keyi = prev;
return keyi;
}
void QuickSort3(int* a, int begin, int end)
{
if (begin >= end)
return;
if (end - begin + 1 <= 10) //小区间优化
{
InsertSort(a + begin, end - begin + 1); //a+begin 防止都是从左数组开始
}
int keyi = PartSort3(a, begin, end);
QuickSort3(a, begin, keyi - 1);
QuickSort3(a, keyi + 1, end);
}前后指针法的优点
- 高效:前后指针法减少了不必要的数据交换,提高了排序效率。
- 易理解:该方法的逻辑清晰,易于理解和编写。
- 广泛适用:适用于多种排序场景,特别是数据量较大的情况。
结语
快速排序的前后指针法提供了一个高效且易于理解的排序策略。通过上述的代码示例,我们可以清楚地看到其具体的实现方法。无论是在学术学习还是实际编程中,掌握这种排序技巧都将非常有益。
4非递归实现快速排序:栈的应用
快速排序是一种高效的排序算法,通常以递归的形式实现。然而,在某些情况下,递归可能导致栈溢出或额外的性能开销。为了解决这些问题,可以使用非递归的方式来实现快速排序,本文将通过一个具体的栈结构实现的示例来详细介绍这种方法。
为什么使用非递归快速排序?
非递归快速排序的主要优势在于它避免了递归带来的栈溢出风险,特别是在处理大数据集时。此外,非递归实现在某些情况下可能更加高效,因为它减少了函数调用的开销。
void QuickSortNonR(int* a, int begin, int end)
{
ST s;
STInit(&s);
STPush(&s, end);
STPush(&s, begin);
while (!STEmpty(&s))
{
int left = STTop(&s);
STPop(&s);
int right = STTop(&s);
STPop(&s);
int keyi = PartSort3(a, left, right);
// [left, keyi-1] keyi [keyi+1,right]
if (left < keyi - 1)
{
STPush(&s, keyi - 1);
STPush(&s, left);
}
if (keyi + 1 < right)
{
STPush(&s, right);
STPush(&s, keyi+1);
}
}
STDestory(&s);
}非递归快速排序的优势
- 避免栈溢出:在处理大数据集时,递归可能会导致栈溢出。非递归实现避免了这个问题。
- 性能提升:在某些情况下,非递归实现由于减少了函数调用,可能会有更好的性能表现。
结语
非递归快速排序提供了一种有效的替代方案,特别是在处理大规模数据时。通过使用栈结构来模拟递归过程,我们不仅可以避免潜在的栈溢出问题,还可能获得性能上的提升。掌握这种方法,对于深入理解快速排序算法和处理大数据集具有重要意义。