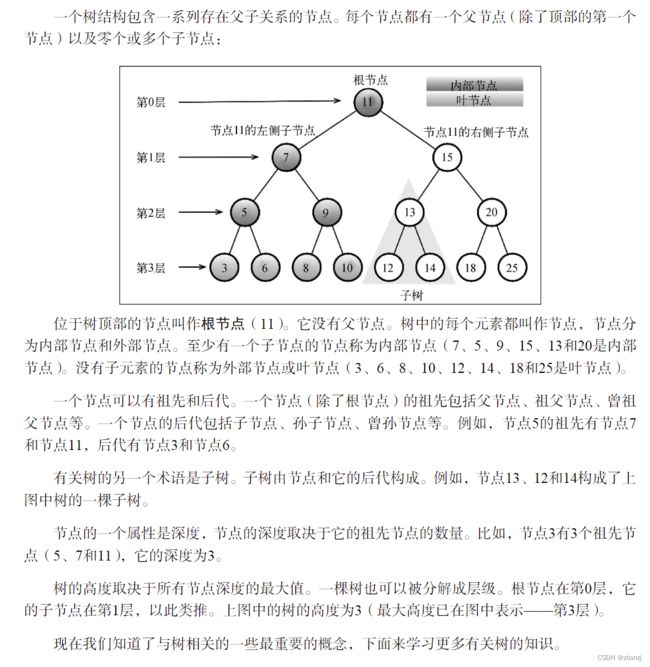
第七章 树
7.1 树数据结构
树是一种分层数据的抽象模型。现实生活中最常见的树的例子是家谱,或是公司的组织架构
图,如下图所示: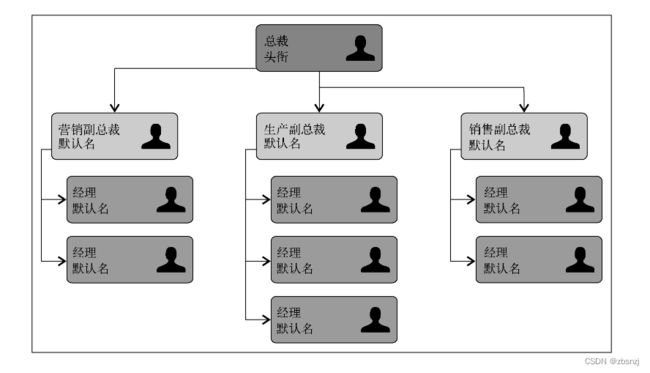
7.2 树的相关术语
7.3 二叉树和二叉搜索树
二叉树中的节点最多只能有两个子节点:一个是左侧子节点,另一个是右侧子节点。这些定义有助于我们写出更高效的向/从树中插入、查找和删除节点的算法。二叉树在计算机科学中的
应用非常广泛。
二叉搜索树(BST)是二叉树的一种,但是它只允许你在左侧节点存储(比父节点)小的值,在右侧节点存储(比父节点)大(或者等于)的值。上一节的图中就展现了一棵二叉搜索树。
7.3.1 创建BinarySearchTree类
function BinarySearchTree(){
var Node = function(key){ // {1}
this.key = key
this.left = null
this.right = null
}
var root = null // {2}
} 和链表一样,将通过指针来表示节点之间的关系(术语称其为边)。在双向链表中,每个节
点包含两个指针,一个指向下一个节点,另一个指向上一个节点。对于树,使用同样的方式(也
使用两个指针)。但是,一个指向左侧子节点,另一个指向右侧子节点。因此,将声明一个Node
类来表示树中的每个节点(行{1})。值得注意的一个小细节是,不同于在之前的章节中将节点
本身称作节点或项,我们将会称其为键。键是树相关的术语中对节点的称呼。
我们将会遵循和LinkedList类中相同的模式(第4章),这表示也将声明一个变量以控制此数据结构的第一个节点。在树中,它不再是头节点,而是根元素(行{2})。然后,我们需要实现一些方法。下面是将要在树类中实现的方法。
insert(key):向树中插入一个新的键。
search(key):在树中查找一个键,如果节点存在,则返回true;如果不存在,则返回false。
inOrderTraverse:通过中序遍历方式遍历所有节点。
preOrderTraverse:通过先序遍历方式遍历所有节点。
postOrderTraverse:通过后序遍历方式遍历所有节点。
min:返回树中最小的值/键。
max:返回树中最大的值/键。
remove(key):从树中移除某个键。
7.3.2 向树中插入一个键
this.insert = function(key){
var newNode = new Node(key)
if(root === null){
root=newNode
}else{
insertNode(root,newNode)
}
} 要向树中插入一个新的节点(或项),要经历三个步骤。
第一步是创建用来表示新节点的Node类实例(行{1})。只需要向构造函数传递我们想用来插入树的节点值,它的左指针和右指针的值会由构造函数自动设置为null。
第二步要验证这个插入操作是否为一种特殊情况。这个特殊情况就是我们要插入的节点是树
的第一个节点(行{2})。如果是,就将根节点指向新节点。
第三步是将节点加在非根节点的其他位置。这种情况下,需要一个私有的辅助函数({3}),
函数定义如下:
var insertNode = function(node,newNode){
if(newNode.key 如果树非空,需要找到插入新节点的位置。因此,在调用insertNode方法时要通过参数传入树的根节点和要插入的节点。
如果新节点的键小于当前节点的键(现在,当前节点就是根节点)(行{4}),那么需要检查当前节点的左侧子节点。如果它没有左侧子节点(行{5}),就在那里插入新的节点。如果有左侧子节点,需要通过递归调用insertNode方法(行{7})继续找到树的下一层。在这里,下次将要比较的节点将会是当前节点的左侧子节点。
如果节点的键比当前节点的键大,同时当前节点没有右侧子节点(行{8}),就在那里插入新的节点(行{9})。如果有右侧子节点,同样需要递归调用insertNode方法,但是要用来和新节点比较的节点将会是右侧子节点。
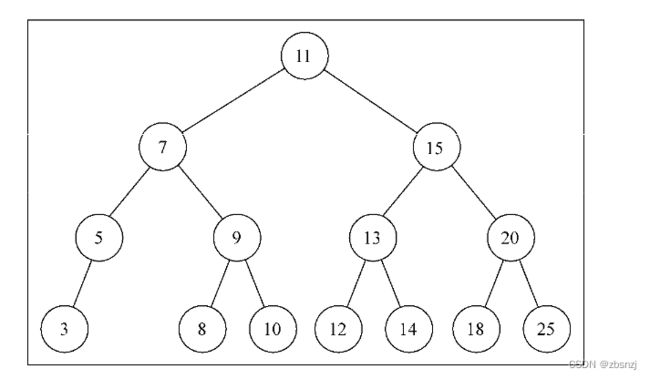
假如已经创建了如下所示的树结构:
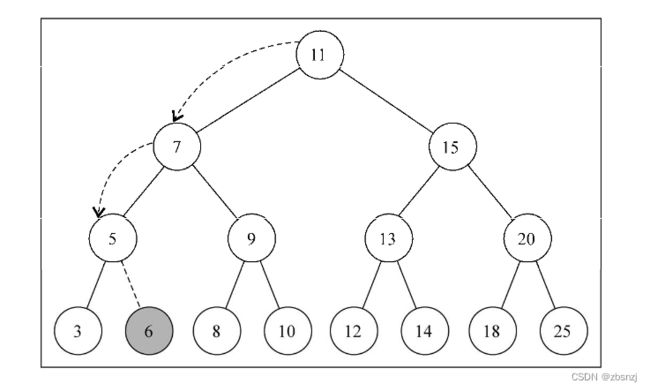
同时我们想要插入一个值为6的键,执行下面的代码:
tree.insert(6);
下面的步骤将会被执行。
(1) 树不是空的,行{3}的代码将会执行。insertNode方法将会被调用(root, key[6])。
(2) 算法将会检测行{4}(key[6] < root[11]为真),并继续检测行{5}(node.left[7]不是null),然后将到达行{7}并调用insertNode(node.left[7], key[6])。
(3) 将再次进入insertNode方法内部,但是使用了不同的参数。它会再次检测行{4}(key[6]
(5) 然后,方法调用会依次出栈,代码执行过程结束。
这是插入键6后的结果:
7.4 树的遍历
7.4.1 中序遍历
中序遍历是一种以上行顺序访问BST所有节点的遍历方式,也就是以从最小到最大的顺序访
问所有节点。
var inOrderTraverseNode = function(node){
if(node !== null){
inOrderTraverseNode(node.left)
console.log(node.key)
inOrderTraverseNode(node.right)
}
}
this.inOrderTraverse = function(){
inOrderTraverseNode(root)
}7.4.2 先序遍历
先序遍历是以优先于后代节点的顺序访问每个节点的。先序遍历的一种应用是打印一个结构
化的文档。
this.preOrderTraverse = function(){
preOrderTraverseNode(root)
}
var preOrderTraverseNode = function(node){
if(node!== null){
console.log(node.key)
preOrderTraverseNode(node.left)
preOrderTraverseNode(node.right)
}
}先序遍历和中序遍历的不同点是,先序遍历会先访问节点本身,然后再访问它的左侧子节点,最后是右侧子节点
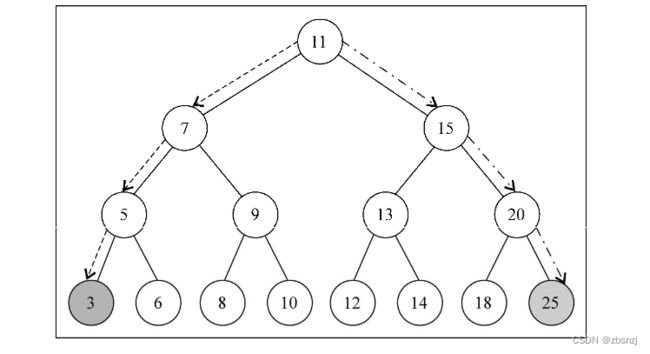
下面是控制台上的输出结果(每个数字将会输出在不同的行):
11 7 5 3 6 9 8 10 15 13 12 14 20 18 25
下面的图描绘了preOrderTraverse方法的访问路径:
7.4.3 后序遍历
后序遍历则是先访问节点的后代节点,再访问节点本身。后序遍历的一种应用是计算一个目
录和它的子目录中所有文件所占空间的大小。
this.postOrderTraverse = function(){
postOrderTraverseNode(root)
}
var postOrderTraverseNode = function(node){
if(node!== null){
postOrderTraverseNode(node.left)
postOrderTraverseNode(node.right)
console.log(node.key)
}
}这个例子中,后序遍历会先访问左侧子节点,然后是右侧子节点,最后是父节点本身。
你会发现,中序、先序和后序遍历的实现方式是很相似的,唯一不同的是fn()的执行顺序。
下面是控制台的输出结果(每个数字将会输出在不同行):
3 6 5 8 10 9 7 12 14 13 18 25 20 15 11
下面的图描绘了postOrderTraverse方法的访问路径:
7.5 搜索树中的值
7.5.1 搜索最小值和最大值
只用眼睛看这张图,你能一下找到树中的最小值和最大值吗?
如果你看一眼树最后一层最左侧的节点,会发现它的值为3,这是这棵树中最小的键。如果
你再看一眼树最右端的节点(同样是树的最后一层),会发现它的值为25,这是这棵树中最大的
键。这条信息在我们实现搜索树节点的最小值和最大值的方法时能给予我们很大的帮助。
this.min = function(){
return minNode(root)
}
var minNode = function(node){
if(node){
while(node && node.left !==null){
node = node.left
}
return node.key
}
return null
}
this.max = function(){
return maxNode(root)
}
var maxNode = function(node){
if(node){
while(node && node.right !==null){
node = node.right
}
return node.key
}
return null
}7.5.2 搜索特定的值
this.search = function(key){
return searchNode(root,key)
}
var searchNode = function(node,key){
if(node === null) return false
if(keynode.key){
return searchNode(node.right,key)
}else {
return true
}
} 在开始算法之前,先要验证作为参数传入的node是否合法(不是null)。如果是null的话,
说明要找的键没有找到,返回false。
如果传入的节点不是null,需要继续验证。如果要找的键比当前的节点小,那么继续在左侧的子树上搜索。如果要找的键比当前的节点大,那么就从右侧子节点开始继续搜索,否则就说明要找的键和当前节点的键相等,就返回true来表示找到了这个键。
可以通过下面的代码来测试这个方法:
7.5.3 移除一个节点
this.remove = function(key){
root = this.removeNode(root,key)
}
var removeNode = function(node,key){
if(node === null) return null // {2}
if(key node.key){ // {6}
node.right = removeNode(node.right,key) // {7}
return node // {8}
}else{
// 第一种情况——一个叶子节点
if(node.left === null && node.right===null){ // {9}
node=null // {10}
return node // {11}
}
// 第二种情况——一个只有一个子节点的节点
if(node.left === null){ // {12}
node=node.right // {13}
return node // {14}
}else if(node.right === null){ // {15}
node=node.left // {16}
return node // {17}
}
// 第三种情况——一个有两个子节点的节点
var aux = findMinNode(node.right) // {18}
node.key = aux.key // {19}
node.right = removeNode(node.rigth,aux.key) // {20}
return node // {21}
}
}
var findMinNode = function(node){
while (node && node.left!==null){
node = node.left
}
return node
} 1、移除一个叶节点
第一种情况是该节点是一个没有左侧或右侧子节点的叶节点——行{9}。在这种情况下,我们要做的就是给这个节点赋予null值来移除它(行{9})。但是当学习了链表的实现之后,我们知道仅仅赋一个null值是不够的,还需要处理指针。在这里,这个节点没有任何子节点,但是它有一个父节点,需要通过返回null来将对应的父节点指针赋予null值(行{11})。
现在节点的值已经是null了,父节点指向它的指针也会接收到这个值,这也是我们要在函数中返回节点的值的原因。父节点总是会接收到函数的返回值。另一种可行的办法是将父节点和节点本身都作为参数传入方法内部。
如果回头来看方法的第一行代码,会发现我们在行{4}和行{7}更新了节点左右指针的值,同样也在行{5}和行{8}返回了更新后的节点。
下图展现了移除一个叶节点的过程:
2. 移除有一个左侧或右侧子节点的节点
现在我们来看第二种情况,移除有一个左侧子节点或右侧子节点的节点。这种情况下,需要
跳过这个节点,直接将父节点指向它的指针指向子节点。
如果这个节点没有左侧子节点(行{12}),也就是说它有一个右侧子节点。因此我们把对它
的引用改为对它右侧子节点的引用(行{13})并返回更新后的节点(行{14})。如果这个节点没
有右侧子节点,也是一样——把对它的引用改为对它左侧子节点的引用(行{16})并返回更新
后的值(行{17})。
下图展现了移除只有一个左侧子节点或右侧子节点的节点的过程:
3. 移除有两个子节点的节点
现在是第三种情况,也是最复杂的情况,那就是要移除的节点有两个子节点——左侧子节点
和右侧子节点。要移除有两个子节点的节点,需要执行四个步骤。
(1) 当找到了需要移除的节点后,需要找到它右边子树中最小的节点(它的继承者——行{18})。
(2) 然后,用它右侧子树中最小节点的键去更新这个节点的值(行{19})。通过这一步,我们改变了这个节点的键,也就是说它被移除了。
(3) 但是,这样在树中就有两个拥有相同键的节点了,这是不行的。要继续把右侧子树中的最小节点移除,毕竟它已经被移至要移除的节点的位置了(行{20})。
(4) 最后,向它的父节点返回更新后节点的引用(行{21})。findMinNode方法的实现和min方法的实现方式是一样的。唯一不同之处在于,在min方法中只返回键,而在findMinNode中返回了节点。
下图展现了移除有两个子节点的节点的过程:
7.6 自平衡树
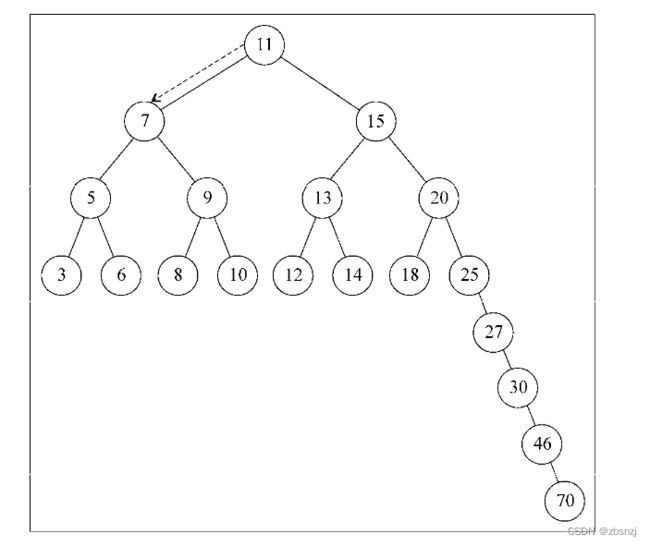
BST存在一个问题:取决于你添加的节点数,树的一条边可能会非常深;也就是说,树的一
条分支会有很多层,而其他的分支却只有几层,如下图所示:
这会在需要在某条边上添加、移除和搜索某个节点时引起一些性能问题。为了解决这个问题,有一种树叫作Adelson-Velskii-Landi树(AVL树)。AVL树是一种自平衡二叉搜索树,意思是任何一个节点左右两侧子树的高度之差最多为1。也就是说这种树会在添加或移除节点时尽量试着成为一棵完全树。
7.6.1 AVL树
AVL树是一种自平衡树。添加或移除节点时,AVL树会尝试自平衡。任意一个节点(不论深
度)的左子树和右子树高度最多相差1。添加或移除节点时,AVL树会尽可能尝试转换为完全树。
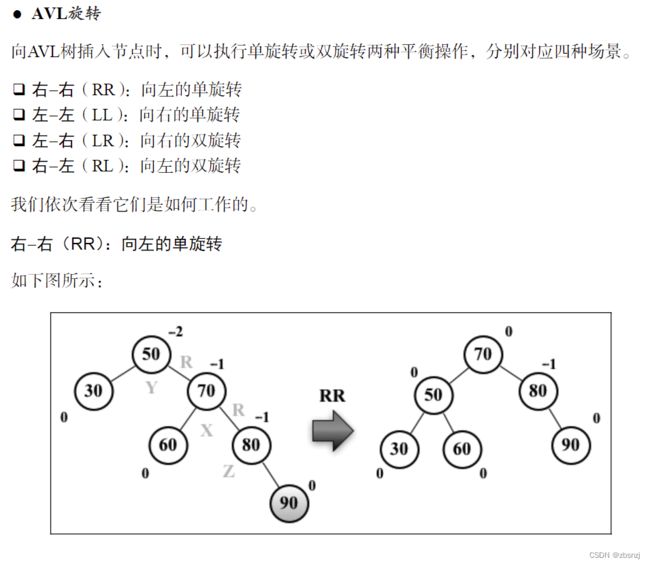
1. 在AVL树中插入节点
在AVL树中插入或移除节点和BST完全相同。然而,AVL树的不同之处在于我们需要检验它
的平衡因子,如果有需要,则将其逻辑应用于树的自平衡。
var insertNode = function(node, element) {
if (node === null) {
node = new Node(element);
} else if (element < node.key) {
node.left = insertNode(node.left, element);
if (node.left !== null) {
// 确认是否需要平衡 {1}
}
} else if (element > node.key) {
node.right = insertNode(node.right, element);
if (node.right !== null) {
// 确认是否需要平衡 {2}
}
}
return node;
}然而,插入新节点时,还要检查是否需要平衡树(行{1}和行{2})。
计算平衡因子
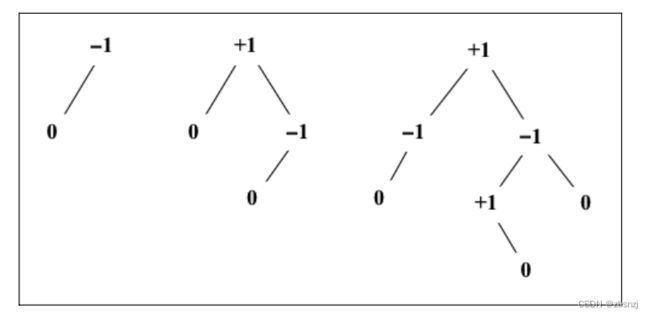
在AVL树中,需要对每个节点计算右子树高度(hr)和左子树高度(hl)的差值,该值(hr-hl)应为0、1或1。如果结果不是这三个值之一,则需要平衡该AVL树。这就是平衡因子
的概念。
下图举例说明了一些树的平衡因子(所有的树都是平衡的):
计算节点高度的代码如下:
var heightNode = function(node){
if(node===null) {
return -1
}else {
return Math.max(heightNode(node.left),heightNode(node.right))+1
}
}因此,向左子树插入新节点时,需要计算其高度;如果高度大于1(即不为1、0和1之一),
就需要平衡左子树。代码如下:
// 替换insertNode方法的行{1}
if ((heightNode(node.left) - heightNode(node.right)) > 1) {
// 旋转 {3}
}
向右子树插入新节点时,应用同样的逻辑,代码如下:
// 替换insertNode方法的行{2}
if ((heightNode(node.right) - heightNode(node.left)) > 1) {
// 旋转 {4}
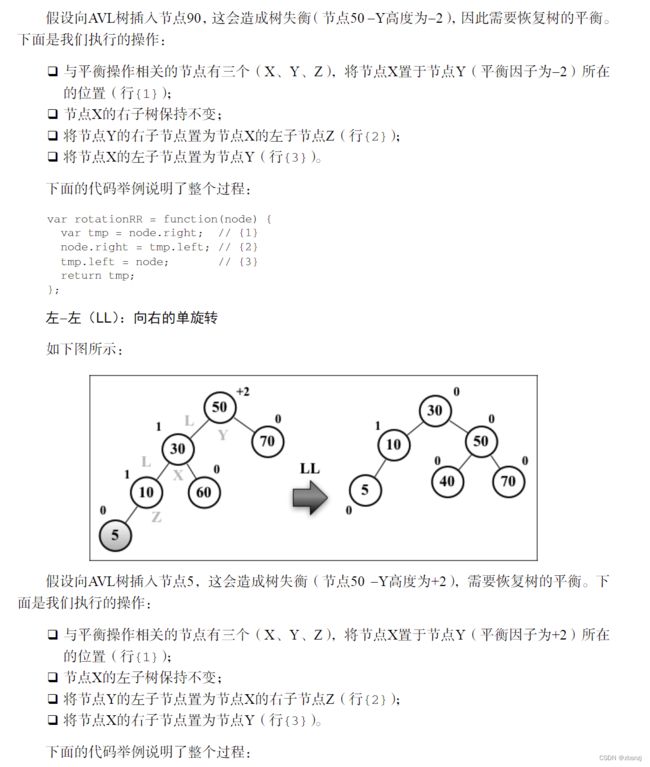
} var rotationLL = function(node) {
var tmp = node.left; // {1}
node.left = tmp.right; // {2}
tmp.right = node; // {3}
return tmp;
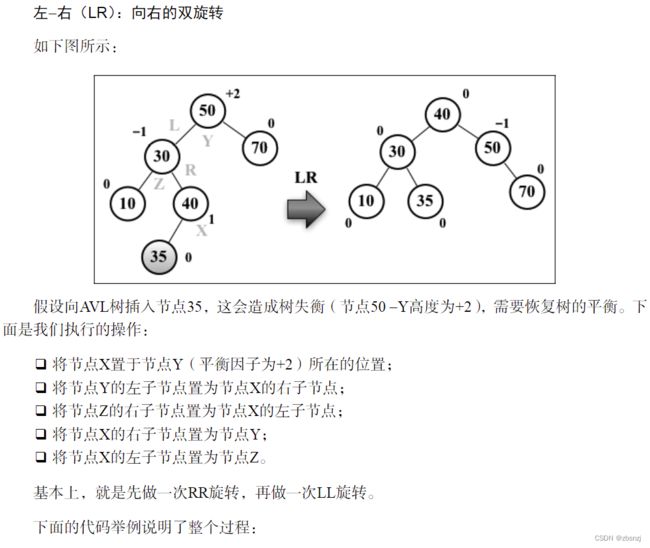
}右-左(RL):向左的双旋转
var rotationRL = function(node) {
node.right = rotationLL(node.right);
return rotationRR(node);
}2. 完成insertNode方法
向左子树插入新节点,且节点的值小于其左子节点时,应进行LL旋转。否则,进行LR旋转。
该过程的代码如下:
// 替换insertNode方法的行{1}
if ((heightNode(node.left) - heightNode(node.right)) > 1){
// 旋转 {3}
if (element < node.left.key){
node = rotationLL(node);
} else {
node = rotationLR(node);
}
} 向右子树插入新节点,且节点的值大于其右子节点时,应进行RR旋转。否则,进行RL旋转。
该过程的代码如下:
// 替换insertNode方法的行{2}
if ((heightNode(node.right) - heightNode(node.left)) > 1){
// 旋转 {4}
if (element > node.right.key){
node = rotationRR(node);
} else {
node = rotationRL(node);
}
}7.7 小结
function BinarySearchTree(){
var Node = function(key){ // {1}
this.key = key
this.left = null
this.right = null
}
var root = null // {2}
var insertNode = function(node,newNode){
if(newNode.keynode.key){
return searchNode(node.right,key)
}else {
return true
}
}
this.remove = function(key){
root = this.removeNode(root,key)
}
var removeNode = function(node,key){
if(node === null) return null // {2}
if(key node.key){ // {6}
node.right = removeNode(node.right,key) // {7}
return node // {8}
}else{
// 第一种情况——一个叶子节点
if(node.left === null && node.right===null){ // {9}
node=null // {10}
return node // {11}
}
// 第二种情况——一个只有一个子节点的节点
if(node.left === null){ // {12}
node=node.right // {13}
return node // {14}
}else if(node.right === null){ // {15}
node=node.left // {16}
return node // {17}
}
// 第三种情况——一个有两个子节点的节点
var aux = findMinNode(node.right) // {18}
node.key = aux.key // {19}
node.right = removeNode(node.rigth,aux.key) // {20}
return node // {21}
}
}
var findMinNode = function(node){
while (node && node.left!==null){
node = node.left
}
return node
}
var insertNode = function(node, element) {
if (node === null) {
node = new Node(element);
} else if (element < node.key) {
node.left = insertNode(node.left, element);
if (node.left !== null) {
// 确认是否需要平衡 {1}
if(heightNode(node.left)-heightNode(node.right)>1){
// 旋转{3}
}
}
} else if (element > node.key) {
node.right = insertNode(node.right, element);
if (node.right !== null) {
// 确认是否需要平衡 {2}
if(heightNode(node.right)-heightNode(node.left)>1){
// 旋转{4}
}
}
}
return node;
}
var heightNode = function(node){
if(node===null) {
return -1
}else {
return Math.max(heightNode(node.left),heightNode(node.right))+1
}
}
var rotationRR = function(node) {
var tmp = node.right; // {1}
node.right = tmp.left; // {2}
tmp.left = node; // {3}
return tmp;
}
var rotationLL = function(node) {
var tmp = node.left; // {1}
node.left = tmp.right; // {2}
tmp.right = node; // {3}
return tmp;
}
var rotationLR = function(node) {
node.left = rotationRR(node.left);
return rotationLL(node);
}
var rotationRL = function(node) {
node.right = rotationLL(node.right);
return rotationRR(node);
}
}
var tree = new BinarySearchTree();
tree.insert(11);
tree.insert(7);
tree.insert(15);
tree.insert(5);
tree.insert(3);
tree.insert(9);
tree.insert(8);
tree.insert(10);
tree.insert(13);
tree.insert(12);
tree.insert(14);
tree.insert(20);
tree.insert(18);
tree.insert(25);
tree.insert(6);
console.log(tree.search(1)? 'key 1 found':'key 1 not found')
console.log(tree.search(8)? 'key 8 found':'key 8 not found')