用 MATLAB 实现的计算机CT断层扫描图像重建项目源码
完整源码资源下载链接
计算机断层扫描图像重建
介绍
计算机断层扫描是堆叠在一起的 X 射线图像的集合,以获得作为诊断图像第三维的深度信息。这些“堆叠的” X 射线图像作为正弦图从 CT 机架接收,代表对象单层的 X 射线吸收剖面。该项目的目标是重建该单层的原始 2D 图像,并使用光衰减信息区分受试者组织的不同 X 射线吸收水平。
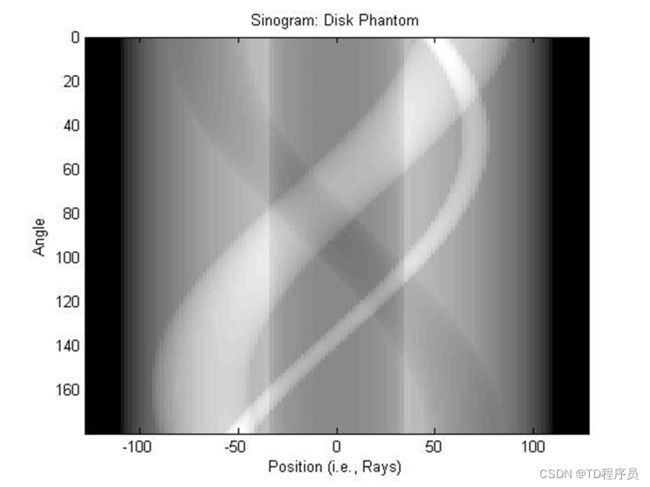
下面我们看到一个示例,说明如何通过 X 射线束穿过身体(左)的横截面层来形成正弦图(右),每个角度的 X 射线吸收都会生成衰减曲线图。
项目详情
对象在 CT 机架旋转的每个角度处的 X 射线投影都会生成正弦图,其中 Y 轴显示以度为单位的角度,而 X 轴显示空间距离。
我创建了一个示例正弦图,该项目的目标是构造其相应的幻像对象。我们将确定通过体模内不同层的 X 射线衰减,从而获得物体的物体密度分布。
| 输入正弦图 |
输出应该接近 |
| 编辑 |
第零时刻
如上图所示,第 0 时刻是 X 射线首次以每个角度照射 CT 探测器时的响应。这将是每个角度(X 轴)处的衰减幅度(Y 轴)的总和,因此将是正弦图 256 个角度投影列中每一个的总和。
它是一条平坦的线的显着结果是因为无论从哪个角度进行投影,由于物体特征是静态的,衰减强度的总和将是恒定的。
简单的背投影图像
简单的反投影是通过将投影叠加在一起来计算的,这为图像的所有组件创建了浓度梯度。单列将包含单个角度投影的衰减信息。总共有 256 个角度投影,对应于正弦图上显示的 180 度。
因此,我们一次选择一列,将衰减幅度信息涂抹在 128 行上,然后将其旋转到与以度为单位对应的角度(第 256 个投影对应于 180 度,因此第 n 个投影将对应于 n*180/256 度) 。
与真实输出图像还不够接近,但肯定更近了一步! 每次将新的投影涂抹添加到旧的投影涂抹时,都会一次又一次地添加特定的“灰度”。这使得在背投图像上暗点显示相对较暗,而亮点则显示相对较亮。
拉姆拉克过滤器
为了执行正弦图的滤波反投影,我们需要构建将在频域中使用的滤波器。这将帮助我们轻松地将其乘以傅里叶变换的正弦图,而不是执行卷积。然后将滤波器响应与傅立叶变换(和移位)正弦图相乘。结果是频域中的 Ram-Lak(高通滤波器)滤波正弦图,且所有零频率均居中。
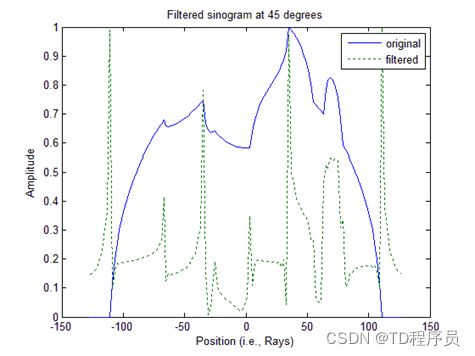
为了获得原始频率分布,我们先进行逆傅里叶位移,然后对其进行逆傅里叶变换,以获得空间域正弦图。我们看到滤波器响应如何比未滤波的对手更具选择性,并且我们可以看到当检测到边缘时存在幅度尖峰。
| 过滤正弦图 |
过滤后与原始 |
与我们简单的背投影图像相比,我们看到 Ram-Lak 滤波器能够去除低频噪声(雾霾),提高对比度,从而提高总信噪比。分辨率似乎也有所提高,但主要是由于清晰度的提高和对比度的提高。
与汉明比较
我们还可以探索 MATLAB 的内置函数来执行此操作。为此,我们使用 Radon 和逆 Radon 变换。
theta=0:180;
[R,rad_angles]=radon(phantom,theta); % as shown in radon help file
imagesc(rad_angles,theta,R'); colormap('gray');
title('Sinogram Generated Using radon Function')
xlabel('Position')
ylabel('Angle')
RamLak_filtered=iradon(R, theta, 'linear','Ram-Lak', 1.0, size(phantom,1));
imagesc(RamLak_filtered); colormap('gray');
title('Filtered Backprojection Using iradon Function and Ram-Lak Filter')
xlabel('Position')
ylabel('Position')
Hamming_filtered=iradon(R, theta, 'linear','Hamming', 1.0, size(phantom,1));
imagesc(Hamming_filtered); colormap('gray');
title('Filtered Backprojection Using iradon Function and Hamming Filter')
xlabel('Position')
ylabel('Position')
| Ram-Lak 滤波输出 |
汉明滤波输出 |
Ram-Lak 滤波器是高通滤波器,与中频通 Hamming 滤波器相比,我们看到 Ram-Lak 滤波后的图像比 Hamming 滤波后的图像具有更清晰的特征。因此,为了使医学图像具有更好的清晰度和分辨率,Ram-Lak 滤波器会更适合。