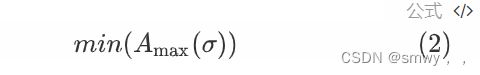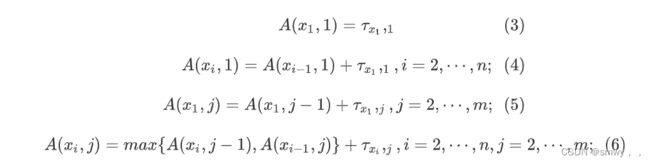基于模拟退火算法的置换流水车间调度问题的探论
基于模拟退火算法的置换流水车间调度问题的探论
摘 要：流水车间调度问题是求解n个工件经过m台机器加工的工件加工顺序，从而最小化完工时间的问题，需要满足每台机器同时只能加工一个工件。置换流水车间调度问题实际上是流水车间调度问题的一种特殊情况，即默认所有机器上的加工顺序都是一样的。笔者将使用模拟退火算法（Simulated Annealing, SA)求解。模拟退火算法来源于固体退火原理，是一种基于概率的算法，其出发点是基于物理中固体物质的退火过程和一般组合优化问题之间的相似性。它从某一较高初温出发，伴随温度参数的不断下降，接纳比当前解较差的邻域解的概率下降，但总体上能在局部最优解时能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法，理论上算法具有概率的全局优化性能，因此适用于解决置换流水车间调度问题，较容易地跳出局部最优解从而达到比较趋近于全局最优解的水平。本实验对初始温度、迭代次数、退火率进行了多组测试，得到了大量真实的实验结果，得到了一系列可靠的结论。
关键词：模拟退火算法；置换流水车间调度问题；PFSP
1.引言
1.1背景介绍
生产调度是在某些生产条件约束下，合理确定每个加工对象的加工路径、加工时间和操作等，以实 现某些生产目标，可以定义为“把有限的资源在时间 上分配给若干任务，以满足一个或多个目标”1。而置换流水车间调度问题(permutation flow-shop scheduling problem, PFSP)就是生产调度问题的一个具象化，置换流水车间调度问题旨在最小化完成加工总时间。即使置换流水车间调度问题形式上比较简单，但3台机器以上的置换流水车间调度问题已被证明属于NP-hard问题。同时精确算法和启发式算法在求解大规模调度问题上仍存在一定局限性，因此为了在合理时间内得到问题的最优解，智能优化算法应运而生，其中模拟退火算法便是性能优秀的算法之一。
1.2置换流水车间调度问题详细介绍
流水车间调度问题研究n个工件经过m台机器加工的过程，同时限制每个工件只能在各台机器上加工一次，每台机器一次只能加工一个工件，各工件在每台机器上的加工时间已知。目的是求得工件加工顺序，从而最小化完工时间。置换流水车间调度问题实际上在流水车间调度问题的基础上增加了一个约束条件，即默认所有机器上的加工顺序都是一样的。用数学语言可将置换流水车间问题描述如下：
假设表示工件i在机器j上的加工时间；假设=(,,,,)为工件的一种加工顺序；假设为工件在机器j上完成加工的时间。
由上，最大完工时间为：
目标函数：
约束条件：
公式(1)表示最大完工时间为最后一个工件经过最后一台机器加工的完成时间。公式(2)表示目标为最小化最大完工时间，与之对应的调度排序方案即为目标为最小化最大完成时间的PFSP问题的最优调度方案2。公式(3)表示第一个工件在机器1上的完工时间，即第一个工件在机器1上的加工时间。公式(4)表示第i个工件在机器1上的完工时间，即第i-1个工件在第一台机器上的完工时间加上第i个工件在机器1上的加工时间。公式(5)表示第1个工件在机器j上的完工时间，即第1个工件在机器j-1上的完工时间加上工件在机器j上的加工时间。公式(6)表示工件在机器j上的完工时间要取工件在机器j上的完工时间和工件在机器j-1上的完工时间的较长时间以及工件在机器j上的加工时间之和，从而保证一台机器同时只加工一个工件，一个工件同时也只在一台机器上加工。
1.3解决方案概述
考虑到登山算法容易陷入局部最优解和初值依赖的问题，本文采用模拟退火算法，该算法通过概率接收较差邻域解来避免陷入局部最优解。模拟退火算法的步进规则是随机交换某两个零件的加工顺序，在计算目标函数时模拟时间的进行。首先随机选择一种工件的加工顺序，然后经过处理得到最大完工时间，由随机交换某两个工件的加工顺序得到邻域解，从而概率地跳出，最终趋近于最优解。实验结果显示通过对不同用例适当调整温度以及其他参数可以提高效率。
本文后续部分组织如下。第2节详细陈述使用的方法，第3节报告实验结果，第4节对讨论本文的方法并总结全文。
2.算法设计
2.1模拟退火算法思路简介
模拟退火算法（Simulated Annealing, SA)来源于固体退火原理，是一种基于概率的算法，其出发点是基于物理中固体物质的退火过程和一般组合优化问题之间的相似性。 它从某一较高初温出发，伴随温度参数的不断下降，接纳比当前解较差的邻域解的概率下降，但总体上能在局部最优解时能概率性地跳出并最终趋于全局最优，是一种通用的优化算法，理论上算法具有概率的全局优化性能，因此适用于解决置换流水车间调度问题，较容易地跳出局部最优解从而达到比较趋近于全局最优解的水平。在这个问题中的步进规则是随机交换某两个零件的加工顺序，在计算目标函数时模拟时间的进行，首先随机选择一种工件的加工顺序，然后经过处理得到最大完工时间，由随机交换某两个工件的加工顺序得到邻域解，从而概率地跳出，最终趋近于最优解。在徐徐冷却的过程中，若连续不接纳邻域解的次数超过50次，或最近100次的解的质量的平均值几乎不再上升，则结束。
2.2模拟退火算法详细介绍
2.2.1模拟退火算法
2.2.2Metropolis算法
2.2.3目标函数与步进规则
2.2.4初始状态
初始状态即起点的选择对于模拟退火算法来说至关重要，如果模拟退火算法选择了一个较为合适的初始状态会大大提高算法的优化结果并减少优化时间。将某次得到的优化结果作为初始状态也是进一步优化结果的途径之一。本文选择随机生成一个加工工件顺序。
2.2.5伪代码
Input:一个用例的工件矩阵instance,一系列参数
Variables:当前调度顺序current_schedule，当前解目标函数值current_time，冷却因子theta,目标函数连续重复次数count1，连续未接收新解计数器count2，未接受新解次数上限Max_Maintain，目标函数值未变化上限Max_Unchanged
for epoch from 1 to 10 do
Initialize:init_schedule←随机生成初始解
for t←1 to ∞ do
T←T*theta
next_schedule←current_schedule的步进
ΔE = current_time - next_time(next_schedule)
if ΔE>0 then
current_schedule←next_schedule,current_time = next_time且重置两个计数器
else
生成0到1间随机浮点数po
if po< $e^{\frac{t-new\_t}{T} }$ then
accept new schedule and update two counts
else
update two counts
if count1>Max_Unchanged ||count2 >Max_Maintain then break
Output:一个用例的最小最大总加工时间与其对应的工件顺序
2.2.6算法核心部分的复杂度分析
3.实验
3.1实验设置
3.2实验结果
3.2.1实验客观结果
表1 实验结果
| instance | 调度方案 | 加工工时 |
|---|---|---|
| 0 | [7, 2, 0, 6, 8, 4, 10, 1, 5, 3, 9] | 7038 |
| 1 | [3, 1, 0, 4, 2] | 6269 |
| 2 | [5, 2, 3, 6, 9, 1, 0, 7, 4, 8] | 5977 |
| 3 | [8, 4, 9, 3, 7, 2, 0, 10, 11, 6, 5, 1] | 7332 |
| 4 | [2, 12, 5, 4, 11, 7, 9, 8, 14, 13, 10, 0, 6, 1, 3] | 9231 |
| 5 | [3, 1, 0, 2, 6, 4, 8, 7, 5] | 7498 |
| 6 | [15, 1, 13, 12, 9, 3, 8, 0, 11, 10, 18, 14, 7, 2, 4, 17, 16, 6, 5] | 1396 |
| 7 | [4, 13, 3, 17, 11, 14, 7, 9, 15, 6, 1, 10, 8, 18, 12, 16, 0, 2, 5] | 1932 |
| 8 | [11, 5, 8, 1, 0, 14, 3, 16, 4, 13, 7, 2, 12, 10, 6, 9, 15, 17] | 1012 |
| 9 | [14, 12, 17, 18, 7, 8, 1, 16, 10, 2, 3, 11, 6, 15, 5, 13, 9, 0, 4] | 1920 |
| 10 | [7, 8, 34, 33, 36, 38, 30, 39, 3, 11, 20, 2, 14, 31, 13, 23, 5, 35, 29, 21, 32, 9, 12, 19, 0, 16, 28, 27, 24, 26, 15, 4, 17, 37, 22, 6, 18, 1, 10, 25] | 2769 |
由于初始状态的生成具有随机性且算法的概率性趋近全局最优解，在一般情况下运行程序得到的结果可能和最优解偏差0~0.3%。
3.2.2实验结果分析
由于初始状态的生成具有随机性且算法的概率性趋近全局最优解，在一般情况下运行程序得到的结果可能和最优解偏差0~0.3%。
3.2.3参数对比实验
-
初始温度对照（100 10000 1000000 100000000 10000000000）
表2 初始温度对比实验结果
对照 100 10000 1000000 100000000 10000000000 1 7038 7038 7038 7038 7038 2 6269 6269 6269 6269 6269 3 5977 5977 5977 5977 5977 4 7332 7332 7332 7332 7332 5 9231 9231 9231 9231 9231 6 7498 7498 7498 7498 7498 7 1399 1396 1412 1402 1394 8 1970 1932 1917 1927 1924 9 1012 1012 1012 1012 1012 10 1892 1920 1929 1929 1919 11 2766 2769 2777 2766 2773 由初始温度对比实验易知：高温对于结果的改善有限，模拟退火算法对于温度并不敏感，但是高温可以增加初期探索区间，有利于改善结果表现。
-
冷却因子theta对照（0.9 0.95 0.99 0.999 0.9999）
表3 冷却因子theta对比实验结果
对照 0.9 0.95 0.99 0.999 0.9999 1 7038 7038 7038 7038 7038 2 6332 6269 6332 6269 6269 3 5977 5977 5977 5977 5977 4 7332 7332 7332 7332 7332 5 9231 9231 9231 9231 9231 6 7498 7498 7498 7498 7498 7 1423 1412 1401 1427 1421 8 1925 1992 1970 1942 1949 9 1067 1012 1010 1012 1012 10 2016 1994 1980 1931 1920 11 2880 2806 2901 2836 2769 由冷却因子对比实验易知：冷却因子和初始温度决定了前期的温度，如果冷却因子高或者初始温度高，会保持更长时间的高温，有利于跳出局部最优。
4.总结
本文采用了模拟退火算法的方式对置换流水车间调度问题的一些示例进行了最优解的寻找，后续本文对其中的参数进行了对比试验得到了一系列结果，进一步熟悉了模拟退火算法的思想。
本文的缺点在于没有采用合适的启发式搜索而仅仅采用了随即邻域搜索，同时本文进行的参数改动仍然较少，未能对每一个用例找到一个兼顾时间和效率的最合适的参数。
参考文献：
[ 1 ]: 黎阳，李新宇，牟健慧.基于改进模拟退火算法的大规模置换流水车间调度 [J].计算机集成制造系统，2020，26(2): 355-375.
[2] 于承敏,郑丽萍,张民.粒子群算法解决置换流水车间调度问题方法综述J.机械设计与制造,2012(08):84-86.DOI:10.19356/j.cnki.1001-3997.2012.08.031.
[ 3 ]:庞峰. 模拟退火算法的原理及算法在优化问题上的应用[D].吉林大学,2006.
附录A：考虑无等待约束的改进算法
A.0无等待约束的含义
无等待约束指的是工件在车间内被加工的过程中不需要等待前一道工序的完成，即一旦工件完成当前加工立即进入下一机器进行加工。无等待约束在生活中常用在钢铁加工与食物产品等行业。
A.1算法改进
原始算法通过模拟时间的推进来计算加工完成时间，而此处需要进行以下改进：
-
使用二维数组completionTime来记录每个工件在每个机器上的加工完成时间，以便后续计算加工完成时间。
-
当工件每次进入下一个机器，更新completionTime数组中该工件在当前机器上的加工完成时间，同时更新总加工完成时间。