Java递归算法
在程序设计中,递归的设计就是利用了栈的“后进先出”的思想。利用栈可以将递归程序转换为非递归程序。
3.3.1 递 归
递归是指在函数的定义中,在定义自己的同时又出现了对自身的调用。如果一个函数在函数体中直接调用自己,就称为直接递归函数。如果经过一系列的中间调用,间接调用自己的函数就称为间接递归调用。
1. 递归函数
例如,n的阶乘递归定义如下:
n的阶乘算法如下:
public static long fact(int n)
//n的阶乘的非递归算法实现
{
long f = 1;
int i;
for(i=1;i
return f;
}
Ackerman函数定义如下:
Ackerman函数相应算法如下:
public static long Ack(long m,long n)
//Ackerman递归算法实现
{
if(m == 0)
return n + 1;
else if(n==0)
return Ack(m - 1, 1);
else
return Ack(m - 1, Ack(m, n - 1));
}
2. 递归调用过程
递归问题可以分解成规模小且性质相同的问题加以解决。下面我们以著名的汉诺塔问题为例来说明递归的调用过程。
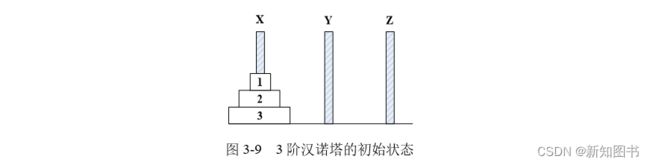
n阶汉诺塔问题。假设有3个塔座X、Y、Z,在塔座X上放置n个直径大小各不相同、从小到大编号为1,2,…,n的圆盘,如图3-9所示。要求将X轴上的n个圆盘移动到塔座Z上并要求按照同样的叠放顺序排列,圆盘移动时必须遵循以下规则:
(1)每次只能移动一个圆盘。
(2)圆盘可以放置在X、Y和Z中的任何一个塔座。
(3)任何时候都不能将一个较大的圆盘放在较小的圆盘上。
图3-9 3阶汉诺塔的初始状态
如何实现将放在X上的圆盘按照规则移动到Z上呢?当n=1时,问题比较简单,直接将编号为1的圆盘从塔座X移动到Z上即可。当n>1时,需要利用塔座Y作为辅助塔座,若能将放置在编号为n上的n-1个圆盘从塔座X上移动到Y上,则可以先将编号为n的圆盘从塔座X移动到Z上,然后将塔座Y上的n-1个圆盘移动到塔座Z上。而如何将n-1个圆盘从一个塔座移动到另一个塔座又成为与原问题类似的问题,只是规模减小了1,因此可以用同样的方法解决。这是一个递归问题,汉诺塔的算法描述如下:
public static void Hanoi(int n,String A,String B,String C)
//将塔座A上从小到大自上而下编号为1到n的圆盘按照规则搬到塔座C上,B可以作为辅助塔座
{
if(n == 1)
move(1, A, C); //将编号为1的圆盘从A移动到C
else {
Hanoi(n - 1, A, C, B); //将编号为1到n-1的圆盘从A移动到B,C作为辅助塔座
move(n, A, C); //将编号为n的圆盘从A移动到C
Hanoi(n - 1, B, A, C); //将编号为1到n-1的圆盘从B移动到C,A作为辅助塔座
}
}
public static void move (int n, String tempA, String tempB) {
System.out.println("move plate"+n+" from column "+tempA+" to column "+ tempB);
}
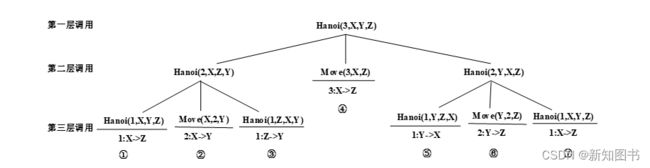
下面以n=3为例,来说明汉诺塔的递归调用过程,如图3-10所示。当n>1时,需要3个过程移动圆盘。
第1个过程,将编号为1和2的圆盘从塔座X移动到塔座Y。
第2个过程,将编号为3的圆盘从塔座X移动到塔座Z。
第3个过程,将编号为1和2的圆盘从塔座Y移动到塔座Z。
图3-10 汉诺塔的递归调用过程
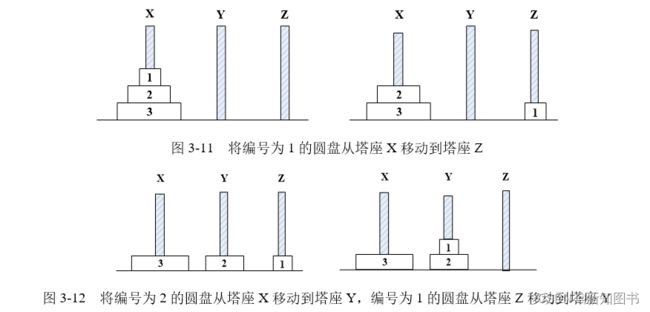
第1个过程,通过调用Hanoi(2,X,Z,Y)来实现。Hanoi(2,X,Z,Y)又调用自己,完成将编号为1的圆盘从塔座X移动到塔座Z,如图3-11所示。编号为2的圆盘从塔座X移动到塔座Y,编号为1的圆盘从塔座Z移动到塔座Y,如图3-12所示。
第2个过程完成将编号为3的圆盘从塔座X移动到塔座Z,如图3-13所示。
第3个过程通过调用Hanoi(2,Y,X,Z)来实现圆盘移动。通过再次递归完成将编号为1的圆盘从塔座Y移动到塔座X,如图3-14所示。将编号为2的圆盘从塔座Y移动到塔座Z,将编号为1的圆盘从塔座X移动到塔座Z,如图3-15所示。
本问节选自《图解Java数据结构与算法(微课视频版)》。