LeetCode刷题--- 子集

 个人主页：元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客

个人专栏

• 力扣递归算法题【  http://t.csdnimg.cn/yUl2I   】
• 【C++】          【  http://t.csdnimg.cn/6AbpV 】
• 数据结构与算法【  http://t.csdnimg.cn/hKh2l  】

---

前言：这个专栏主要讲述递归递归、搜索与回溯算法，所以下面题目主要也是这些算法做的  

我讲述题目会把讲解部分分为3个部分：
1、题目解析

2、算法原理思路讲解

3、代码实现

---

子集

题目链接：子集

题目

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10
• nums 中的所有元素 互不相同

---

解法

题目解析

题目意思很简单，给我们一个数组，返回其 所有可能的子集

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

---

算法原理思路讲解    

解法一

为了获得 nums 数组的所有⼦集，我们需要对数组中的每个元素进⾏选择或不选择的操作，即nums 数组⼀定存在 【2^数组⻓度】 个⼦集。对于查找⼦集，具体可以定义⼀个数组，来记录当前的状态，并对其进⾏递归。对于每个元素有两种选择：1. 不进⾏任何操作；2. 将其添加⾄当前状态的集合。在递归时我们需要保证递归结束时当前的状态与进⾏递归操作前的状态不变，⽽当我们在选择进⾏步骤 2 进⾏递归时，当前状态会发⽣变化，因此我们需要在递归结束时撤回添加操作，即进⾏回溯。

一、画出决策树

​

决策树就是我们后面设计函数的思路

---

 二、设计代码

（1）全局变量

vector> ret;
 vector path;

（2）设计递归函数

void dfs(vector& nums, int pos);

递归流程如下

1. 递归结束条件：如果当前需要处理的元素下标越界，则记录当前状态并直接返回；
2. 在递归过程中，对于每个元素，我们有两种选择：
   1. 不选择当前元素，直接递归到下⼀个元素；
   2. 选择当前元素，将其添加到数组末尾后递归到下⼀个元素，然后在递归结束时撤回添加操作；
3. 所有符合条件的状态都被记录下来，返回即可。

---

解法二 

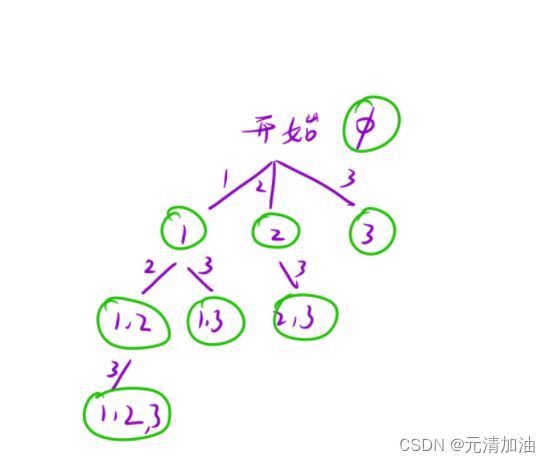
一、画出决策树

决策树就是我们后面设计函数的思路

---

 二、设计代码

（1）全局变量

vector> ret;
 vector path;

1.递归函数头设计

void dfs(vector& nums, int pos);

参数：nums 数组，pos 在数组中的位置 

递归流程如下

1. 在递归过程中，对于每个元素，我们只能向后选择：
   1. 选择当前元素，将其添加到数组末尾后递归到下⼀个元素，然后在递归结束时撤回添加操作（也即是回溯）
2. 所有符合条件的状态都被记录下来，返回即可。

 

---

代码实现

解法一

时间复杂度：O(n×2^n)。一共 2^n个状态，每种状态需要 O(n) 的时间来构造子集。

空间复杂度：O(n)。临时数组 t 的空间代价是 O(n)，递归时栈空间的代价为 O(n)。

class Solution
{
 vector> ret;
 vector path;
public:

    void dfs(vector& nums, int pos)
    {
        if(pos == nums.size())
        {
            ret.push_back(path);
            return;
        }
        // 选
        path.push_back(nums[pos]);
        dfs(nums, pos + 1);
        path.pop_back(); // 恢复现场
        // 不选
        dfs(nums, pos + 1);
    }
    
    vector> subsets(vector& nums) 
    {
        dfs(nums, 0);
        return ret;
    }
    
};

---

解法二

class Solution
{
 vector> ret;
 vector path;
 public:
    vector> subsets(vector& nums) 
    {
    
        dfs(nums, 0);
        return ret;
    }
    void dfs(vector& nums, int pos)
    {
        ret.push_back(path);
        for(int i = pos; i < nums.size(); i++)
        {
            path.push_back(nums[i]);
            dfs(nums, i + 1);
            path.pop_back(); // 恢复现场
        }
    }
};