数学learning

目录

移动平均

简单移动平均

加权移动平均

指数移动平均

矩阵求导

 矩阵对标量求导 Matrix-by-scalar

标量对矩阵求导 Scalar-by-matrix

参考博客

---

移动平均

        优化算法里面会涉及到一个知识点：指数移动平均。

        但是为了知识的完整性，这里会将常见的移动平均全部过一遍

        首先，移动平均法是根据时间序列资料逐渐推移，依次计算包含一定项数的时序平均数，以反映长期趋势的方法。当时间序列的数值由于受到周期变动和不规则变动的影响，起伏较大，不易显示出发展趋势时，可采用移动平均法，消除这些因素的影响，分析、预测序列的长期趋势。由此可以看出移动平均是技术分析中一种分析时间序列的常用工具

        常见的移动平均包括：

• 简单移动平均(SMA)
• 加权移动平均(WMA) --加权平均
• 指数移动平均(EMA) --指数平滑

简单移动平均

        首先举个例子若依次得到测定值 时，按顺序取一定个数所做的全部算术平均值。 这里假设按照三个区算术平均数，则移动平均值为:

        设观测序列为，取移动平均的项数.一次简单移动平均值计算公式为:

        (1)式为简单移动平均值计算的定义式，但是我们发现由(1)式可以推出(2)式，我们可以把(2)式的括号打开，那么(2)式子中前面的累加和中的最大项会变成，最小项会因为相互抵消，重新变为，我们发现就是(1)式，很简单的一个变换。

        当预测目标的基本趋势是在某一水平面上下波动时，可用一次简单移动平均法建立预测模型:

         利用最后N项求完的简单移动平均值作为预测的值。其预测标准误差为:

        一般N的取值范围:5<=N<=200.当历史序列的基本趋势变化不大且序列中随机变动成分较多时，N的取值应较大一些。否则N的取值应小一些，在由确定的季节变动周期资料中，移动平均的项数应取周期长度。选择最佳N值的一个有效方法是，比较若干模型的预测误差。预测误差小的好。

        简单移动平均法只适合做近期预测，而且是预测目标的发展趋势变化不大的情况。 如果目标的发展趋势存在其它的变化，采用简单移动平均法就会产生较大的预测偏差和滞后。 

加权移动平均

        在简单移动平均公式中，每期数据在求平均时的作用是等同的。但是，每期数据所包含的信息量不一样，近期数据包含着更多关于未来情况的信心。因此，把各期数据等同看待是不尽合理的，应考虑各期数据的重要性，对近期数据给予较大的权重，这就 是加权移动平均法的基本思想。 

        总结一句话就是加权移动平均法，是在简单移动平均法的基础上给每一项加上一个权值,公式如下:

        在加权移动平均法中, wtwt 的选择，同样具有一定的经验性。一般的原则是：近期 数据的权数大，远期数据的权数小。至于大到什么程度和小到什么程度，则需要按照预 测者对序列的了解和分析来确定。 

指数移动平均

        一次移动平均实际上认为近 期数据对未来值影响相同，都加权；而 期以前的数据对未来值没有影响，加权为 0。但是，二次及更高次移动平均数的权数却不是 ，且次数越高，权数的结构越复杂，但永远保持对称的权数，即两端项权数小，
        中间项权数大，不符合一般系统的动态性。一般说来历史数据对未来值的影响是随时间间隔的增长而递减的。所以，更切合实际的方法应是对各期观测值依时间顺序进行加权平均作为预测值。指数平滑法可满足这一要求，而且具有简单的递推形式。

        那么究竟什么是指数移动平均，指数移动平均（exponential moving average，EMA或EWMA）是以指数式递减加权的移动平均。各数值的加权影响力随时间而指数式递减，越近期的数据加权影响力越重，但较旧的数据也给予一定的加权值。参考吴恩达深度学习课程中的计算公式进行描述

设时刻的实际数值为, 时刻的EMA为,时刻的EMA为，计算时刻的指数移动平均公式为：

  为权重因子, 通常取值为接近于1的值，如0.9， 0.98， 0.99， 0.999等。越小，过去过去累计值的权重越低，当前抽样值的权重越高，移动平均值的实时性就越强。反之  越大，吸收瞬时突发值的能力变强，平稳性更好

        是如何表示指数移动平均的?

我们这里设

......

逐层会带:

这里实际上是对时刻之前(包括)实际数值的加权平均,实际数值的加权平均,时间离得越远,权重越小,而且是指数式递减的，所以又叫指数加权移动平均 / 指数衰减移动平均

与一般的加权平均相比，使用指数移动平均的好处在于：

• 不需要保存前面所有时刻的实际数值，并且在计算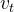的过程中是逐步覆盖的，因此可以减少内存的占用
• 在有些场景下，其实更符合实际情况的，例如股票价格，天气等，上一个时间步对当前时间步影响最大

        但是因为当 EMA 在初始化或者在开始计算的时候，它是有偏的，特别是在序列的开始阶段。这是由于 EMA 的初始值 () 通常被设置为 0 或者被设置为非常小的数，这将导致 EMA 在开始时偏向于较小的值，从而低估了真实的平均值。

        为了减少这种偏差，我们可以应用偏差修正。修正后的 EMA 定义如下：

        在这里，() 是时间步或迭代的次数，() 是偏差校正后的 EMA 值。当 () 很小时，() 接近1，这样做可以显著提高修正后的 EMA 值，使其更接近实际的平均值。随着 () 的增加，() 接近1，这意味着修正越来越小，当 () 足够大以后，EMA 的值就不再需要修正。

下面是最最最重要的问题，权重因子如何确定

权重因子是指数移动平均计算中最关键的参数，如何确定权重因子的大小成为一个关键问题。下面重新推导指数移动平均公式，进一步理解指数移动平均的含义，从而确定权重因子的大小。

设,求解的表达式

        指数移动平均值，本质上前100项数值的加权平均。这时我们考虑，到底需要平均多少项的数值。实际上，在计算当前项的指数移动平均值时，我们会加权平均，包含当前项的之前所有项的值。

        但是我们发现，权重随着指数系数的增加而减小，并趋近于0，例如,所以我们可以假设这一项后面的值后忽略不计，即我们假设存在一个阈值，当项的权重系数大于阈值时为有效项；当权重系数衰减到低于阈值则为无效项

        这里的权重衰减阈值设为自然数的倒数为  ，进一步说，当权重系数小于  时忽略当前项及之后项的加权值。权重因子的作用本质上是控制指数权重平均计算中有效项的数目，即指数平滑有效窗口的大小。

        权重因子可以表示为,带入极限得

        我们关心的并不是权重因子的大小，而是指数移动平滑的步长大小，即权重系数,其中  对应的数值,表示平滑窗口/周期的大小。

        所以我们很容易得得出,怎么理解呢，因为我们设置了权重系数最小为,所以可以理解为所以就一定满足要求。

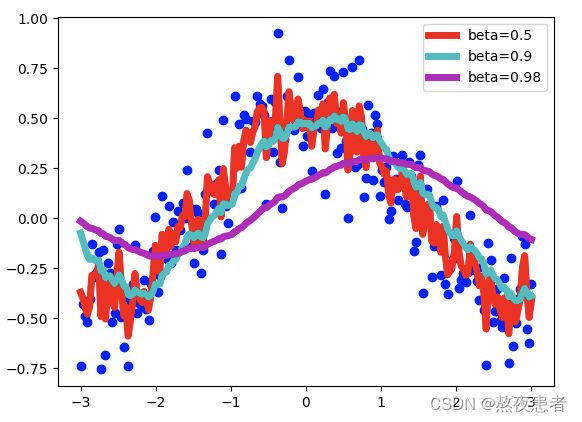
        通过老师分享得博客我们还发现，Beta 取值越小，序列 V 波动越大。因为我们平均的例子更少，因此结果与噪声数据更接近。随着 Beta 值越大，比如当 Beta = 0.98 时，我们得到的曲线会更加圆滑，但是该曲线有点向右偏移，因为我们取平均值的范围变得更大（beta = 0.98 时取值约为 50）。Beta = 0.9 时，在这两个极端间取得了很好的平衡。如下图所示:

矩阵求导

 矩阵对标量求导 Matrix-by-scalar

标量对矩阵求导 Scalar-by-matrix

看到了一个特别特别好的图，关于矩阵求导如下：

 这篇博客关于矩阵写的比较详细，我觉得一已经比较全面咯~

矩阵求导——学习笔记-CSDN博客

参考博客

指数移动平均EMA - 简书

矩阵求导常用公式_矩阵求导公式-CSDN博客

移动平均(Moving Average) - 知乎 (zhihu.com)

动量 | 机器之心 (jiqizhixin.com)