C++&&数据结构——二叉搜索树详解
目录
一,关于二叉搜索树
1.1 概念
1.2 基本结构
二,二叉搜索树接口实现
2.1 插入
2.2 查找
2.3 打印
2.4* 删除
三,二叉搜索树接口递归实现
3.1 查找
3.2 插入
3.3 删除
四,二叉搜索树的默认成员函数
五,测试代码
六,二叉搜索树的应用
6.1 KeyValue
6.2 改造二叉搜索树
6.3 测试代码
6.3.1 查找单词
6.3.2 统计水果出现的次数
一,关于二叉搜索树
1.1 概念
二叉搜索树又称二叉排序树,具有以下性质:
①一节点左子树节点的值都小于该节点的值
②一节点右子树的值都大于该节点的值
③一节点的左右子树也是二叉搜索树
简单来说就是左孩子节点比我小,右孩子节点比我大,所以以中序遍历二叉搜索树时打印的结果是从小到大的,所以二叉搜索树又被称为二叉排序树
1.2 基本结构
template
struct BSTreeNode
{
BSTreeNode* _left;
BSTreeNode* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
template
class BSTree
{
typedef BSTreeNode Node;
public:
//接口以及默认成员函数实现
private:
Node* _root = nullptr;
} 二,二叉搜索树接口实现
2.1 插入
二叉搜索树的插入不难,如果数为空直接新增根节点,如果不为空,比我小走左边,比我大走右边,走到空的时候新增节点并完成链接,如下代码和注释
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
//先找到合适的插入位置
Node* parent = nullptr; //创建parent记录cur上一个节点位置,方便后面链接
Node* cur = _root;
while (cur)
{
if (cur->_key < key) //插入的值比我大,走右边
{
parent = cur; //记录上一个位置
cur = cur->_right;
}
else if (cur->_key > key) //插入的值比我小,走左边
{
parent = cur; //记录上一个位置
cur = cur->_left;
}
else//插入的值相等,插入失败,搜索二叉树不允许数据相等
{
return false;
}
}
//找到插入位置,创建节点开始插入
cur = new Node(key);
//cur是局部变量,出了函数作用域后没了,不能直接cur赋值新节点
//所以需要把前后链接起来,这时候轮到我们的parent登场了
if (key > parent->_key) //插入的值比父节点大,走右边
{
parent->_right = cur;
}
else //插入的值比父节点小,走左边
{
parent->_left = cur;
}
return true;
}2.2 查找
由于二叉搜索树的性质,每次查找一个树的时候只需要走树的高度次就可以查到了,查找效率非常高,所以二叉搜索树还有个名称叫做二叉查找树
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)//查找的值比我大,走右边
{
cur = cur->_right;
}
else if (cur->_key > key)//查找的值比我小,走左边
{
cur = cur->_left;
}
else//查找成功
{
return true;
}
}
return false; //查找失败
}2.3 打印
打印我们以中序遍历打印,所以我们使用递归实现打印接口,如下代码:
public:
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
2.4* 删除
由于二叉搜索树关联式容器的特殊性质,删除一个节点会改变整个容器的结构与性质,所以每个关联式容器的删除操作需要做非常多的处理
对于二叉搜索树的删除,我们大致分为下面几个情况:
①:删除一个节点,需要让被删除节点的父节点指向被删除节点的左孩子节点
②:删除一个节点,需要让被删除节点的父节点指向被删除节点的右孩子节点
③:在被删除节点的右子树找一个最大值的节点替换两个节点的值,再进行删除(或者找左子树最大的点替换)
如下图
具体实现结合下面代码和注释:
bool Erase(const K& key)//难
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else//找到了,开始删除
{
// 1、左为空
if (cur->_left == nullptr)//要删除的节点的左子树为空
{
if (cur == _root)//极端情况,要干掉的是根
{
_root = cur->_right;
}
else
{
if (cur == parent->_left) //cur是父亲的左
{
parent->_left = cur->_right;
//让父亲的左指向要删除节点的右,因为cur的左为空
}
else //cur是父亲的右
{
parent->_right = cur->_right;
//让父亲的右指向要删除节点的右,因为cur的左为空
}
}
delete cur;
cur = nullptr;
}
// 2、右为空
else if (cur->_right == nullptr)//要删除的节点的右子树为空
{
if (_root == cur)//极端情况,要干掉的是根
{
_root = cur->_left;
}
else
{
if (cur == parent->_left) //cur是父亲的左
{
parent->_left = cur->_left;
//让父亲的左指向要删除节点的左,因为cur的右为空
}
else //cur是父亲的右
{
parent->_right = cur->_left;
//让父亲的右指向要删除节点的左,因为cur的右为空
}
}
delete cur;
cur = nullptr;
}
// 3、左右都不为空
else
{
// 找右子树最小节点 或 找左子树的最大节点 替代要删除的值
Node* pminRight = cur;
Node* minRight = cur->_right;
//找右树最小节点
while (minRight->_left)
{
pminRight = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key;//交换要删除的值
if (pminRight->_left == minRight)
{
pminRight->_left = minRight->_right;
}
else //这里看不懂可以结合上面的那个图中的要删除3和8的场景来理解
{
pminRight->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
//没找到,要删除的值不存在
return false;
}三,二叉搜索树接口递归实现
3.1 查找
public:
bool FindR(const K& key)///递归查找
{
return _FindR(_root, key);
}
private:
bool _FindR(Node* root,const K& key)//递归查找子函数
{
//最多找高度次,O(h) h是树的高度
if (root == nullptr) return false;
if (root->_key < key)
return _FindR(root->_right,key);
else if (root->_key > key)
return _FindR(root->_left, key);
else
return true;
}3.2 插入
实现插入子递归函数的时候,我们选择用Node* &root做函数参数,原因如下:
插入的目标是插入合适的值,并且和父亲链接起来,比如要在某个节点右边插入一个值,递归时就是 _Insert(root->right,key),我们用Node* &root之后,这个root就间接代表了上一个节点的right指针,然后我们再root = new Node(key),相当于生成一个新节点并直接赋值给父节点的右,间接完成链接,如下代码
public:
bool InsertR(const K& key)//递归插入
{
return _InsertR(_root, key);
}
private:
bool _InsertR(Node* &root, const K& key)//递归插入
{
if (root == nullptr)
{
root = new Node(key);//root是形参,所以前面用引用
return true;
}
if (root->_key < key)
return _InsertR(root->_right, key);
else if (root->_key > key)
return _InsertR(root->_left, key);
else //相等
return false;
}3.3 删除
删除我们和插入同理,用Node* &root做返回值,利用我们上面的思想完成递归实现,如下代码:
public:
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
private:
bool _EraseR(Node* &root, const K& key)
{
if (root == nullptr)
return false;
if (key > root->_key)
return _EraseR(root->_right, key);
else if (key < root->_key)
return _EraseR(root->_left, key);
else//找到了,开始删除
{
Node* del = root;
if (root->_left == nullptr)
{
//间接完成链接,这里的root在递归中可以间接认为是上一个节点的right或left,只是用了一个root引用来代替
root = root->_right;
}
else if(root->_right == nullptr)
{
root = root->_left;
}
else
{
//找右子树最小(最左)节点替换删除
Node* min = root->_right;
while (min->_left)
{
min = min->_left;
}
swap(root->_key,min->_key);
return _EraseR(root->_right, key);
}
delete del;
return true;
}
}
四,二叉搜索树的默认成员函数
public:
//由于我们自己实现了析构函数,所以编译器不会自动生成默认构造
//这条语句强制编译器生成默认构造函数
BSTree() = default;
BSTree(const BSTree& t)//拷贝构造
{
_root = _Copy(t._root);
}
~BSTree()//析构
{
_Destory(_root);
}
//t2=t1
BSTree& operator=(BSTree t)
{
swap(_root, t._root);
return *this;
}
private:
Node* _Copy(Node* root)
{
if (root == nullptr)
{
return nullptr;
}
Node* copyRoot = new Node(root->_key);
copyRoot->_left = _Copy(root->_left);
copyRoot->_right = _Copy(root->_right);
return copyRoot;
}
void _Destory(Node* &root)
{
if (root == nullptr)
{
return;
}
//先删左再删右再删根,后序
_Destory(root->_left);
_Destory(root->_right);
delete root;
root = nullptr;
} 五,测试代码
int main()
{
BSTree t1;
int a[] = { 8,3,1,10,6,4,7,14,13,4,3,4 };
for (auto e : a)
{
t1.Insert(e);
}
BSTree t2 = t1;
t1.InOrder();
t2.InOrder();
cout << "----------------" << endl;
t1.Insert(15);
t1.Insert(5);
t2.Erase(8);
t2.Erase(13);
cout << t1.Find(15) << endl;
cout << t2.Find(13) << endl;
cout << "----------------" << endl;
t1.InOrder();
t2.InOrder();
return 0;
} 六,二叉搜索树的应用
6.1 KeyValue
1,Key模型:只有Key作为关键码,结构中只需存储Key,搜索时只搜索Key
比如:给一个单词word,判断该单词是否拼写正确,方法如下
①以词库中所有单词集合中的每个单词作为Key构建一颗搜索二叉树
②在二叉搜索树中查找该单词的存在,存在则拼写正确,不存在则拼写错误
2,KV模型:每一个关键码key,都有与之对应的值Value,即
①比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文
②再比如统计单词次数,统计成功后,给定单词就可以快速找到其出现的次数,单词与其出现次数就是
6.2 改造二叉搜索树
template
struct BSTreeNode
{
BSTreeNode* _left;
BSTreeNode* _right;
K _key;
V _value;
BSTreeNode(const K& key, const V& value)
:_left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
template
class BSTree
{
typedef BSTreeNode Node;
public:
bool Insert(const K& key, const V& value)
{
if (_root == nullptr)
{
_root = new Node(key, value);
return true;
}
//找空位置插入
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)//插入的值比我大,走右边
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)//插入的值比我小,走左边
{
parent = cur;
cur = cur->_left;
}
else//插入的值相等,插入失败
{
return false;//搜索二叉树不允许数据相等
}
}
cur = new Node(key, value);//cur是局部变量,出了函数作用域后没了,需要把前后链接起来
//创建parent记录cur上一个节点位置,方便链接
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
void InOrder()
{
_InOrder(_root);
}
Node* Find(const K& key)//允许修改
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)//插入的值比我大,走右边
{
cur = cur->_right;
}
else if (cur->_key > key)//插入的值比我小,走左边
{
cur = cur->_left;
}
else//插入的值相等,查找成功
{
return cur;
}
}
return nullptr;
}
private:
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << ":" << root->_value << endl;;
_InOrder(root->_right);
}
bool FindR(const K& key)///递归查找
{
return _FindR(_root, key);
}
Node* _root = nullptr;
}; 6.3 测试代码
6.3.1 查找单词
void TestBSTree1()
{
BSTree dict;
dict.Insert("sort", "排序");
dict.Insert("left", "左边");
dict.Insert("right", "右边");
dict.Insert("string", "字符串");
dict.Insert("insert", "插入");
string str;
while (cin >> str)
{
BSTreeNode* ret = dict.Find(str);
if (ret)
{
cout << ":" << ret->_value << endl;
}
else
{
cout << "->无此单词" << endl;
}
}
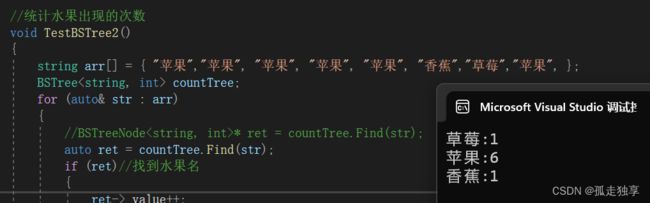
} 6.3.2 统计水果出现的次数
void TestBSTree2()
{
string arr[] = { "苹果","苹果", "苹果", "苹果", "苹果", "香蕉","草莓","苹果", };
BSTree countTree;
for (auto& str : arr)
{
//BSTreeNode* ret = countTree.Find(str);
auto ret = countTree.Find(str);
if (ret)//找到水果名
{
ret->_value++;
}
else//没有找到水果,该水果第一次出现
{
countTree.Insert(str, 1);
}
}
countTree.InOrder();
}