机器学习(十二):正则化与过拟合(附代码实例)
全文共10000余字,预计阅读时间约20~30分钟 | 满满干货,建议收藏!
一、介绍
构建一个机器学习模型并不总是一帆风顺的。可能在初步尝试之后,会发现模型在训练数据上的表现非常好,但在新的、未见过的数据上的表现却非常差。这就是所谓的过拟合问题。
过拟合是机器学习中一个常见的问题,如果模型过于复杂,就会出现模型可以记住训练数据的特定噪声,但却无法学习到有用的、通用的趋势或者模式的这种情况。此时模型最终的表现就是:在训练数据上表现得非常好,但在实际应用中,特别是在未见过的新数据上,它的性能会大打折扣,甚至非常糟糕。
为了解决过拟合问题,一个常见的方法是正则化。简单地说,正则化是一种防止模型过于复杂的策略。它可以在一定程度上保证模型的泛化性,使模型不仅在训练数据上表现良好,而且在未见过的新数据上也能有相对较好的表现。
二、过拟合和欠拟合的概念
2.1 过拟合的定义和识别
过拟合(Overfitting)是在机器学习和统计学中一个常见的现象,指的是一个模型过度学习了训练数据中的细节,包括数据中的噪声和异常点,从而导致在新的、未见过的数据上表现较差。
更深入细节一点解释:当训练数据和新数据具有规律的一致性时,才能够进行建模,而只有挖掘出贯穿始终的规律(同时影响训练数据和新数据的规律),模型才能够进行有效预测。只有在这种情况下才是有效性建模。
既然有些贯穿始终的全局规律,那就肯定存在一些只影响了一部分数据的局部规律。由于全局规律影响数据较多,因此更容易被挖掘,而局部规律只影响部分数据,因此更难被挖掘,所以从较为宽泛的角度来看,伴随着模型性能提升,也是能够捕获很多局部规律的。但是,局部规律对于新数据的预测并不能起到正面的作用,反而会影响预测结果,此时就出现模型过拟合现象。
举个生活中的例子:过拟合就像是你在准备一次考试。假设你有一本旧的考试试题集(训练数据),你通过这本书进行复习。如果你只是死记硬背这本书中的所有问题和答案(过于复杂的模型),那么在真正的考试中(测试数据),你可能会发现许多你从未见过的新问题,而你并不能很好地回答这些问题。这就是因为你过度依赖了旧的试题集,过于拟合了这些旧的数据,没有真正理解和掌握背后的知识(规律)。在机器学习中,这种情况就叫做过拟合。
2.2 欠拟合的定义和识别
在理解了过拟合后,欠拟合也就很好理解了。
欠拟合(Underfitting)指的是一个模型未能充分学习训练数据中的结构和规律,无法捕捉到数据中的关键模式,从而导致在训练数据和新的、未见过的数据上表现都较差。
更深入细节一点解释:理想的机器学习模型应该能够识别出影响数据变化的关键因素,从而能够对未见过的新数据进行有效的预测。欠拟合通常是由于模型的复杂度过低,模型的学习能力不足以理解数据的复杂性,从而不能识别出数据中的主要规律。这样的模型在训练数据上的表现通常就不好,因此,其在新数据上的表现也会很差。
举个生活中的例子:欠拟合就像是你在准备一次考试。假设你有一本旧的考试试题集(训练数据),你通过这本书进行复习。如果你只是粗略地看了一遍这本书,没有理解其中的关键问题和答案(模型复杂度过低),那么在真正的考试中(测试数据),你可能会发现自己无法回答很多问题。这就是因为你没有充分利用旧的试题集,没有理解和掌握背后的知识(规律)。在机器学习中,这种情况就叫做欠拟合。
2.3 实操:一张图理解欠拟合和过拟合
直接上代码:
import numpy as np
import matplotlib.pyplot as plt
# 设定随机数种子
np.random.seed(123)
# 创建数据
n_dots = 20
x = np.linspace(0, 1, n_dots) # 从0到1,等宽排布的20个数
y = np.sqrt(x) + 0.2*np.random.rand(n_dots) - 0.1 # 基于x生成y值,并添加一些噪声
def plot_polynomial_fit(x, y, deg):
"""
对给定数据进行多项式拟合,并绘制出原始数据、拟合结果和理想结果的图像。
参数
----------
x : ndarray
x坐标的数据
y : ndarray
y坐标的数据
deg : int
多项式的阶数
"""
# 对数据进行多项式拟合
p = np.poly1d(np.polyfit(x, y, deg))
# 生成用于绘图的数据
t = np.linspace(0, 1, 200)
# 绘制原始数据(红色圆点)、拟合结果(蓝色实线)和理想结果(红色虚线)
plt.plot(x, y, 'ro', label='Original Data')
plt.plot(t, p(t), '-', label=f'Degree {deg} Fit')
plt.plot(t, np.sqrt(t), 'r--', label='Ideal Result')
# 显示图例
plt.legend()
plt.figure(figsize=(18, 4), dpi=200)
degrees = [1, 3, 10] # 多项式的阶数
titles = ['Under Fitting', 'Fitting', 'Over Fitting'] # 图像的标题
for index, deg in enumerate(degrees):
plt.subplot(1, 3, index + 1)
plot_polynomial_fit(x, y, deg)
plt.title(titles[index], fontsize=20)
plt.show()
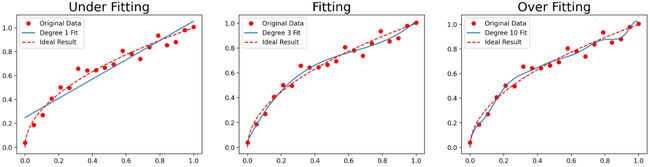
这段代码生成了三个图像,分别表示欠拟合、正常拟合和过拟合的情况。首先,生成一组含噪声的、根据二次函数生成的数据,然后分别用一次、三次和十次多项式对这组数据进行拟合,并画出拟合结果的图像,如下:
来解读一下这个图像结果:
红色圆点是原始数据,蓝色实线表示的是模型学习到的规律,红色虚线表示的是理想的结果
- 如果模型是欠拟合的,那么它的学习能力太弱,无法捕捉到数据中的所有重要规律,结果就是蓝色实线(模型的拟合结果)与红色虚线(理想结果)之间的差距较大,如"Under Fitting"的图像所示。
- 如果模型是适度拟合的,那么它的学习能力刚好,既能捕捉到数据中的重要规律,又不会被噪声所干扰,结果就是蓝色实线与红色虚线之间的差距最小,如"Fitting"的图像所示。
- 如果模型是过拟合的,那么它的学习能力太强,以至于把数据中的噪声也当作了重要规律来学习,结果就是虽然蓝色实线在红色圆点(原始数据)上的拟合效果非常好,但与红色虚线(理想结果)之间的差距却较大,如"Over Fitting"的图像所示。
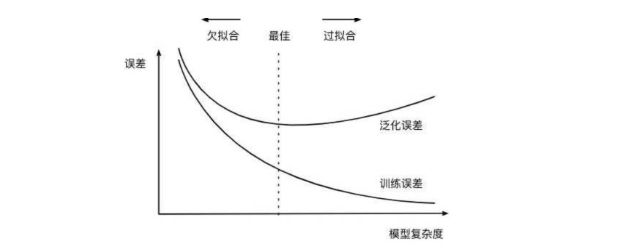
2.4 过拟合与欠拟合的平衡
先要了解两个概念:经验风险(Empirical Risk)和结构风险(Structural Risk)
在统计学习中,经验风险(Empirical Risk)和结构风险(Structural Risk)是两个关键的概念。它们主要用于评估模型的性能,以及帮助防止模型过拟合或欠拟合。
在构建损失函数求最小值的过程,其实就是依据以往经验(也就是训练数据)追求风险最小(以往数据误差最小)的过程,而在给定一组参数后计算得出的损失函数的损失值,其实这就是经验风险。
经验风险是基于训练数据计算得出的模型损失。也就是说,经验风险是模型在训练数据上的误差。最小化经验风险的目标是寻找一个函数(模型),使得它在训练集上的平均损失最小。在理想情况下,希望模型能够完全拟合训练数据,也就是说,经验风险为零。但是,完全拟合训练数据可能会导致过拟合问题,即模型在新的、未见过的数据上的性能下降。
而所谓结构风险,可以将其等价为模型复杂程度,模型越复杂,模型结构风险就越大。
所以,结构风险是对模型复杂度的一种度量。它是经验风险和模型复杂度的一个折中。在统计学习中,通常希望找到一个结构风险最小的模型。结构风险的引入是为了解决过拟合问题。一个模型如果过于复杂,可能会学习到数据中的噪声,而忽视了真正的潜在关系。这样的模型虽然在训练数据上的表现很好(经验风险低),但是在新的数据上的表现可能会很差。通过引入结构风险,可以在拟合数据和模型复杂度之间找到一个平衡。
总的来说,我们在建模的时候,通常通过最小化结构风险来选择最优的模型,这个过程就是在经验风险(数据拟合度)和模型复杂度之间找到一个最优的平衡点。在实际应用中,常用的方法如L1正则化(Lasso回归)和L2正则化(岭回归)都是基于这个原理。
三、正则化的基本概念
3.1 正则化的定义
在机器学习中,正则化(regularization)的基本形式是在模型的损失函数中添加一个正则化项(regularizer)或惩罚项(penalty term)。形式化表示如下:
总损失 = 损失函数 ( L ) + λ ∗ 正则化项 ( J ) (1) 总损失 = 损失函数(L) + λ * 正则化项(J) \tag{1} 总损失=损失函数(L)+λ∗正则化项(J)(1)
其中,L 代表损失函数,用于度量模型预测与实际标签之间的差距;J 是正则化项,用于约束模型的复杂度;λ 是正则化系数,用于调控损失函数和正则化项之间的权衡。
通过引入正则化项,能够对模型的复杂性进行限制,以防止模型过度拟合训练数据。这样,在训练过程中,模型就会在拟合数据(最小化损失函数)与保持简洁(最小化正则化项)之间找到一种平衡。
1 N ∑ i = 1 N L ( y i , f ( x i ) ) + λ J ( f ) (2) \frac{1}{N}\sum^{N}_{i=1}L(y_i,f(x_i))+\lambda J{(f)} \tag{2} N1i=1∑NL(yi,f(xi))+λJ(f)(2)
正则化项通常是模型参数的 L1 范数或 L2 范数。具体来说,添加模型参数的 L1 范数的正则化被称为 L1 正则化,而添加模型参数的 L2 范数的正则化被称为 L2 正则化。在某些情况下,可能会结合 L1 和 L2 范数,形成所谓的“弹性网络”(Elastic Net)正则化项,这是一种折中策略。
- L1 范数:也称为曼哈顿距离,它是模型参数绝对值的和。L1范数有一个有趣的特性,即它倾向于产生稀疏的权重矩阵,即其许多元素都为零。在机器学习中,这可以被用作一种自动特征选择机制。
- L2 范数:也称为欧几里得距离,它是模型参数平方和的平方根。相比之下,L2范数倾向于分散权重值,即它更倾向于平均地分配权重值,而不是集中在少数几个特征上。
接下来详细介绍几种常见的正则化技术,包括岭回归(L2正则化)、Lasso(L1正则化)和弹性网(L1和L2的结合)。
3.2 岭回归(Ridge Regression)
岭回归是线性回归的一种改进,它通过在损失函数中添加一个L2正则化项来防止过拟合。L2正则化项是模型权重参数的平方和,它的目标是限制模型权重的大小,防止模型过于复杂。
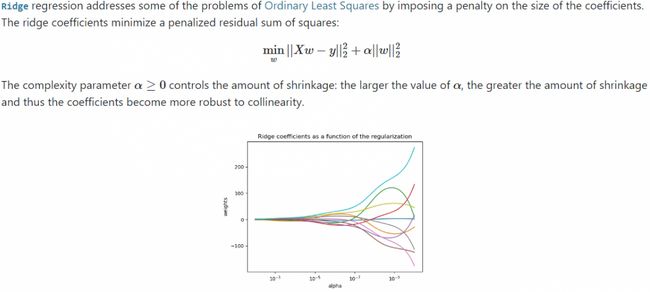
来看一下Scikit-learn官网中的描述,Ridge Regression
min w ∣ ∣ X w − y ∣ ∣ 2 2 + α ∣ ∣ w ∣ ∣ 2 2 (3) \min_{w} ||Xw-y||^2_2 + \alpha||w||^2_2 \tag{3} wmin∣∣Xw−y∣∣22+α∣∣w∣∣22(3)
这个公式的目标就是希望找到一个权重参数 w w w,使得模型的预测误差和正则化项的和最小。公式的第一部分 ∣ ∣ X w − y ∣ ∣ 2 2 ||Xw-y||^2_2 ∣∣Xw−y∣∣22 是模型的预测值与真实值之间的均方误差,这是主要优化目标。公式的第二部分 α ∣ ∣ w ∣ ∣ 2 2 α||w||^2_2 α∣∣w∣∣22 是L2正则化项, α α α 是一个超参数,用于控制正则化的强度。
选择适当的 α α α 值是岭回归模型中的一个关键步骤。 α α α 值越大,正则化的效果越强,模型的复杂度就越低,防止过拟合的能力就越强。相反, α α α 值越小,正则化的效果就越弱,模型就越可能过拟合。
总的来说,岭回归通过添加L2正则化项,平衡了模型的拟合能力和复杂度,从而有效地防止了过拟合。
3.3 Lasso回归(Lasso Regression)
Lasso(Least Absolute Shrinkage and Selection Operator)也是一种改进的线性回归方法,通过在损失函数中加入L1正则化项,来实现特征选择以及防止过拟合。L1正则化项即模型权重参数的绝对值和,其目标在于生成稀疏的权重,即许多权重为0,以此达到特征选择的目的。
来看一下Scikit-learn官网中的描述,Lasso Regression
Lasso回归的优化目标可以用以下公式表示:
min w 1 2 n s a m p l e s ∣ ∣ X w − y ∣ ∣ 2 2 + α ∣ ∣ w ∣ ∣ 1 (4) \min_{w} \frac {1}{2n_{samples}} ||Xw-y||^2_2 + \alpha||w||_1 \tag{4} wmin2nsamples1∣∣Xw−y∣∣22+α∣∣w∣∣1(4)
在此公式中,目标是找到一组权重参数 w w w,使得模型预测值和真实值之间的误差与正则化项的总和最小。公式的第一部分 ∣ ∣ X w − y ∣ ∣ 2 2 ||Xw-y||^2_2 ∣∣Xw−y∣∣22 是模型预测值与真实值之间的均方误差(还除以了样本数量的一半,保证损失不会因样本数量的变化而显著改变),这是主要的优化目标。公式的第二部分 α ∣ ∣ w ∣ ∣ 1 α||w||_1 α∣∣w∣∣1 是L1正则化项, α α α 是一个超参数,用于控制正则化的强度。
在Lasso模型中,选择合适的 α α α 值是关键步骤。 α α α 值越大,正则化效果越强,产生的稀疏权重也越多,即选择的特征越少。反之, α α α 值越小,正则化效果越弱,模型可能选择更多的特征,进而更可能产生过拟合。
总体来说,Lasso通过加入L1正则化项,在平衡模型拟合能力与复杂度的同时,有效地防止了过拟合。而且,由于其产生稀疏解的特性,Lasso也常被用于特征选择。
3.4 弹性网络(Elastic Net)
弹性网络(Elastic Net)同样是一种改进的线性回归方法,通过在损失函数中同时加入L1和L2两种正则化项,既可以实现特征选择,也可以防止过拟合。另外,对于有关联的多个特征,弹性网络倾向于选择所有这些特征,从而避免了Lasso可能随机选择相关特征中的任何一个的问题。
来看一下Scikit-learn官网中的描述,Elastic Net
弹性网络的优化目标可以用以下公式表示:
min w 1 2 n s a m p l e s ∣ ∣ X w − y ∣ ∣ 2 2 + α ρ ∣ ∣ w ∣ ∣ 1 + α ( 1 − ρ ) 2 ∣ ∣ w ∣ ∣ 2 2 (5) \min_{w} \frac {1}{2n_{samples}} ||Xw - y ||^2_2 + \alpha\rho||w||_1 + \frac {\alpha(1-\rho)}{2}||w||^2_2 \tag{5} wmin2nsamples1∣∣Xw−y∣∣22+αρ∣∣w∣∣1+2α(1−ρ)∣∣w∣∣22(5)
在此公式中,目标仍然是找到一组权重参数 w w w,使得模型预测值和真实值之间的误差与两种正则化项的总和最小。公式的第一部分 ∣ ∣ X w − y ∣ ∣ 2 2 ||Xw-y||^2_2 ∣∣Xw−y∣∣22 是模型预测值与真实值之间的均方误差(还除以了样本数量的一半,保证损失不会因样本数量的变化而显著改变),这是主要的优化目标。公式的第二部分 α ρ ∣ ∣ w ∣ ∣ 1 αρ||w||_1 αρ∣∣w∣∣1 是L1正则化项,公式的第三部分 α ( 1 − ρ ) ∣ ∣ w ∣ ∣ 2 2 α(1-ρ)||w||^2_2 α(1−ρ)∣∣w∣∣22 是L2正则化项,其中 α α α 是一个超参数,用于控制总的正则化强度,而 ρ ρ ρ 用于控制L1和L2正则化项之间的比例。
在弹性网络模型中,选择合适的 α α α 和 ρ ρ ρ 值是关键步骤。 α α α 值越大,正则化效果越强,模型复杂度越低; ρ ρ ρ 值越大,模型更倾向于进行特征选择。反之, α α α 值和 ρ ρ ρ值越小,模型可能更复杂,且更倾向于选择更多的特征。
总的来说,弹性网络通过同时加入L1和L2两种正则化项,在平衡模型拟合能力与复杂度的同时,有效地防止了过拟合。它是岭回归和Lasso回归的结合,继承了两者的优点。
3.5 为何需要正则化
一般来说,正则化核心的作用是缓解模型过拟合倾向,但是由于加入正则化项后损失函数的形体发生了变化,因此也会影响损失函数的求解过程,在某些时候,加入了正则化项之后会让损失函数的求解变得更加高效。如上面提到的岭回归,其实就是在线性回归的损失函数基础上加入了w的1-范数,而Lasso则是加入了w的2-范数。比如对于逻辑回归来说,如果加入 l 2 l2 l2正则化项,损失函数就会变成严格的凸函数。
四、实验:验证正则化缓解模型过拟合的有效性
还是使用2.3中的例子,通过一个实验看一下如何通过在模型中加入正则化项来缓解过拟合倾向。
- Step 1:在原始数据中衍生出几个特征,分别是 x 2 x^2 x2、 x 3 x^3 x3、…、 x 10 x^{10} x10,然后带入线性回归方程进行建模
from sklearn.linear_model import LinearRegression
# 设计随机数种子
np.random.seed(123)
# 创建数据
n_dots = 20
x = np.linspace(0, 1, n_dots) # 从0到1,等宽排布的20个数
y = np.sqrt(x) + 0.2*np.random.rand(n_dots) - 0.1
y.shape
x_l = []
for i in range(10):
x_temp = np.power(x, i+1).reshape(-1, 1)
x_l.append(x_temp)
X = np.concatenate(x_l, 1)
y.shape
lr = LinearRegression()
lr.fit(X, y)
# 观察建模结果
t = np.linspace(0, 1, 200)
plt.plot(x, y, 'ro', x, lr.predict(X), '-', t, np.sqrt(t), 'r--')
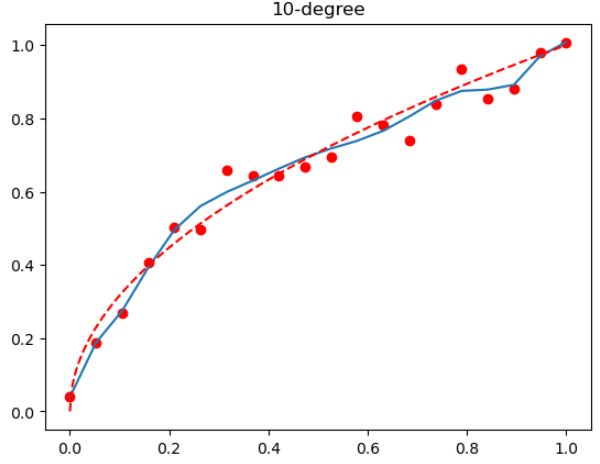
plt.title('10-degree')
看下图像:
首先,对于这个图像,需要明确的是,红色的点代表了生成的实际数据点,蓝色的线代表了使用10阶多项式特征进行线性回归后的预测结果,而红色的虚线代表了理想的预测结果。数据是基于 y = x y=\sqrt{x} y=x这个函数生成的,这是一个单调递增的平滑函数。而使用的模型是一个10阶的多项式模型,这是一个非常复杂的模型,可以拟合出复杂的非线性关系。
从图中可以看出,蓝色的线(模型预测结果)在大部分地方都非常接近红色的点(实际的数据点),甚至在一些地方,蓝色的线几乎完全覆盖了红色的点,这说明模型在训练数据上的表现非常好,几乎可以完美地拟合所有的训练数据。
然而,当观察蓝色线与红色虚线(理想的预测结果)的关系时,会发现,蓝色的线在一些地方与红色虚线有着明显的偏差。特别是在x值较大或较小的地方,蓝色线的波动非常大,明显偏离了理想的预测结果。
这就说明,模型在训练数据上的表现虽然非常好,但是在理想的预测结果上的表现却不尽人意,这是典型的过拟合现象。也就是说,模型过度地学习了训练数据中的噪声,而忽视了数据的真实分布,这导致模型在新的、未见过的数据上的表现可能会非常差。
- Step 2: 加入正则化项Ridge
针对上述的过拟合数据,尝试在线性回归的损失函数中引入正则化,来缓解10阶特征衍生后的过拟合问题。先试一下岭回归。
# 导入岭回归和Lasso
from sklearn.linear_model import Ridge,Lasso
# 参数越多、模型越简单、相同的alpha惩罚力度越大
reg_rid = Ridge(alpha=0.005)
reg_rid.fit(X, y)
# 观察惩罚效果
t = np.linspace(0, 1, 200)
plt.subplot(121)
plt.plot(x, y, 'ro', x, reg_rid.predict(X), '-', t, np.sqrt(t), 'r--')
plt.title('Ridge(alpha=0.005)')
plt.subplot(122)
plt.plot(x, y, 'ro', x, lr.predict(X), '-', t, np.sqrt(t), 'r--')
plt.title('LinearRegression')
看下图像:
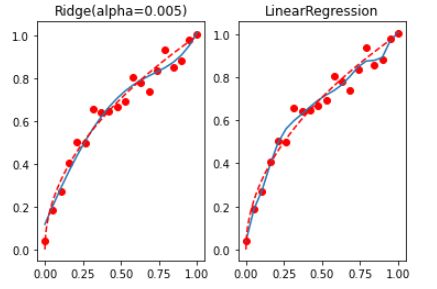
左边的图像是应用了岭回归(Ridge)之后的结果,右边的图像是应用了普通的线性回归(Linear Regression)的结果。
在上面已经解释过了,岭回归是一种改良的最小二乘估计法,通过对系数的大小施加惩罚来解决普通最小二乘法在自变量存在多重共线性时可能出现的过拟合问题。也就是说,通过引入一个α参数(也就是代码中的0.005),岭回归在尽可能保持系数总体规模不变的前提下,对系数进行调整,使得预测结果更为稳定。
从图中可以看出,使用岭回归之后,模型的预测结果(左图中的蓝色线)相较于普通的线性回归(右图中的蓝色线),在x值较大或较小的地方,偏离实际数据点(红色点)的程度有所降低,也更接近理想的预测结果(红色虚线)。这说明引入岭回归后,模型的过拟合现象得到了一定程度的缓解。
值得注意的是,岭回归的alpha参数的选择对模型的效果有很大影响,alpha过大可能会导致模型欠拟合,alpha过小又可能收效不明显。因此在实际使用中,通常需要通过交叉验证等方式来选择一个合适的alpha值。
- Step 3 :加入正则化项Lasso
直接上代码:
reg_las = Lasso(alpha=0.001)
reg_las.fit(X, y)
t = np.linspace(0, 1, 200)
plt.subplot(121)
plt.plot(x, y, 'ro', x, reg_las.predict(X), '-', t, np.sqrt(t), 'r--')
plt.title('Lasso(alpha=0.001)')
plt.subplot(122)
plt.plot(x, y, 'ro', x, lr.predict(X), '-', t, np.sqrt(t), 'r--')
plt.title('LinearRegression')
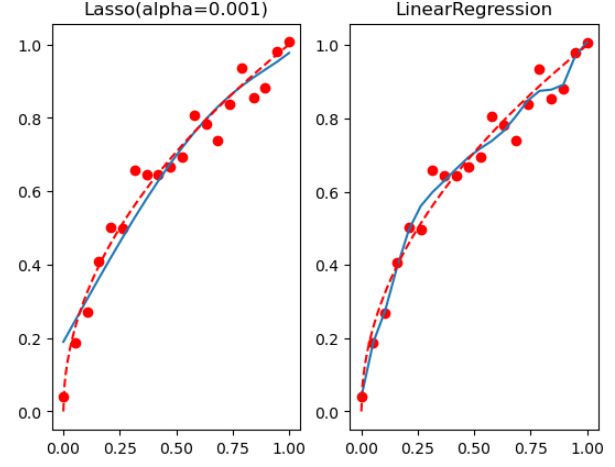
看下图像:
从图像中看到:Lasso的惩罚力度更强,并且迅速将一些参数清零,而这些被清零的参数,则代表对应的参数在实际建模过程中并不重要,从而达到特种重要性筛选的目的。在实际的建模过程中,l2正则化往往应用于缓解过拟合趋势,而l1正则化往往被用于特征筛选的场景中。
上述过程可以看出,l2缓解过拟合效果更好(相比l1正则化,l2正则化在参数筛选时过程更容易控制)
综上,分享给大家一个建模策略:
五、结语
本文深入探讨了过拟合、欠拟合及其平衡,理解了正则化的基本概念并展示了其在防止过拟合中的作用。我们通过实验验证了正则化(如岭回归、Lasso回归)在缓解过拟合和提高模型泛化能力上的有效性。总结来说,正则化是一种强大的工具,能帮助我们构建出在未知数据上表现良好的模型。
最后,感谢您阅读这篇文章!如果您觉得有所收获,别忘了点赞、收藏并关注我,这是我持续创作的动力。您有任何问题或建议,都可以在评论区留言,我会尽力回答并接受您的反馈。如果您希望了解某个特定主题,也欢迎告诉我,我会乐于创作与之相关的文章。谢谢您的支持,期待与您共同成长!
期待与您在未来的学习中共同成长。