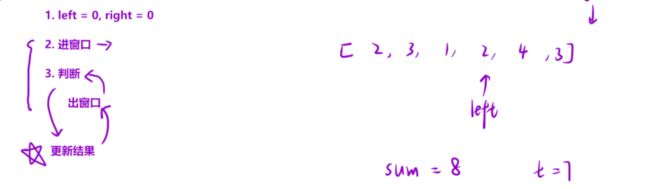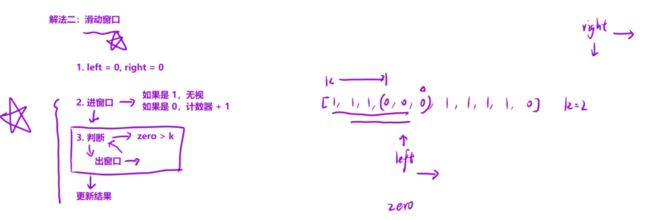算法(2)——滑动窗口
前言:
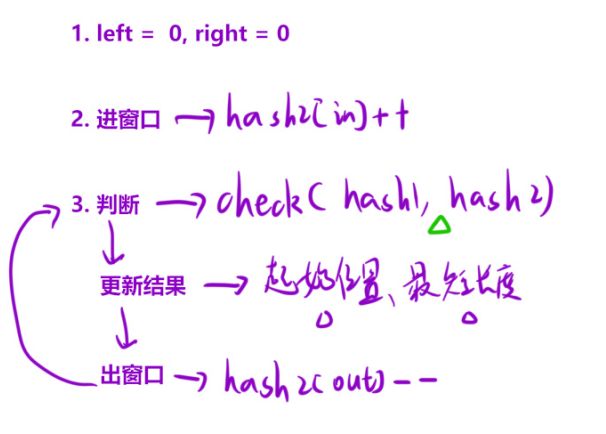
步骤及算法模板:
确定两个指针变量,left=0,right=0;
进窗口:
判断:
出窗口
更新结果
接下来我们的所用滑动窗口解决问题都需要以上几个步骤。
一、长度最小的子数组
209. 长度最小的子数组 - 力扣(LeetCode)
1、题目描述:
2、题解思路:
(1)暴力求解:「从前往后」枚举数组中的任意⼀个元素,把它当成起始位置。然后从这个「起始位置」开始,然后寻找⼀段最短的区间,使得这段区间的和「⼤于等于」⽬标值。将所有元素作为起始位置所得的结果中,找到「最⼩值」即可。
算法代码:
class Solution {
public:
int minSubArrayLen(int target, vector& nums)
{
// 记录结果
int ret = INT_MAX;
int n = nums.size();
// 枚举出所有满⾜和⼤于等于 target 的⼦数组[start, end]
// 由于是取到最⼩,因此枚举的过程中要尽量让数组的⻓度最⼩
// 枚举开始位置
for (int start = 0; start < n; start++)
{
int sum = 0; // 记录从这个位置开始的连续数组的和
// 寻找结束位置
for (int end = start; end < n; end++)
{
sum += nums[end]; // 将当前位置加上
if (sum >= target) // 当这段区间内的和满⾜条件时
{
// 更新结果,start 开头的最短区间已经找到
ret = min(ret, end - start + 1);
break;
}
}
}
// 返回最后结果
return ret == INT_MAX ? 0 : ret;
}
}; (2)滑动窗口:
由于此问题分析的对象是「⼀段连续的区间」,因此可以考虑「滑动窗」的思想来解决这道题。
让滑动窗⼝满⾜:从 i 位置开始,窗内所有元素的和⼩于 target (那么当窗内元素之和第⼀次⼤于等于⽬标值的时候,就是 i 位置开始,满⾜条件的最⼩⻓度)。
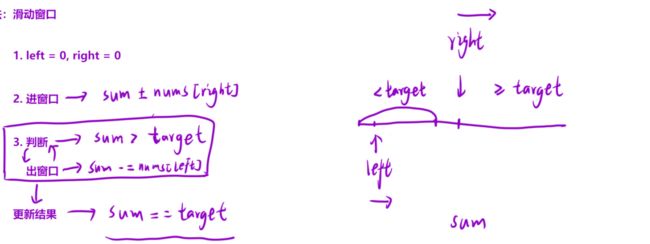
做法:将右端元素划⼊窗⼝中,统计出此时窗内元素的和:
▪ 如果窗内元素之和⼤于等于 target :更新结果,并且将左端元素划出去的同时继续判断是否满⾜条件并更新结果(因为左端元素可能很⼩,划出去之后依旧满⾜条件)
▪ 如果窗内元素之和不满⾜条件: right++ ,另下⼀个元素进⼊窗⼝。
为何滑动窗⼝可以解决问题,并且时间复杂度更低?
▪ 这个窗⼝寻找的是:以当前窗⼝最左侧元素(记为 left1 为基准,符合条件的情况。也就是在这道题中,从left1开始,满⾜区间和sum >= target时的最右侧(记为right1 )能到哪⾥。
▪ 我们既然已经找到从 left1 开始的最优的区间,那么就可以⼤胆舍去 left1 。但是如
果继续像⽅法⼀⼀样,重新开始统计第⼆个元素( left2 )往后的和,势必会有⼤量重复
的计算(因为我们在求第⼀段区间的时候,已经算出很多元素的和了,这些和是可以在计算
下次区间和的时候⽤上的)。
▪ 此时, rigth1 的作⽤就体现出来了,我们只需将 left1 这个值从 sum 中剔除。从right1 这个元素开始,往后找满⾜ left2 元素的区间(此时right1也有可能是满⾜的,因为 left1 可能很⼩。 sum 剔除掉left1 之后,依旧满⾜⼤于等于target )。这样我们就能省掉⼤量重复的计算。
▪ 这样我们不仅能解决问题,⽽且效率也会⼤⼤提升。
时间复杂度:虽然代码是两层循环,但是我们的 left 指针和 right 指针都是不回退的,两者
最多都往后移动 n 次。因此时间复杂度是O(N) 。
3、滑动窗口代码
class Solution {
public:
int minSubArrayLen(int target, vector& nums)
{
int maxlen=INT_MAX;
int left=0,right=0;
int sum=0;
while(right=target)
{
maxlen=fmin(maxlen,right-left+1);
sum-=nums[left++];
}
right++;
}
return maxlen==INT_MAX?0:maxlen;
}
}; 二、无重复字符的最长字串
3. 无重复字符的最长子串 - 力扣(LeetCode)
1、题目描述
2、题解思路:
(1)暴力求解:
枚举「从每⼀个位置」开始往后,⽆重复字符的⼦串可以到达什么位置。找出其中⻓度最⼤的即
可。
在往后寻找⽆重复⼦串能到达的位置时,可以利⽤「哈希表」统计出字符出现的频次,来判断什么
时候⼦串出现了重复元素
代码实现:
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int ret = 0; // 记录结果
int n = s.length();
// 1. 枚举从不同位置开始的最⻓重复⼦串
// 枚举起始位置
for (int i = 0; i < n; i++)
{
// 创建⼀个哈希表,统计频次
int hash[128] = { 0 };
// 寻找结束为⽌
for (int j = i; j < n; j++)
{
hash[s[j]]++; // 统计字符出现的频次
if (hash[s[j]] > 1) // 如果出现重复的
break;
// 如果没有重复,就更新 ret
ret = max(ret, j - i + 1);
}
}
// 2. 返回结果
return ret;
}
};(2)滑动窗口实现:
研究的对象依旧是⼀段连续的区间,因此继续使⽤「滑动窗⼝」思想来优化。
让滑动窗⼝满⾜:窗⼝内所有元素都是不重复的。做法:右端元素 ch 进⼊窗⼝的时候,哈希表统计这个字符的频次:
▪ 如果这个字符出现的频次超过 1 ,说明窗⼝内有重复元素,那么就从左侧开始划出窗⼝,直到 ch 这个元素的频次变为 1 ,然后再更新结果。
▪ 如果没有超过 1 ,说明当前窗⼝没有重复元素,可以直接更新结果
代码实现:
class Solution {
public:
int lengthOfLongestSubstring(string s)
{
int left=0,right=0;
int hash[128]={0};
int maxlen=0;
while(s.size()>right)
{
hash[s[right]]++;
while(hash[s[right]]>1)
{
hash[s[left]]--;
left++;
}
maxlen=max(maxlen,right-left+1);
right++;
}
return maxlen;
}
};三、最大连续1的个数Ⅲ
1004. 最大连续1的个数 III - 力扣(LeetCode)
1、题目描述:
2、题解思路:
不要去想怎么翻转,不要把问题想的很复杂,这道题的结果⽆⾮就是⼀段连续的1 中间塞了 k 个 0 嘛。
因此,我们可以把问题转化成:求数组中⼀段最⻓的连续区间,要求这段区间内0的个数不超过 k 个。
3、代码实现:
class Solution {
public:
int longestOnes(vector& nums, int k)
{
int left=0,right=0;
int zero=0;
int maxlen=0;
while(nums.size()>right)
{
if(nums[right]==0) zero++;
while(k 四、将x减到0的最⼩操作数
1658. 将 x 减到 0 的最小操作数 - 力扣(LeetCode)
1、题目描述:
2、题解思路:
题⽬要求的是数组「左端+右端」两段连续的、和为 x 的最短数组,信息量稍微多⼀些,不易理清
思路;我们可以转化成求数组内⼀段连续的、和为 sum(nums) - x 的最⻓数组。此时,就是熟
悉的「滑动窗⼝」问题了。
3、代码实现:
class Solution {
public:
int minOperations(vector& nums, int x)
{
int sum=0;
for(auto e:nums) sum+=e;
int target=sum-x;
if(target<0) return -1;
int left=0,right=0;
int ret=-1;
int tmp=0;
while(righttarget)
{
tmp-=nums[left];
left++;
}
if(target==tmp)
{
ret=max(ret,right-left+1);
}
right++;
}
if(ret==-1)
{
return ret;
}
else
{
return nums.size()-ret;
}
}
}; 五、⽔果成篮
904. 水果成篮 - 力扣(LeetCode)
1、题目描述:
2、题解思路:
让滑动窗⼝满⾜:窗⼝内⽔果的种类只有两种。
做法:右端⽔果进⼊窗⼝的时候,⽤哈希表统计这个⽔果的频次。这个⽔果进来后,判断哈希表的
⼤⼩:
▪ 如果⼤⼩超过2:说明窗⼝内⽔果种类超过了两种。那么就从左侧开始依次将⽔果划出窗⼝,直到哈希表的⼤⼩⼩于等于2,然后更新结果;
▪ 如果没有超过2,说明当前窗⼝内⽔果的种类不超过两种,直接更新结果ret。
3、算法代码:
class Solution{
public:
int totalFruit(vector& fruits)
{
int left=0,right=0;
int hash[100001]={0};
int ret=0,kinds=0;
while(fruits.size()>right)
{
if(hash[fruits[right]]==0) kinds+=1;
hash[fruits[right]]++;
while(kinds>2)
{
hash[fruits[left]]--;
if(hash[fruits[left]]==0) kinds-=1;
left++;
}
ret=fmax(ret,right-left+1);
right++;
}
return ret;
}
}; 六、找到字符串中所有字⺟异位词
438. 找到字符串中所有字母异位词 - 力扣(LeetCode)
1、题目描述:
2、算法思路:
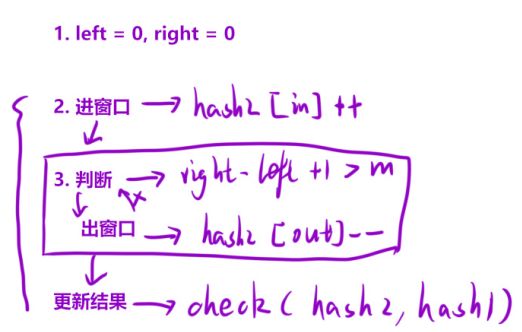
◦ 因为字符串 p 的异位词的⻓度⼀定与字符串 p 的⻓度相同,所以我们可以在字符串 s 中构
造⼀个⻓度为与字符串 p 的⻓度相同的滑动窗⼝,并在滑动中维护窗⼝中每种字⺟的数量;
◦ 当窗⼝中每种字⺟的数量与字符串 p 中每种字⺟的数量相同时,则说明当前窗⼝为字符串p 的异位词;
◦ 因此可以⽤两个⼤⼩为26 的数组来模拟哈希表,⼀个来保存 s 中的⼦串每个字符出现的个数,另⼀个来保存 p 中每⼀个字符出现的个数。这样就能判断两个串是否是异位词。
3、算法代码:
class Solution {
public:
vector findAnagrams(string s, string p)
{
vector ret;
int hash1[26]={0};
int hash2[26]={0};
for(auto ch:p) hash1[ch-'a']++;
int m=p.size();
for(int left=0,right=0,count=0;rightm)
{
char out=s[left];
left++;
if(hash2[out-'a']-- <= hash1[out-'a']) count--;
}
if(count==m)
{
ret.push_back(left);
}
}
return ret;
}
}; 七、串联所有单词的⼦串
30. 串联所有单词的子串 - 力扣(LeetCode)
1、题目描述:
words[i]和s由小写英文字母组成
2、题解思路:
如果我们把每⼀个单词看成⼀个⼀个字⺟,问题就变成了找到「字符串中所有的字⺟异位词」。⽆
⾮就是之前处理的对象是⼀个⼀个的字符,我们这⾥处理的对象是⼀个⼀个的单词。
3、算法代码:
class Solution {
public:
vector findSubstring(string s, vector& words)
{
vector ret;
unordered_map hash1; //保存words所有单词的频次
for(auto& ch:words) hash1[ch]++;
int len=words[0].size(),m=words.size();
for(int i=0;i hash2; //维护窗口内单词的频次
for(int left=i,right=i,count=0;right+len<=s.size();right+=len)
{
//进窗口+维护
string in =s.substr(right,len); //截取长度为len的字符串
hash2[in]++;
if(hash1.count(in)&&hash2[in]<=hash1[in]) count++;
//判断
if(right-left+1>len*m)
{
//出窗口+维护
string out =s.substr(left,len);
if(hash1.count(out)&&hash2[out]<=hash1[out]) count--;
hash2[out]--;
left+=len;
}
//更新结果
if(count==m)
{
ret.push_back(left);
}
}
}
return ret;
}
}; 八、最⼩覆盖⼦串
76. 最小覆盖子串 - 力扣(LeetCode)
1、题目描述:
2、算法思路:
◦ 研究对象是连续的区间,因此可以尝试使⽤滑动窗⼝的思想来解决。
◦ 如何判断当前窗⼝内的所有字符是符合要求的呢?
我们可以使⽤两个哈希表,其中⼀个将⽬标串的信息统计起来,另⼀个哈希表动态的维护窗⼝
内字符串的信息。
当动态哈希表中包含⽬标串中所有的字符,并且对应的个数都不⼩于⽬标串的哈希表中各个字
符的个数,那么当前的窗⼝就是⼀种可⾏的⽅案。
3、算法代码:
class Solution {
public:
string minWindow(string s, string t)
{
int hash1[128]={0};
int kinds=0;
for(auto ch:t) if(hash1[ch]++==0) kinds++;
int hash2[128]={0};
int minlen=INT_MAX,begin=-1;
for(int left=0,right=0,count=0;right