【机器学习】线性模型-线性支持向量机

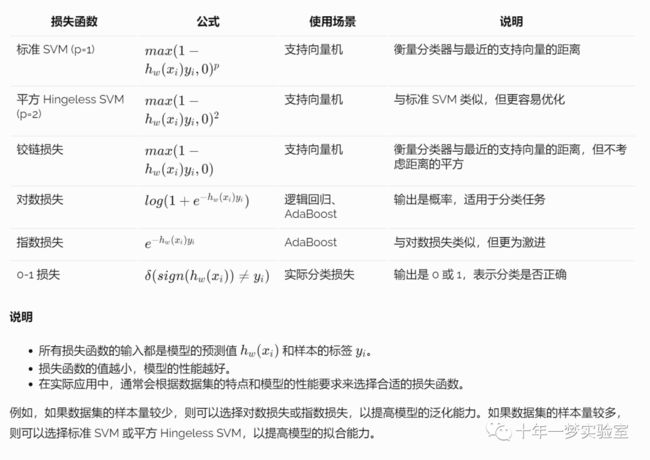
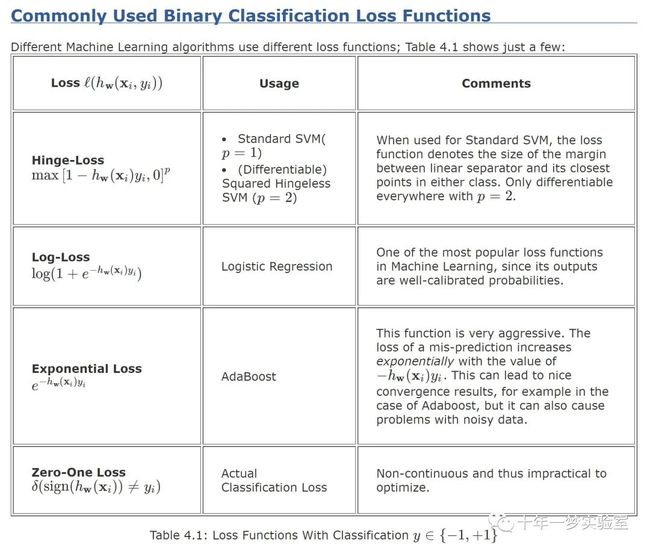
一、常用二分类损失函数

二、三种不同的正则化器（L2-正则化，L1-正则化和Lp-范数）的性质

三、线性支持向量机原理

L1正则化L1-loss SVC原问题

L2正则化L2-loss SVC原问题

L2正则化SVC对偶问题

L1正则化L2-loss SVC原问题

多分类线性支持向量机

四、示例代码（LinearSVC 、SVC）

在本练习中，我们将使用支持向量机（SVM）构建垃圾邮件分类器。我们将从一些简单的2D数据集上的支持向量机开始，看看它们是如何工作的。然后，我们将对一组原始电子邮件进行一些预处理工作，并使用SVM对处理后的电子邮件构建分类器，以确定它们是否是垃圾邮件。

我们要做的第一件事是查看一个简单的二维数据集，并了解线性SVM如何针对不同的C值在数据集上工作（类似于线性/逻辑回归中的正则化项）。让我们加载数据。

# 导入 numpy, pandas, matplotlib, seaborn, scipy 等常用的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat
#%matplotlib inline


# 从 data/ex6data1.mat 文件中加载数据
raw_data = loadmat('data/ex6data1.mat')
#print('raw_data:{0}'.format(raw_data))


# 将数据转换为 pandas 的 DataFrame 格式，方便处理
data = pd.DataFrame(raw_data['X'], columns=['X1', 'X2'])
data['y'] = raw_data['y']


# 根据 y 的值，将数据分为正类和负类
positive = data[data['y'].isin([1])]
negative = data[data['y'].isin([0])]


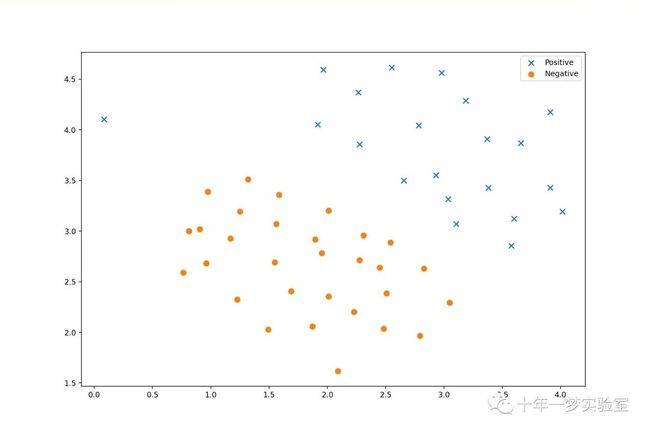
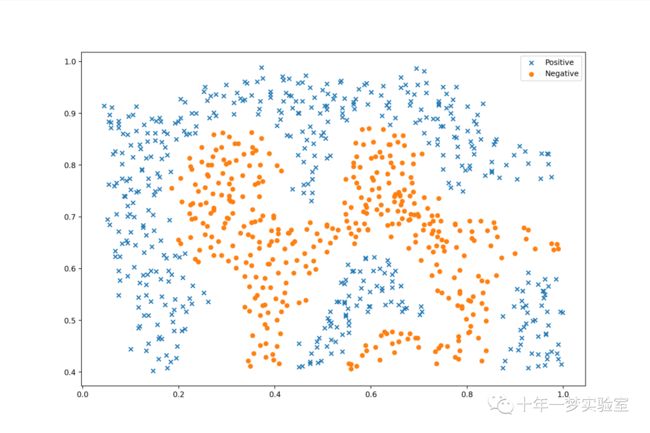
# 使用 matplotlib 画出数据的散点图，用不同的符号和颜色表示不同的类别
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['X1'], positive['X2'], s=50, marker='x', label='Positive')
ax.scatter(negative['X1'], negative['X2'], s=50, marker='o', label='Negative')
ax.legend()
#plt.show()

我们将其可视化为散点图，其中类标签由符号表示（+表示正数，。表示负数）。

请注意，有一个异常的正样本与其他样本不同。这些类仍然是线性可分离的，但它是一个非常紧密的配合。我们将训练线性支持向量机来学习类边界。在本练习中，我们的任务不是从头开始实现SVM，因此我将使用scikit-learn中内置的SVM

# 导入 sklearn 库中的 svm 模块，用于实现支持向量机算法
from sklearn import svm
# 创建一个线性核的支持向量机分类器对象，设置 C=1, 损失函数为 hinge, 最大迭代次数为 10000
svc = svm.LinearSVC(dual=True,C=1, loss='hinge', max_iter=10000)
print('ex6data1   svc  :{0}'.format(svc))
# ex6data1   svc  :LinearSVC(C=1, dual=True, loss='hinge', max_iter=10000)
# LinearSVC(C=1, class_weight=None, dual=True, fit_intercept=True,
#    intercept_scaling=1, loss='hinge', max_iter=1000, multi_class='ovr',
#    penalty='l2', random_state=None, tol=0.0001, verbose=0)


# 对于第一个实验，我们将使用C=1并看看它的表现如何。
# 使用数据的 X1 和 X2 特征，以及 y 标签，训练支持向量机分类器
svc.fit(data[['X1', 'X2']], data['y'])
# 计算分类器在训练数据上的准确率
#svc.score(data[['X1', 'X2']], data['y'])
print('ex6data1 C=1  svc.score on train set: {0}'.format(svc.score(data[['X1', 'X2']], data['y'])))
# ex6data1 C=1  svc.score on train set: 0.9803921568627451


# 看来它对异常值进行了错误分类。让我们看看当C值更大时会发生什么。
# 创建另一个线性核的支持向量机分类器对象，设置 C=100, 损失函数为 hinge, 最大迭代次数为 100000
svc2 = svm.LinearSVC(dual=True,C=100, loss='hinge', max_iter=100000) # ConvergenceWarning: Liblinear failed to converge, increase the number of iterations
# 使用数据的 X1 和 X2 特征，以及 y 标签，训练支持向量机分类器
svc2.fit(data[['X1', 'X2']], data['y'])
# 计算分类器在训练数据上的准确率
#svc2.score(data[['X1', 'X2']], data['y'])
print('ex6data1 C=100 svc2.score on train set: {0}'.format(svc2.score(data[['X1', 'X2']], data['y'])))
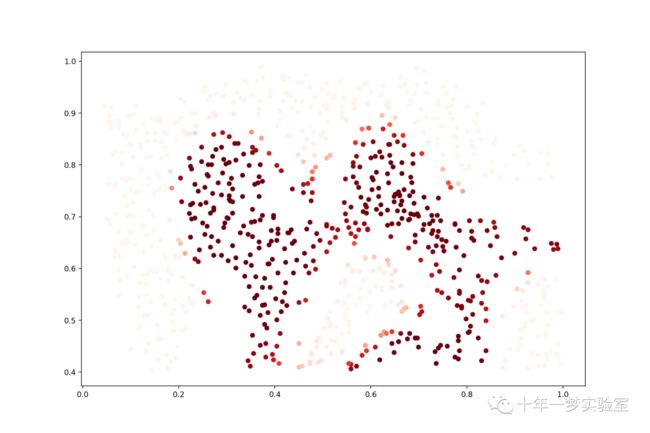
# ex6data1 C=100 svc2.score on train set: 0.9803921568627451

通过增加C的值，我们创建了一个不再自然适合数据的决策边界。我们可以通过查看每个类预测的置信水平来可视化这一点，这是点与超平面距离的函数。（max_iter =1000 没有收敛到最优解，需要调大）

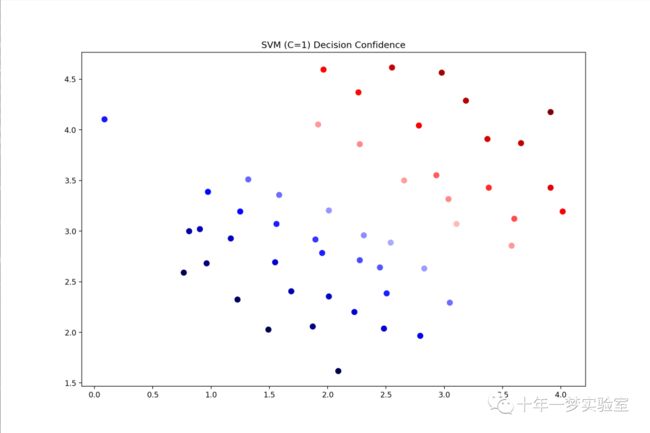
# 计算数据的 SVC 1 置信度，即分类器的决策函数值
data['SVM 1 Confidence'] = svc.decision_function(data[['X1', 'X2']])


# 使用 matplotlib 画出数据的散点图，用不同的颜色表示不同的 SVM 1 置信度
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(data['X1'], data['X2'], s=50, c=data['SVM 1 Confidence'], cmap='seismic')
ax.set_title('SVM (C=1) Decision Confidence')
#plt.show()

# 计算数据的 SVC 2 置信度，即分类器的决策函数值. 颜色值
data['SVM 2 Confidence'] = svc2.decision_function(data[['X1', 'X2']])


# 使用 matplotlib 画出数据的散点图，用不同的颜色表示不同的 SVM 2 置信度
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(data['X1'], data['X2'], s=50, c=data['SVM 2 Confidence'], cmap='seismic')
ax.set_title('SVM (C=100) Decision Confidence')
#plt.show()

差异有点微妙，但看看边界附近点的颜色。

现在我们将从线性支持向量机转向能够使用核进行非线性分类的支持向量机。

# 从 data/ex6data2.mat 文件中加载数据   863x2  863*1
raw_data = loadmat('data/ex6data2.mat')


# 将数据转换为 pandas 的 DataFrame 格式，方便处理
data = pd.DataFrame(raw_data['X'], columns=['X1', 'X2'])
data['y'] = raw_data['y']


# 根据 y 的值，将数据分为正类和负类
positive = data[data['y'].isin([1])]
negative = data[data['y'].isin([0])]


# 使用 matplotlib 画出数据的散点图，用不同的符号和颜色表示不同的类别
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['X1'], positive['X2'], s=30, marker='x', label='Positive')
ax.scatter(negative['X1'], negative['X2'], s=30, marker='o', label='Negative')
ax.legend()
#plt.show()

# 创建一个高斯核的支持向量机分类器对象，设置 C=100, gamma=10, probability=True
svc = svm.SVC(C=100, gamma=10, probability=True)
#svc
print('ex6data2 C=100 svc  :{0}'.format(svc))
# ex6data2 C=100 svc  :SVC(C=100, gamma=10, probability=True)


# 使用数据的 X1 和 X2 特征，以及 y 标签，训练支持向量机分类器
svc.fit(data[['X1', 'X2']], data['y'])
# 计算分类器在训练数据上的准确率
#svc.score(data[['X1', 'X2']], data['y'])
print('ex6data2 C=100 svc.score on train set: {0}'.format(svc.score(data[['X1', 'X2']], data['y'])))
# ex6data2 C=100 svc.score on train set: 0.9698725376593279


# 计算数据的概率，即分类器的预测概率值
data['Probability'] = svc.predict_proba(data[['X1', 'X2']])[:,0]
#print('分类器预测概率值 ：{0}'.format(data['Probability']))




# 使用 matplotlib 画出数据的散点图，用不同的颜色表示不同的概率
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(data['X1'], data['X2'], s=30, c=data['Probability'], cmap='Reds')
plt.show()

对于第三个数据集，我们提供了训练集和验证集，并负责根据验证集性能寻找SVM模型的最佳超参数。尽管我们可以使用scikit-learn 的内置网格搜索来轻松完成此操作，但本着遵循练习指示的精神，我们将从头开始实现一个简单的网格搜索。

############# 从 data/ex6data3.mat 文件中加载数据
raw_data = loadmat('data/ex6data3.mat')


# 提取数据中的 X, Xval, y, yval   测试集和验证集
X = raw_data['X']
Xval = raw_data['Xval']
y = raw_data['y'].ravel()
yval = raw_data['yval'].ravel()


# 定义一些候选的 C 和 gamma 值
C_values = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]
gamma_values = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]


# 初始化最佳的分数和参数
best_score = 0
best_params = {'C': None, 'gamma': None}


# 遍历所有的 C 和 gamma 的组合，找出最优的参数
for C in C_values:
    for gamma in gamma_values:
        # 创建一个高斯核的支持向量机分类器对象，设置 C 和 gamma
        svc = svm.SVC(C=C, gamma=gamma)
        # 使用数据的 X 和 y，训练支持向量机分类器
        svc.fit(X, y)
        # 计算分类器在验证数据上的准确率
        score = svc.score(Xval, yval)
        
        # 如果分数比之前的最佳分数高，就更新最佳分数和参数
        if score > best_score:
            best_score = score
            best_params['C'] = C
            best_params['gamma'] = gamma


# 输出最佳的分数和参数
#best_score, best_params
print('ex6data3  best_score={0}'.format(best_score))
#ex6data3  best_score=0.965
print('ex6data3  best_params={0}'.format(best_params))
# ex6data3  best_params={'C': 0.3, 'gamma': 100}

现在我们将继续练习的第二部分。在这一部分中，我们的目标是使用SVM 构建垃圾邮件过滤器。在练习文本中，有一项任务涉及一些文本预处理，以便以适合SVM处理的格式获取数据。然而，该任务非常简单（将单词映射到为练习提供的字典中的ID），并且其余的预处理步骤（例如HTML删除、词干提取、规范化等）已经完成。我不会重现这些预处理步骤，而是直接跳到机器学习任务，该任务涉及从预处理的训练和测试数据集（包括转换为单词出现向量的垃圾邮件和非垃圾邮件）构建分类器。

# 从 data/spamTrain.mat 和 data/spamTest.mat 文件中加载数据
spam_train = loadmat('data/spamTrain.mat') # 4000*1899   4000*1
spam_test = loadmat('data/spamTest.mat') #1000*1899  1000*1   


spam_train


# 提取数据中的 X, Xtest, y, ytest
X = spam_train['X']
Xtest = spam_test['Xtest']
y = spam_train['y'].ravel()
ytest = spam_test['ytest'].ravel()


# 查看数据的维度
X.shape, y.shape, Xtest.shape, ytest.shape
print('X.shape :{0} , y.shape :{1}, Xtest.shape :{2}, ytest.shape :{3}'.format(X.shape, y.shape, Xtest.shape, ytest.shape))
# X.shape :(4000, 1899) , y.shape :(4000,), Xtest.shape :(1000, 1899), ytest.shape :(1000,)

每个文档都已转换为具有1，899个维度的向量，对应于词汇表中的1，899个单词。这些值是二进制的，指示文档中是否存在该单词。此时，训练和评估只是拟合测试分类器的问题。

# 创建一个线性核的支持向量机分类器对象
svc = svm.SVC()
# 使用数据的 X 和 y，训练支持向量机分类器
svc.fit(X, y)
# 计算分类器在训练数据上的准确率  Training accuracy = 99.32%
print('Training accuracy = {0}%'.format(np.round(svc.score(X, y) * 100, 2)))
# 计算分类器在测试数据上的准确率 Test accuracy = 98.7%
print('Test accuracy = {0}%'.format(np.round(svc.score(Xtest, ytest) * 100, 2)))

此结果是使用默认参数的结果。我们可能可以通过一些参数调整将其提高一点。

五、sklearn.svm.LinearSVC  与 sklearn.svm.SVC对比

参考网址

(1) LIBLINEAR算法解读 - 知乎. https://zhuanlan.zhihu.com/p/464186750.
(2) sklearn.svm.LinearSVC — scikit-learn 1.3.2 documentation. https://scikit-learn.org/stable/modules/generated/sklearn.svm.LinearSVC.html.
(3) 四、线性支持向量机算法(LinearSVC，Linear Support Vector Classification)（有监督学习 .... https://blog.csdn.net/qq_41264055/article/details/133121451.
(4) sklearn.svm.LinearSVR-scikit-learn中文社区. https://scikit-learn.org.cn/view/777.html.
(5) undefined. https://welts.xyz.

(6) https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote10.html  损失函数与分类

(7) https://scikit-learn.org/stable/modules/generated/sklearn.svm.LinearSVC.html 

(8) https://www.mit.edu/~9.520/fall14/slides/class06/class06_RLSSVM.pdf

(9) https://zhuanlan.zhihu.com/p/66933242

(10)https://scikit-learn.org.cn/view/777.html  sklearn.svm.LinearSVR 中文

(11) https://scikit-learn.org.cn/view/91.html   中文社区 1.12 多类和多标签算法

(12) https://github.com/Kaslanarian/liblinear-sc-reading LIBLINEAR理论解读

(13) https://welts.xyz/2022/02/03/crammer_singer/  多分类线性支持向量机与坐标下降法求解其对偶问题

(14) https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/

(15) https://github.com/jdwittenauer/ipython-notebooks/blob/master/notebooks/ml/ML-Exercise6.ipynb