3.1 数字类型及操作 | Python语言程序设计(嵩天)
文章目录
- 课程简介
- 第三章 基本数据类型
-
- 3.1 数字类型及操作
-
- 3.1.1 整数类型
- 3.1.2 浮点数类型
- 3.1.3 复数类型
- 3.1.4数值运算操作符
- 3.1.5 数值运算函数
- 小结
- 版权说明
课程简介
计算机是运算工具,更是创新平台,高效有趣地利用计算机需要更简洁实用的编程语言。Python简洁却强大、简单却专业,它是当今世界最受欢迎的编程语言,学好它终身受用。请跟随我们,学习并掌握Python语言,一起动起来,站在风口、享受创新!
—— 课程团队
![]()
MOOC课程:
Python语言程序设计(嵩天 、黄天羽 、礼欣)
北京理工大学
课程视频地址:
课程视频-B站
授课目标:
本课程适合如下教学目标:
- 程序设计入门课:面向各层次各专业大学在校生、部分优秀高中生,作为程序设计入门课程
- 体系化编程基础:面向拟构建坚实编程能力的自学者,作为不断奋斗的参考在线课程
- Python科目备考:面向全国计算机等级考试二级Python科目的备考考生,作为在线备考资源
- 再试一次的尝试:面向拟放弃计算机或编程学习的学习者,作为再试一次的课程资源,学不会这门课学再放弃不迟…
第三章 基本数据类型
- 3.1 数字类型及操作
- 3.2 实例3: 天天向上的力量
- 3.3 字符串类型及操作
- 3.4 模块2: time库的使用
- 3.5 实例4: 文本进度条
3.1 数字类型及操作
- 数字类型:
- 整数类型
- 浮点数类型
- 复数类型
- 操作:
- 数值运算操作符
- 数值运算函数
3.1.1 整数类型
- 整数无限制
- pow() 函数
- 4 种进制表示形式
与数学中整数的概念一致
可正可负,没有取值范围限制
pow(x,y)函数
用于计算 x x x 的 y y y 次幂,即 x y x^y xy ,想算多大算多大。
例:计算 2 100 2^{100} 2100
#计算2的100次方
pow(2,100)
例:计算 2 2 15 2^{2^{15}} 2215
#计算2的(2的15次方)次方
pow(2,pow(2,15))
Python提供 4 种进制形式来表示整数
- 十进制,例如:1010, 99, -217
- 二进制,以0b或0B开头,例如:0b010, -0B101
- 八进制,以0o或0O开头,例如:0o123, -0O456
- 十六进制,以0x或0X开头,例如:0x9a, -0X89
3.1.2 浮点数类型
- 取值范围和精度基本无限制
- 运算存在不确定尾数,用
round()函数做四舍五入- 科学计数法的表示
与数学中实数的概念一致。
- 指带有小数点及小数的数字
- 浮点数取值范围和小数精度都存在限制,但在常规计算中可忽略不计。
- Python 中的浮点数取值范围数量级约为: − 1 0 308 -10^{308} −10308 ~ 1 0 308 10^{308} 10308,精度数量级为: 1 0 − 16 10^{-16} 10−16
浮点数间运算存在不确定尾数,不是bug(很多编程语言中都存在这一特性)
计算机中所有数字都是用二进制来表示的。在 Python 语言中用53位的二进制来表示一个浮点数的小数部分,约 1 0 16 10^{16} 1016 ,由于计算机中的二进制与十进制之间不存在严格对等关系。
例如: 0.1 在用二进制表示时,就是一个无限的小数,计算机只能截取其中的53位使之无限接近 0.1 ,因此,这并不是真正意义上的等于 0.1 。
>>> 0.1 + 0.3
0.4
>>> 0.1 + 0.2
0.30000000000000004 #计算结果中产生了不确定尾数
round()函数-
用
round()函数做四舍五入运算,解决以上问题。
round(x, d)对参数x进行四舍五入,参数d为小数截取位数。 -
用
round()函数来判断浮点数运算与浮点数之间的比较关系。
浮点数间做比较运算时,可用round()函数进行辅助,
-
不确定尾数一般发生在二进制数的第 1 0 16 10^{16} 1016 位左右,或在十进制小数的第 16 16 16 位上下才会产生。
>>> 0.1+0.2 == 0.3
False #计算结果中产生了不确定尾数,说明 0.1 + 0.2 ≠ 0.3
>>>
>>> round(0.1+0.2,1) == 0.3
True #浮点数间做比较运算时,因不确定尾数的存在,常用 round() 函数进行辅助判断
>>>
在 Python 程序中,连续的两个等号==,是表示“等于”的判断符号。
科学计数法的表示方式
Python 用字母 e 或 E 作为幂的符号,以 10 为基数,可用于表示较大或较小的浮点数。表示格式如下:
<a>e<b>
e 表示 a × 1 0 b a × 10^b a×10b
例:
4.3e-3 值为 0.0043 ,即 4.3 × 1 0 − 3 4.3 × 10^{-3} 4.3×10−3
9.6E5 值为 960000.0,即 9.6 × 1 0 5 9.6 × 10^5 9.6×105
3.1.3 复数类型
与数学中复数的概念一致
在众多编程语言中,只有Python语言提供了复数类型。
复数类型在常规的计算机编程中很少使用,但它却是进行空间变换、尤其与复变函数相关的科学体系中最常用的一种数字类型。
如果 x 2 = − 1 x^2 = -1 x2=−1 ,那 x x x 的值是什么?
任何数的平方都不能是负数,所以“ x 2 = − 1 x^2 = -1 x2=−1 ” 一定不是实数。
定义一个数量叫做 j j j ,它是一个单位,
定义 j = ( − 1 ) j=\sqrt{(-1)} j=(−1) ,以此为基础构建出新的数学体系——复数
- a + b j a+bj a+bj 为复数
- a a a 为实数部分,也叫实部
- b j bj bj 整体为虚数部分,其中的 b b b 是虚部
例: z = 1.23 e − 4 + 5.6 e + 89 j z=1.23e-4+5.6e+89j z=1.23e−4+5.6e+89j
用 z.real 获得 实部 1.23 e − 4 1.23e-4 1.23e−4 ,用 z.imag 获得 虚部 5.6 e + 89 j 5.6e+89j 5.6e+89j
3.1.4数值运算操作符
操作符是完成运算的一种符号体系
Python 内置的数值运算操作符(9 个)
| 操作符 | 描述 |
|---|---|
| x + y | 加,x 与 y 之和 |
| x – y | 减,x 与 y 之差 |
| x * y | 乘,x 与 y 之积 |
| x / y | 除,x 与 y 之商 10/3 结果是 3.3333333333333335 |
| x // y | 整数除,x 与 y 之整数商 10//3 结果是 3 |
| + x | x 本身 |
| - y | x 的负值 |
| x % y | 余数,模运算 10%3 结果是 1 |
| x ** y | 幂运算,x 的 y 次幂, x y x^y xy。当y是小数时,开方运算 10**0.5 结果是 10 \sqrt{10} 10 。即:可用幂运算实现开方运算 |
二元操作符有对应的增强赋值操作符
增强赋值操作符:+=, -=, *=, /=, //=, %=, **=
二元操作符:+, -, *, /, //, %, **
用 op 表示 二元操作符
x op= y 等价于 x = x op y
注意:
op 与二元操作符之间没有空格。
增强赋值操作符 将获得的结果写入变量 x 中,简化了代码表达。
数字类型的关系
-
类型间的混合运算
类型间可进行混合运算,生成结果为"最宽"类型-
三种数字类型(整数、浮点数、复数)之间存在一种逐渐“扩展”或“变宽”的关系:
整数 -> 浮点数 -> 复数 -
整数可看作浮点数的特殊形式,即,将整数看作小数部分为零的情况。
浮点数可看作复数的特殊情况,即,将浮点数看作复数虚部为零的情况
-
-
基本规则
- ① 整数之间运算,若数学意义上的结果是整数,则输出结果为整数。
- ② 整数之间运算,若数学意义上的结果是小数,则输出结果为浮点数。
- ③整数和浮点数做混合运算,则输出结果为浮点数。
- ④整数或浮点数与复数做混合运算,则输出结果为复数。
例: 123 + 4.0 = 127.0 123+4.0=127.0 123+4.0=127.0
123 + 4.0 = 127.0 # 整数 + 浮点数 = 浮点数
127 后面加上 .0 的表示意义:
若计算结果是浮点数,就需要特别注意经过运算时可能产生的不确定尾数。
3.1.5 数值运算函数
一些以函数形式提供的数值运算功能
Python 内置的数值运算函数(6 个)
-
abs(x) 绝对值,x的绝对值
-
divmod(x,y) 商余,(x//y, x%y),同时输出商和余数
-
pow(x, y[, z]) 幂余,(x**y)%z,[…]表示参数z可省略
-
round(x[, d]) 四舍五入,d是保留小数位数,默认值为0
-
max(x1,x2, … ,xn) 最大值,返回x1,x2, … ,xn中的最大值,n不限
-
min(x1,x2, … ,xn) 最小值,返回x1,x2, … ,xn中的最小值,n不限
特例:
-
从 Python 语法角度看计算:
pow(3, pow(3, 999)) % 10000
计算机会先求出幂运算结果,再进行模运算,普通计算机无法完成该任务。 -
使用内置数字运算函数
pow(x, y[z])计算:pow(3, pow(3, 999), 10000)
在幂运算的同时进行模运算,并能快速计算出结果。
Python 内置的数字类型转换函数(3 个)
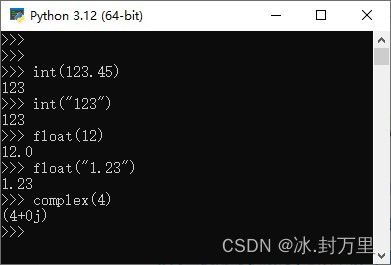
-
int(x) 将 x 变成整数,舍弃小数部分
-
float(x) 将 x 变成浮点数,增加小数部分
-
complex(x) 将 x 变成复数,增加虚数部分
小结
整数类型的无限范围及4种进制表示
浮点数类型的近似无限范围、小尾数及科学计数法
+、-、*、/、//、%、**、二元增强赋值操作符
内置的数值运算函数:abs()、divmod()、pow()、round()、max()、min()
内置的数字类型转换函数:int()、float()、complex()
版权说明
![]()