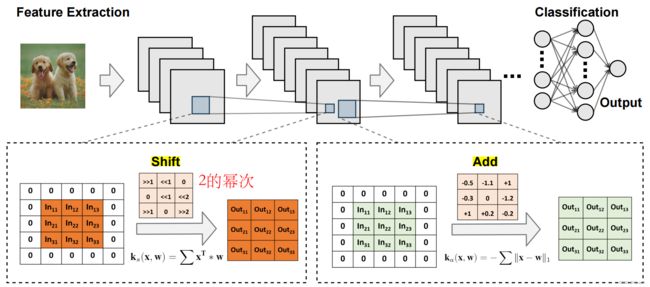
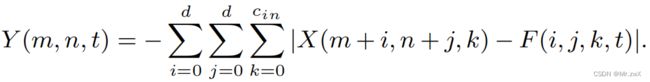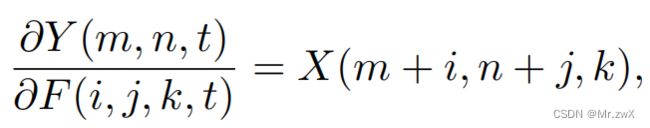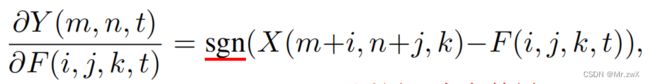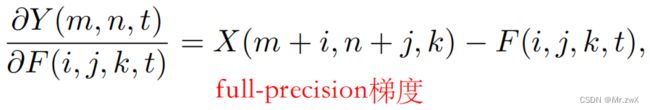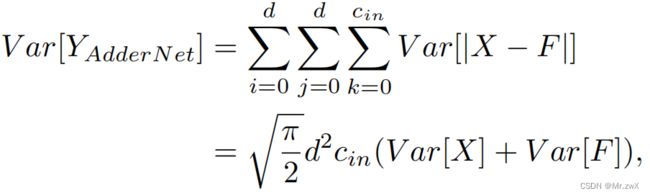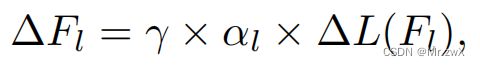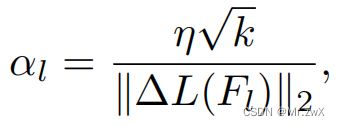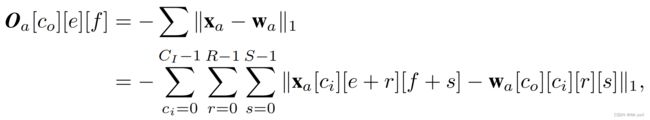去掉乘法运算的加法移位神经网络架构
[CVPR 2020] AdderNet: Do We Really Need Multiplications in Deep Learning?
代码:https://github.com/huawei-noah/AdderNet/tree/master
核心贡献
- 用filter与input feature之间的L1-范数距离作为“卷积层”的输出
- 为了提升模型性能,提出全精度梯度的反向传播方法
- 根据不同层的梯度级数,提出自适应学习率策略
研究动机
- 加法远小于乘法的计算开销,L1-距离(加法)对硬件非常友好
- BNN效率高,但是性能难以保证,同时训练不稳定,收敛慢
- 几乎没有工作尝试用其他更高效的仅包含加法的相似性度量函数来取代卷积
其中, S S S是相似度(距离)衡量指标,如果定义为内积,则是传统卷积算法。
从而,计算中不存在任何乘法计算。Adder层的输出都是负的,所以网络中引入batch normalization(BN)层和激活函数层。注意BN层虽然有乘法,但是其开销相比于卷积可以忽略不计。
为什么可以将卷积替换为加法?作者的解释是第一个公式类似于图像匹配领域,在这个领域中 S S S可以被替换为不同的函数,因此在卷积神经网络中把内积换成L1-距离也是很自然的想法。
其中,sgn是符号函数。但是,signSGD几乎没有采取最陡的下降方向,随着维度的增长,下降方向只会变得更糟,所以不适用于大参数量的模型优化。
在形式上就是去掉了signSGD的sgn函数。
为了避免梯度爆炸的问题,提出将梯度裁剪到[-1, 1]范围内:

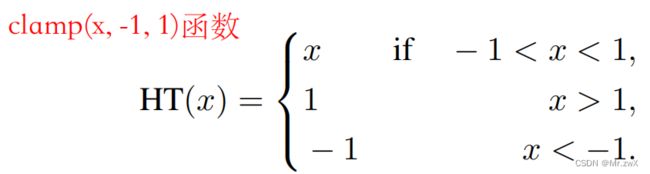
CNN中filter的方差非常小,所以Y的方差很小;而AdderNet中Y的方差则非常大。
这个梯度的级数应该很小,本文对不同层weight梯度的L2-norm值进行了统计:

发现AdderNet的梯度确实相比于CNN非常小,这会严重减慢filter更新的过程。
一种最直接的思路就是采用更大的学习率,本文发现不同层的梯度值差异很大,所以为了考虑不同层的filter情况,提出了不同层的自适应学习率。
其中, γ \gamma γ是全局学习率, ∆ L ( F l ) ∆L(F_l) ∆L(Fl)是第 l l l层filter梯度, α l \alpha_l αl是对应层的本地学习率。
k k k是 F l F_l Fl中元素的数量, η \eta η是超参数。于是,不同adder层中的filter可以用几乎相同的step进行更新。
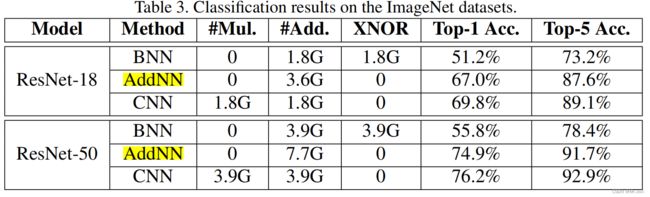
可以看到,AdderNet在三个CNN模型上都掉点很少,并且省去了所以乘法,也没有BNN中的XNOR操作,只是有了更多的加法,效率应该显著提高。
核心代码
Adder层:
X_col = torch.nn.functional.unfold(X.view(1, -1, h_x, w_x), h_filter, dilation=1, padding=padding, stride=stride).view(n_x, -1, h_out*w_out)
X_col = X_col.permute(1,2,0).contiguous().view(X_col.size(1),-1)
W_col = W.view(n_filters, -1)
output = -(W_col.unsqueeze(2)-X_col.unsqueeze(0)).abs().sum(1)
反向传播优化:
grad_W_col = ((X_col.unsqueeze(0)-W_col.unsqueeze(2))*grad_output.unsqueeze(1)).sum(2)
grad_W_col = grad_W_col/grad_W_col.norm(p=2).clamp(min=1e-12)*math.sqrt(W_col.size(1)*W_col.size(0))/5
grad_X_col = (-(X_col.unsqueeze(0)-W_col.unsqueeze(2)).clamp(-1,1)*grad_output.unsqueeze(1)).sum(0)
[NeurIPS 2020] ShiftAddNet: A Hardware-Inspired Deep Network
代码:https://github.com/GATECH-EIC/ShiftAddNet
主要贡献
- 受到硬件设计的启发,提出bit-shift和add操作,ShiftAddNet具有完全表达能力和超高效率
- 设计训练推理算法,利用这两个操作的不同的粒度级别,研究ShiftAddNet在训练效率和精度之间的权衡,例如,冻结所有的位移层
研究动机
- Shift和add比乘法更高效
- Add层学习的小粒度特征,shift层被认为可以提取大粒度特征提取
冻结shift层
冻结ShiftAddNet中的shift层意味着 s , p s, p s,p在初始化后一样,然后进一步剪枝冻结的shift层以保留必要的大粒度anchor weight。
[NeurIPS 2023] ShiftAddViT: Mixture of Multiplication Primitives Towards Efficient Vision Transformers
代码:https://github.com/GATECH-EIC/ShiftAddViT
核心贡献
- 用混合互补的乘法原语(shift和add)来重参数化预训练ViT(无需从头训练),得到“乘法降低”网络ShiftAddViT。Attention中所有乘法都被add kernel重参数化,剩下的线性层和MLP被shift kernel重参数化
- 提出混合专家框架(MoE)维持重参数化后的ViT,其中每个专家都代表一个乘法或它的原语,比如移位。根据给定输入token的重要性,会激活合适的专家,例如,对重要token用乘法,并对不那么重要的token用移位
- 在MoE中引入延迟感知和负载均衡的损失函数,动态地分配输入token给每个专家,这确保了分配的token数量与专家的处理速度相一致,显著减少了同步时间
研究动机
- 乘法可以被替换为shift和add
- 如果重参数化ViT?ShiftAddNet是级联结构,需要双倍的层数/参数Shift和add层的CUDA内核比PyTorch在CUDA上的训练和推理慢得多
- 如何保持重参数化后ViT的性能?对于ViT,当图像被分割成不重叠token时,我们可以利用输入token之间固有的自适应敏感性。原则上包含目标对象的基本token需要使用更强大的乘法来处理(这个idea和token merging很类似)
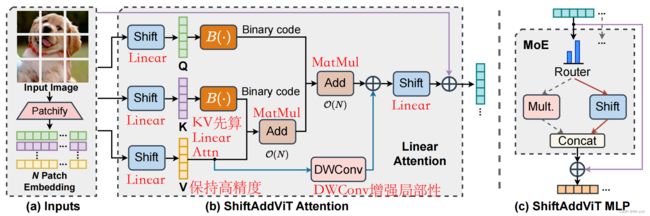
总体框架设计
- 对于attention,将4个linear层和2个矩阵乘转换为shift和add层
- 对于MLP,直接替换为shift层会大幅降低准确率,因此设计了MoE框架合并乘法原语的混合,如乘法和移位
- 注意:linear->shift, MatMul->add
Attention重参数化
考虑二值量化,于是两个矩阵之间的乘累加(MAC)运算将高效的加法运算所取代。
将 ( Q K ) V (QK)V (QK)V改为 Q ( K V ) Q(KV) Q(KV)以实现线性复杂度, Q , K Q, K Q,K进行二值量化,而更敏感的 V V V保持高精度,并插入轻量级的DWConv增强模型局部性。
可以看到,实际上ShiftAddViT就是把浮点数乘法简化为了2的幂次的移位运算和二值的加法运算。
![]()
其中, s , P s, P s,P都是可以训练的。
敏感性分析
在attention层应用线性注意力、add或shift对ViT准确性影响不大,但是在MLP层应用shift影响很明显!同时,使MLP更高效,对能源效率有很大贡献,因此需要考虑新的MLP重参数化方法。
MLP重参数化
MLP同样主导ViT的延迟,所以用shift层替换MLP的linear层,但是性能下降明显,所以提出MoE来提升其性能。
MoE框架
-
假设: 假设重要但敏感的输入token,需要更强大的网络,否则会显著精度下降
-
乘法原语的混合: 考虑两种专家(乘法和shift)。根据router中gate值 p i = G ( x ) p_i=G(x) pi=G(x),每个输入token表示 x x x将被传递给一位专家,输出定义如下:

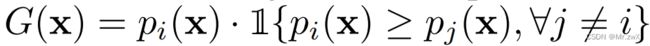
其中, n , E i n, E_i n,Ei表示专家数和第 i i i个专家。 -
延迟感知和负载均衡的损失函数: MoE框架的关键是设计一个router函数,以平衡所有专家有更高的准确性和更低的延迟。乘法高性能但慢,shift快但低性能,如何协调每个专家的工作负荷,以减少同步时间?

其中,SCV表示给定分布对专家的平方变异系数(本文没介绍)。通过设计的损失函数,可以满足(1)所有专家都收到gate值的预期加权和;(2)为所有专家分配预期的输入token数。