深大算法设计与分析实验三——回溯法解决地图填色问题
源代码:
深大算法实验三——回溯法解决地图填色问题代码-C/C++文档类资源-CSDN下载
目录
问题描述
背景知识:
问题描述:
开始实验!!!
回溯法算法思想:
在地图填色当中的回溯法
效率提升方法
最少剩余量选择(MRV)
度最大选择(DH)
颜色选择:最少约束值
向前检验
约束传播
颜色轮寻
数据分析
实验结论
问题描述
背景知识:
为地图或其他由不同区域组成的图形着色时,相邻国家/地区不能使用相同的颜色。 我们可能还想使用尽可能少的不同颜色进行填涂。一些简单的“地图”(例如棋盘)仅需要两种颜色(黑白),但是大多数复杂的地图需要更多颜色。
每张地图包含四个相互连接的国家时,它们至少需要四种颜色。1852年,植物学专业的学生弗朗西斯·古思里(Francis Guthrie)于1852年首次提出“四色问题”。他观察到四种颜色似乎足以满足他尝试的任何地图填色问题,但他无法找到适用于所有地图的证明。这个问题被称为四色问题。长期以来,数学家无法证明四种颜色就够了,或者无法找到需要四种以上颜色的地图。直到1976年德国数学家沃尔夫冈·哈肯(Wolfgang Haken)(生于1928年)和肯尼斯·阿佩尔(Kenneth Appel,1932年-2013年)使用计算机证明了四色定理,他们将无数种可能的地图缩减为1936种特殊情况,每种情况都由一台计算机进行了总计超过1000个小时的检查。
他们因此工作获得了美国数学学会富尔克森奖。在1990年,哈肯(Haken)成为伊利诺伊大学(University of Illinois)高级研究中心的成员,他现在是该大学的名誉教授。
四色定理是第一个使用计算机证明的著名数学定理,此后变得越来越普遍,争议也越来越小 更快的计算机和更高效的算法意味着今天您可以在几个小时内在笔记本电脑上证明四种颜色定理。
问题描述:
我们可以将地图转换为平面图,每个地区变成一个节点,相邻地区用边连接,我们要为这个图形的顶点着色,并且两个顶点通过边连接时必须具有不同的颜色。附件是给出的地图数据,请针对三个地图数据尝试分别使用5个(le450_5a),15个(le450_15b),25个(le450_25a)颜色为地图着色。
开始实验!!!
-
回溯法算法思想:
回溯法他的本质上是一种穷举法,他是将所有的解按照一定结构进行排列,在进行搜索的一种方法。一般的解空间为一种树状结构,树的每一层填写一个解,当该解可行时则遍历该节点的枝,如果当该解不可行时,则不遍历下面的枝。
回溯法可以使用递归的思想进行实现,以下是回溯法的框架。
我们可以看到if就是判断是否完成整个的遍历,下面的for循环就是对该节点的解进行尝试,选择选择列表中的解,然后进行递归,递归完毕后则将选择撤销。
如果使用最普通的回溯法来寻找第一个数据集的解,则过很长的时间都无法遍历出来。所以我们必须要提高算法的效率。
回溯法提高的效率有两种,一个是在选择节点和选择解的顺序,通过这两点,提前试错,在结构树的上端知道错误。另一个是加大剪枝的力度,在判断解是否可行时尽量得出否的结果。
-
在地图填色当中的回溯法
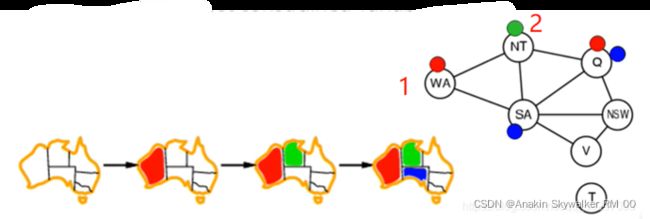
在地图填色当中,每一个节点就是一个需要填涂的区域,解就是填涂的颜色,下图可以完整的呈现回溯法在地图填色问题上的使用,此图是使用3种颜色进行填涂。
在地图填色当中,我们可以将每一块区域看成是一个节点,相邻的区域用领边进行连接,那么上图的地图用图的方式表示就为以下情况:
节点一节点之间的关系我使用邻接矩阵的方式进行存储,这样可以使数据十分的直观。
整个回溯法的伪代码如下:
if s>=vecNum
Print
else
for i=1 to colorNum
if place(vec,i)==true
backtrack (vec+1,s)
end if
end for
end else
-
效率提升方法
最少剩余量选择(MRV)
最少剩余量选择是优先选择剩余可填涂颜色最少的节点。如何判断该节点的剩余可填涂颜色,我使用了每个节点对应的颜色数组进行判断。这样操作的原因是可选择颜色少的节点进行填涂后可以加大这条解是正确的几率。
如下图,在填涂完WA、NT节点后,准备选择填涂SA节点还是Q节点。我们可以看到SA节点只有一个颜色可以填涂,Q节点有两个节点进行填涂,于是我们优先选择SA节点填涂。
若我们先填涂Q节点并且选择了蓝色,在下一次选择节点中在SA处是不可行的,则需要回溯,时间将会浪费。若我们选择了先填涂SA的蓝色,则Q只有一个红色可以填涂,此举便是正确的选择方法。
度最大选择(DH)
度最大选择是优先选择度最多的节点,因为度数越多的节点受到其他节点的约束就越大,若填涂完周围的节点再填涂该节点发现不正确时则要浪费很多时间,若优先填涂了该节点那么可以影响周围节点可选择的颜色。
如下图,SA节点的度数是最多的,所以优先填涂SA,则他周围的邻接节点只能选择其余的两种颜色。如果填涂了周围的其余节点并使用了三种颜色,则填涂到SA节点时会发现无法填涂,之前所填涂的颜色花费的时间就浪费了。
度最大选择需要放在MRV方法之后,也就是说再MRV中剩余量最少且相同的几个节点当中选择出来度最大的节点进行优先填涂。
在填涂一个节点时,需要减去相邻节点的个数,因为是对没有填涂节点进行操作的,并在回溯时进行恢复。
颜色选择:最少约束值
在确定节点后我们需要选择颜色。在选择颜色时我们需要选择该节点影响周围节点剩余颜色最少的颜色,也就是说要尽量不要选择周围节点可使用的颜色。在前方我已经介绍过,每一个节点有对应的剩余可选择颜色数组,当该节点选择某一颜色时们会根据邻接矩阵来进行计数,如果相邻节点的剩余颜色中有该颜色,则进行计数,最后优先选择计数最少的颜色。
如下图,填涂完WA和NT节点后,在填涂Q节点时,若选择红色,则相邻节点剩余的颜色中,只有NSW的剩余颜色有红色,那么红色计数为1。若选择蓝色,相邻节点当中SA和NSW的剩余颜色都有蓝色,则蓝色的计数为2。所以我们优先选择红色。
向前检验
向前检验是每一个节点都有对应的可选择颜色,当某节点选择了一个颜色之后,则将邻接节点的可选颜色中,将该颜色删除。如果在删除的过程中发现删除后已经没有颜色可以填涂,那么就放弃该节点的那一颜色。这种方法可以提前知道某节点的选择是否正确,可以提前试错。也就是加大了剪枝操作。
如下图,当WA选择红色以后就将WA周围相邻节点的红色给删除。在后面若NT填涂了蓝色,则SA没有颜色填涂,所以放弃该颜色进行回溯。
约束传播
约束传播实际上相当于二次向前探查,就是说当剩余颜色只有一个颜色时,就直接填涂那个颜色,并将该节点影响的其余节点的剩余颜色删除。
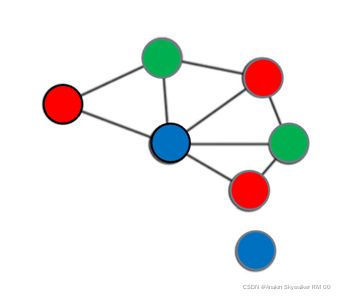
如下图,SA只剩下了一个颜色可以填涂,则将SA填涂为蓝色,那么将相邻的NSW和NT的蓝色删除,我们发现NT节点没有颜色可以填涂了,说明了Q节点填涂绿色是不可取的。
约束传播我们可以用递归的方法,一直将剩余一个颜色的节点进行填涂,直到没有单独的节点。但是这种回溯对于图比较复杂的情况下,这也会是一种回溯,会使时间变慢。
颜色轮寻
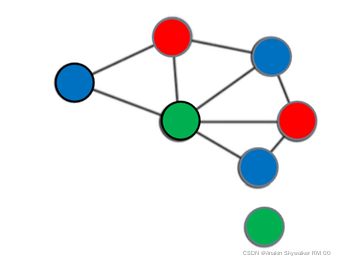
颜色轮寻是知道一组解后,可以将其余的颜色轮换,得到另外的一组解。假如有红蓝两种颜色可以填图,当知道一组解后可以将解的红色和蓝色进行交换,得到另一组解。
如下图的两个解,只是将相应的颜色进行了交换,所以说可以只遍历一遍就可以得到另外的几组解。
如何实现呢?首先若有n中颜色,则遍历出一组解后就可以得到n!个解。当填涂颜色时,使用的时之前没有使用过的颜色话,将该节点其余没有使用过的颜色进行删除,不遍历其余的颜色。
如下图,当第一个节点使用红色时,则不遍历绿色和蓝色了,以此类推。
数据分析
数据集1使用5色,数据集2使用15色,数据集3使用25色。
1. 使用上述所有方式并且使用递归调用的约束传播结果。
我们可以看到第一个数据集可以跑到0.369s,但是另外的两个数据集无法得出结果,这是因为在约束传播递归时数据比较复杂,需要花费很多的时间。
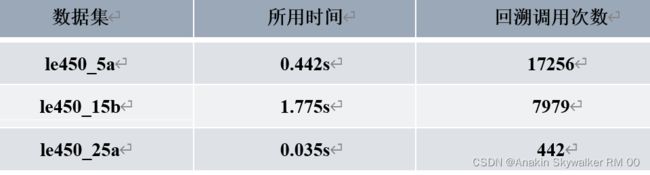
2. 不使用约束传播方法,也就是不使用二次向前探查
可以得出结果,但是速度比较慢,并且回溯调用次数增多。
3. 使用一次约束传播,也就是进行向前探查两次
速度明显提升并且回溯调用次数减少,说明剪枝十分的有效果。但是第一个数据集无法达到第一次那么的快速。
4. 进一步探查。
将填涂完一个颜色将边数减1 改为加1。
可以观察到,第一个数据集十分的快速,进入到了0.289秒的时间,并且回溯调用次数明显减少。但是其余的两个数据集无法得出结果。这说明了这种特殊情况只适用与数据集1。
5. 使用随机数观察
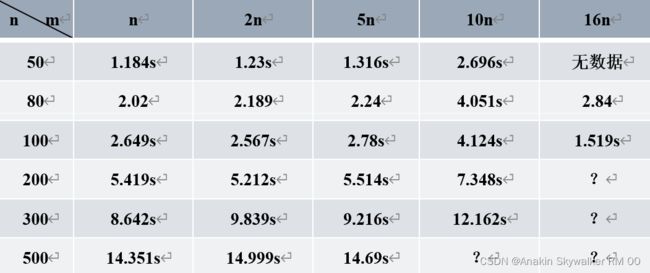
N为节点数,m为边数。颜色数:8,此为运行100亿个结果就停止的时间。
在边数与节点数比例相同时,节点数越大,所用时间越多。当节点数相同时,则在一定范围内边数越多,所用时间越长,但是到达一定程度时,边数越大所用时间越短(节点数是80和100得出的结论)
实验结论
本次实验熟悉了回溯法并且体验了使用回溯法怎么进行剪枝操作,对于回溯法有了更深层次的了解,也懂得了剪枝和选择节点对于回溯法提升效率的重要性。从一开始数据集1无法跑出来到200多秒,47秒到现在的接近0.3秒可以明显地体会到优化的重要性。其中,颜色轮寻的方法是十分有效并且十分快速的,可以直接将数据集从47秒提升到0.3秒,有效的进行了剪枝。