C++刷题周记(番外篇)——单调栈模板

单调栈实际上只有两类问题：求一个数左边第一个小于他的数/求一个数右边第一个大于他的数

以上两类问题，归根结底也是同一问题，所以我们可以使用统一模板解决

其主要有四种情况，以下为伪代码(st为所创建的单调栈，nums为目标数组，res为结果数组)。

其区别主要在于遍历数组的顺序，以及while循环中出栈的控制条件不同

求 “左边第一个小于” 时，单调栈需要为单调递减栈(从 栈顶往栈底 看)

求 “右边第一个大于” 时，单调栈需要为单调递增栈(从 栈顶往栈底 看)

是否为严格单调则需要根据题意与题目测试用例进行具体分析

①.寻找一个数左边第一个小于它的数

// 求“左边第一个小于”时，正序遍历数组
for(int i = 0;i < nums.size();i++){
    // 维护一个单调递减栈    
    // 具体分析是否为严格单调 若可以为不严格单调则无需取等
    // 当不满足nums[i] > st.top()的递减性质时，循环出栈直至满足
    while(!st.empty() && nums[i] <= st.top()){
        st.pop();
    }
    if(!st.empty()){
        res[i] = st.top();
    }
    // 根据题意对未找到的数的结果赋值
    else res[i] = -1;
    st.push(nums[i]);
}

②.寻找一个数左边第一个小于它的数的下标

// 求“左边第一个小于”时，正序遍历数组
for(int i = 0;i < nums.size();i++){
    // 维护一个单调递减栈    
    // 具体分析是否为严格单调 若可以为不严格单调则无需取等
    // 当不满足nums[i] > st.top()的递减性质时，循环出栈直至满足
    while(!st.empty() && nums[i] <= nums[st.top()]){
        st.pop();
    }
    if(!st.empty()){
        res[i] = nums[st.top()];
    }
    // 根据题意对未找到的数的结果赋值
    else res[i] = -1;
    st.push(i);
}

③.寻找一个数右边第一个大于它的数

// 求“右边第一个大于”时，倒序遍历数组
for(int i = nums.size()-1; i >= 0; i--){
    // 维护单调递增栈
    // 具体分析是否为严格单调 若可以为不严格单调则无需取等
    // 当不满足nums[i] < st.top()的递增性质时，循环出栈直至满足
    while(!st.empty() && nums[i] >= st.top()){
        st.pop();
    }
    if(!st.empty()){
        res[i] = st.top();
    }
    // 根据题意对未找到的数的结果赋值
    else res[i] = -1;
    st.push(nums[i]);
}

④.寻找一个数右边第一个大于它的数的下标

// 求“右边第一个大于”时，倒序遍历数组
for(int i = nums.size()-1; i >= 0; i--){
    // 维护单调递增栈
    // 具体分析是否为严格单调 若可以为不严格单调则无需取等
    // 当不满足nums[i] < st.top()的递增性质时，循环出栈直至满足
    while(!st.empty() && nums[i] >= nums[st.top()]){
        st.pop();
    }
    if(!st.empty()){
        res[i] = nums[st.top()];
    }
    // 根据题意对未找到的数的结果赋值
    else res[i] = -1;
    st.push(i);
}

我看到了一个比较好的形象化理解，出处为：力扣

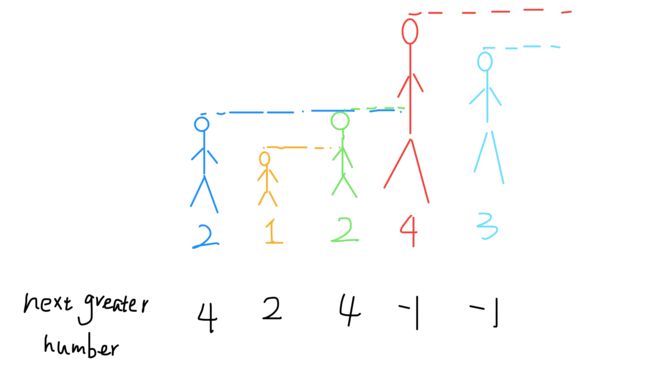
这个问题可以这样抽象思考：把数组的元素想象成并列站立的人，元素大小想象成人的身高。这些人面对你站成一列，如何求元素「2」的 Next Greater Number 呢？

很简单，如果能够看到元素「2」，那么他后面可见的第一个人就是「2」的 Next Greater Number，因为比「2」小的元素身高不够，都被「2」挡住了，第一个露出来的就是答案。

题目：

模板题：Acwing 830

应用：Leetcode 739 每日温度   

Leetcode 1944 队列中可以看到的人数

Leetcode 496 下一个更大元素 I

Leetcode 503 下一个更大元素 II

以上题目均可以使用模板解决，这里不再赘述，只展开说lc 503中涉及到循环数组的处理技巧

本题是可以使用笨方法，将数组复制扩容为原长度2倍后套用模板解决，只是会浪费空间

可以考虑通过对遍历时指针翻倍，而在遍历时使用指针与数组原长取余作为下标，从而达到循环数组的效果。

    vector nextGreaterElements(vector& nums) {
        stack st;
        int len = nums.size();
        vector res(len);
        // 笨方法:将数组复制扩容为原长度2倍 套模板
        // 小技巧:指针翻倍 遍历时下标取余 来节约空间
        for(int i = len * 2 - 1;i >= 0;i--){
            // 注意 套模板尽量维持单调栈为严格单调递增/减 的
            while(!st.empty() &&  nums[i % len] >= st.top()){
                st.pop();
            }
            if(!st.empty()){
                res[i % len] = st.top();
            }
            else res[i % len] = -1;
            st.push(nums[i % len]);
        }
        return res;
    }

参考资料：

深入浅出单调栈与单调队列_Iareges的博客-CSDN博客

难度题：

42. 接雨水

求左/右第一个大于i的下标，可维护一个单调递增栈(从栈顶往栈底看)

可参考题解：代码随想录 （之后再来填坑）

如出一辙做法的一道题：84. 柱状图中最大的矩形

求左/右第一个小于i的下标，维护单调递减栈

需要注意数组本来就是完全单调时的特判。

85. 最大矩形

本题可以原封不动地使用之前的方法，转化到二维空间解决