链表相关算法

刷题汇总

第一章 数组
第二章 链表

---

---

前言

链表是一种通过指针串联在一起的线性结构，每一个节点由两部分组成，一个是数据域一个是指针域（存放指向下一个节点的指针），最后一个节点的指针域指向null（空指针的意思）。

链接的入口节点称为链表的头结点也就是head。

如图所示： 链表

C/C++定义的链表节点：

// 单链表
struct ListNode {
    int val;  // 节点上存储的元素
    ListNode *next;  // 指向下一个节点的指针
    ListNode(int x) : val(x), next(NULL) {}  // 节点的构造函数
};

删除节点要用delete

---

一、移除链表中元素

203.移除链表元素

1、创建虚拟头结点用于记录
2、创建遍历节点用于遍历比较

ListNode* removeElements(ListNode* head, int val) {
	ListNode* dummy_head = new ListNode(0);//创建虚拟头结点
	dummy_head->next = head;//创建遍历节点
	ListNode* tarversal_head = dummy_head;
	while (tarversal_head->next != nullptr) {
		if (tarversal_head->next->val == val) {
			ListNode* temp = tarversal_head->next;
			tarversal_head->next = temp->next;
			delete temp;//空间回收
		}
		else {
			tarversal_head = tarversal_head->next;
		}
	}
	head = dummy_head->next;
	delete dummy_head;//空间回收
	return head;
}

82.删除排序链表中的重复元素II

方法一：递归

方法二：迭代

ListNode* deleteDuplicates(ListNode* head) {
    if (!head || !head->next) return head;
    ListNode dummyHead(0, head);
    ListNode* slow = &dummyHead;
    ListNode* fast = head;
    while (fast) {
        while (fast->next && fast->val == fast->next->val) fast = fast->next;
        if (slow->next != fast) slow->next = fast->next; //有重复元素，进行过移位操作
        else slow = slow->next;	//没有重复元素
        fast = fast->next;
    }
    return dummyHead.next;
}

19.删除链表的倒数第N个节点 【字节跳动+阿里】

左右节点指针，先拉远右节点指针，再进行左右并进直到找到倒数第N个节点，进行删除操作，注意左节点指针的next为待删除节点。

707.设计链表

二、反转链表元素

206.反转链表

双指针法：

ListNode* reverseList(ListNode* head) {
	ListNode* temp; // 保存cur的下一个节点
	ListNode* cur = head;
	ListNode* pre = NULL;
	while (cur) {
		temp = cur->next;  // 保存一下 cur的下一个节点，因为接下来要改变cur->next
		cur->next = pre; // 翻转操作
		// 更新pre 和 cur指针
		pre = cur;
		cur = temp;
	}
	return pre;
}

92.反转链表II 【字节跳动】

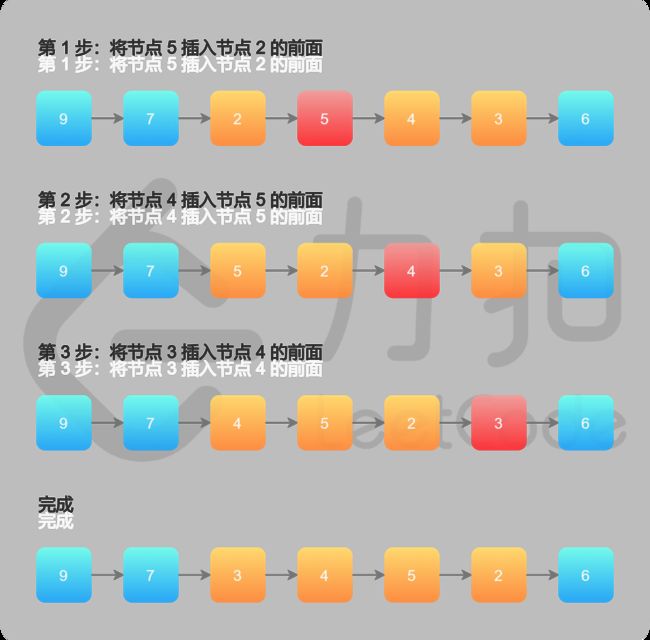
法一穿针引线：选定区域后反转，效率低

法二：一次遍历「穿针引线」反转链表（头插法）

ListNode* reverseBetween(ListNode* head, int left, int right) {
	ListNode* dummyNode = new ListNode(-1);
	dummyNode->next = head;
	ListNode* pre = dummyNode;
	for (int i = 0; i < left - 1; i++) {
		pre = pre->next;
	}
	ListNode* cur = pre->next;
	ListNode* next;
	for (int i = 0; i < right - left; i++) {
		next = cur->next;
		cur->next = next->next;
		next->next = pre->next;
		pre->next = next;
	}
	return dummyNode->next;
}

三、操作多链表

2.两数相加 【美团】

输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
    ListNode* head = new ListNode(-1); //head->next才是真正的头指针
    ListNode* curNode = head; //辅助指针
    int c = 0;//进位
    while (l1 || l2 || c) {
        int n1 = l1 ? l1->val : 0;
        int n2 = l2 ? l2->val : 0;
        ListNode* node = new ListNode((n1 + n2 + c) % 10);
        curNode->next = node; //链接下一个节点
        curNode = node; //更新当前节点
        l1 = l1 ? l1->next : nullptr;
        l2 = l2 ? l2->next : nullptr;
        c = (n1 + n2 + c) / 10;
    }
    return head->next;
}

21.合并两个有序链表 【快手】扩展考虑去重

同合并数组的双指针形式

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
    //创建新链表
    ListNode* dummyhead = new ListNode(-1);
    //创建遍历节点指针
    ListNode* head = dummyhead;
    //依次对两合并链表元素进行大小比较
    while (l1 != nullptr && l2 != nullptr) {
        if (l1->val < l2->val) {
            head->next = l1;
            l1 = l1->next;
        }
        else {
            head->next = l2;
            l2 = l2->next;
        }
        head = head->next;//添加完新元素之后，当前头结点向后推为新添加节点
    }
    head->next = l1 == nullptr ? l2 : l1; //对末尾剩余节点进行处理!!!
    return dummyhead->next;
}

23.合并K个升序链表 ★★★★★【字节跳动】优先级队列、分治

上题合并两个有序链表为基础
方法一：归并排序

class Solution {
public:
    //合并两链表
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        //创建新链表
        ListNode* preHead  = new ListNode(-1);
        ListNode* head = preHead;
        //依次对两合并链表元素进行大小比较
        while(l1!=nullptr && l2 !=nullptr){
            if(l1->val<l2->val){
                head->next = l1;
                l1 = l1->next;
            }
            else{
                head->next = l2;
                l2 = l2->next;
            }
            head=head->next;//添加完新元素之后，当前头结点向后推为新添加节点
        }
        head->next = l1==nullptr?l2:l1;
        return preHead->next;
    }
    //递归，将lists数组进行分化
    ListNode* merge(vector<ListNode*> &lists , int left , int right){
        //终止条件
        if(left==right) return lists[left];
        int mid = (left+right)>>1;
        return mergeTwoLists( merge(lists,left,mid) , merge(lists , mid+1 ,right) );
    }

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        //方法一：归并排序
        if(lists.size()==0) return nullptr;
        return merge(lists,0,lists.size()-1);
    }
};

方法二：优先级队列
维护当前每个链表没有被合并的元素的最前面一个，k 个链表就最多有 k 个满足这样条件的元素，每次在这些元素里面选取 val 属性最小的元素合并到答案中。在选取最小元素的时候，我们可以用优先队列来优化这个过程。

class Solution {
public:
    //自定义结构体中使用仿函数operator<
    struct Status{
        int val;
        ListNode* pre;
        bool operator<(const Status &cur)const{
            return val>cur.val;//导致小顶堆
        }
    };
    
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        //方法一：归并排序
        if(lists.size()==0) return nullptr;
        priority_queue<Status> que; //创建小顶堆进行堆排序
        for(auto node:lists){
            if(node) que.push({node->val,node}); //依次插入生成小顶堆
        }
        ListNode* dummyhead=new ListNode(0);//虚拟头结点
        ListNode* head = dummyhead;//遍历节点
        while(!que.empty()){
            //将最小值出队列
            auto node = que.top();
            que.pop();
            //记录当前出队节点
            head->next = node.pre;
            head = head->next;//依次递推
            if(node.pre->next!=nullptr){
                que.push({node.pre->next->val,node.pre->next});
            }
        }
        return dummyhead->next;
    }
};

24.两两交换链表中的节点

法一：双指针

法二：递归：

ListNode* swapPairs(ListNode* head) {
	if (head == nullptr || head->next == nullptr) {
		return head;
	}
	ListNode* newHead = head->next;
	head->next = swapPairs(newHead->next);
	newHead->next = head;
	return newHead;
}

面试题02.07.链表相交

160.相交链表

• 指针 A 先遍历完链表 headA ，再开始遍历链表 headB ，当走到 node 时，共走步数为：
  $a+(b-c)$
• 指针 B 先遍历完链表 headB ，再开始遍历链表 headA ，当走到 node 时，共走步数为：
  $b+(a-c)$

ListNode* getIntersectionNode(ListNode* headA, ListNode* headB) {
    if (headA == nullptr || headB == nullptr) {
        return nullptr;
    }
    ListNode* pA = headA, * pB = headB;
    while (pA != pB) {
        pA = pA == nullptr ? headB : pA->next;
        pB = pB == nullptr ? headA : pB->next;
    }
    return pA;
}

四、环形链表

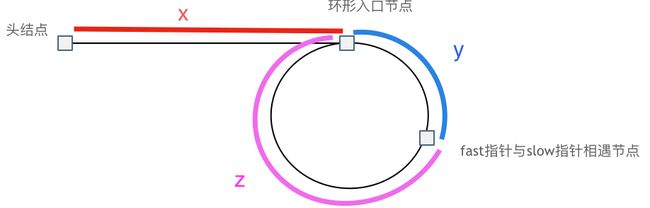
检验环形链表是否存在，使用快慢指针，快慢指针同时移动，慢指针移动一格，快指针移动两格。
关于移动距离（节点数）：
slow：$x+y$
fast：$x+y+n(y+z),n>=1$
slow的路径距离为fast的路径距离的一半：$2\ast (x+y)=x+y+n(y+z)->x=(n-1)(y+z)+z$
当取第一次相遇即n=1时，$x=z$

141.环形链表

142.环形链表II

ListNode* detectCycle(ListNode* head) {
	ListNode* fast = head;
	ListNode* slow = head;
	while (fast != nullptr && fast->next != nullptr) {
		slow = slow->next;
		fast = fast->next->next;
		if (slow == fast)
		{
			ListNode* index1 = fast;
			ListNode* index2 = head;
			while (index1 != index2) {
				index2 = index2->next;
				index1 = index1->next;
			}
			return index2;
		}
	}
	return nullptr;
}

25.K个一组翻转链表

五、排序

最适合链表的排序算法是归并排序

143.重排链表 【字节跳动+美团】

给定一个单链表 L 的头节点 head ，单链表 L 表示为：
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为：
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …

方法：寻找链表中点 + 链表逆序 + 合并链表
注意到目标链表即为将原链表的左半端和反转后的右半端合并后的结果。

这样我们的任务即可划分为三步：

1. 找到原链表的中点（参考「876. 链表的中间结点」）。
   我们可以使用快慢指针来 O(N)O(N) 地找到链表的中间节点。
2. 将原链表的右半端反转（参考「206. 反转链表」）。
   我们可以使用迭代法实现链表的反转。
3. 将原链表的两端合并。
   因为两链表长度相差不超过 11，因此直接合并即可。

147.对链表进行插入排序

插入排序的时间复杂度是 $O(n^2)$，其中 n 是链表的长度。

148.排序链表 ★★★★★【字节跳动国际化电商】

最适合链表的排序算法是归并排序，归并排序的时间复杂度$O(nlogn)$ 空间复杂度 $O(1)$。
方法一：自顶向下 时间复杂度$O(nlogn)$ 空间复杂度 $O(n)$

1. 通过快慢指针找到链表中点进行左右链表分割
2. 对分割后的左右链表进行递归分割
3. 对递归分割后的小链表进行合并（有序链表合并）

class sortList02 {
public:
    ListNode* sortList(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        //
        ListNode* fast = head;
        ListNode* slow = head;
        ListNode* brk;
        while (fast != nullptr && fast->next != nullptr) {
            fast = fast->next->next;
            if (fast == nullptr || fast->next == nullptr) {
                brk = slow;//找到中间链表节点
            }
            slow = slow->next;
        }
        brk->next = nullptr;
        //对左右两链表进行递归
        ListNode* head1 = sortList(head);
        ListNode* head2 = sortList(slow);
        //对左右两链表进行合并(合并有序链表)
        ListNode* dummyhead = new ListNode(0), * cur = dummyhead;
        while (head1 != nullptr && head2 != nullptr) {
            if (head1->val < head2->val) {
                cur->next = head1;
                cur = cur->next;
                head1 = head1->next;
            }
            else {
                cur->next = head2;
                cur = cur->next;
                head2 = head2->next;
            }
        }
        cur->next = head1 == nullptr ? head2 : head1;
        return dummyhead->next;
    }
};

方法二：自底向上 时间复杂度$O(nlogn)$ 空间复杂度 $O(1)$

class Solution {
public:
    ListNode* sortList(ListNode* head) {
        if (head == nullptr) {
            return head;
        }
        int length = 0;
        //记录链表长度
        ListNode* node = head;
        while (node != nullptr) {
            length++;
            node = node->next;
        }
        ListNode* dummyHead = new ListNode(0, head);
        //依次
        for (int subLength = 1; subLength < length; subLength <<= 1) {
            ListNode* prev = dummyHead, *curr = dummyHead->next;
            while (curr != nullptr) {
            	//有序链表head1
                ListNode* head1 = curr;
                for (int i = 1; i < subLength && curr->next != nullptr; i++) {
                    curr = curr->next;
                }
                //有序链表head2
                ListNode* head2 = curr->next;
                curr->next = nullptr;
                curr = head2;
                for (int i = 1; i < subLength && curr != nullptr && curr->next != nullptr; i++) {
                    curr = curr->next;
                }
                ListNode* next = nullptr;
                if (curr != nullptr) {
                    next = curr->next;
                    curr->next = nullptr;
                }
                //合并两有序链表head1 head2
                ListNode* merged = merge(head1, head2);
                
                prev->next = merged;
                while (prev->next != nullptr) {
                    prev = prev->next;
                }
                curr = next;
            }
        }
        return dummyHead->next;
    }
	//合并有序链表
    ListNode* merge(ListNode* head1, ListNode* head2) {
        ListNode* dummyHead = new ListNode(0);
        ListNode* cur= dummyHead;
        while (head1!= nullptr && head2!= nullptr) {
            if (head1->val <= head2->val) {
                cur->next = head1;
                head1= head1->next;
            } else {
                cur->next = head2;
                head2= head2->next;
            }
            cur= cur->next;
        }
        cur->next = head1==nullptr?head2:head1;
        return dummyHead->next;
    }
};

六、双向链表

146.LRU缓存★★★★★ 【字节+阿里】

struct DListNode {
	int key, value;
	DListNode* prev;
	DListNode* next;
	DListNode() :key(0), value(0), prev(nullptr), next(nullptr) {}
	DListNode(int _key, int _value) :key(_key), value(_value), prev(nullptr), next(nullptr) {}
};

class LRUCache {
private:
	//创建哈希表用于get函数快速查找key值对应的双向链表节点
	unordered_map<int, DListNode*>cache;
	DListNode* head;
	DListNode* tail;
	int size;//当前双向链表节点数量
	int capacity;//双向链表节点容量

	void addToHead(DListNode* node){
		head->next->prev = node;
		node->next = head->next;
		node->prev = head;
		head->next = node;
	}

	void removeNode(DListNode*node) {
		node->prev->next = node->next;
		node->next->prev = node->prev;
	}
	//将链表中的节点node放置头部
	void moveToHead(DListNode* node) {
		removeNode(node);
		addToHead(node);
	}

	//删除并返回最后一个节点
	DListNode* removeTail() {
		DListNode* node = tail->prev;
		removeNode(node);
		return node;
	}

public:
	LRUCache(int _capacity) :capacity(_capacity), size(0) {
		head = new DListNode();
		tail = new DListNode();
		head->next = tail;
		tail->prev = head;
	}

	int get(int key) {
		//判断key是否存在
		if (!cache.count(key)) {
			return -1;
		}
		else {
			DListNode* temp = cache[key];
			//访问后将DListNode节点放到链表首部
			moveToHead(temp);
			return temp->value;
		}
	}

	//插入
	void put(int key, int value) {
		if (!cache.count(key)) {
			//key未找到，创建该节点
			DListNode* node = new DListNode(key,value);
			//添加到哈希表
			cache[key] = node;
			//将节点添加到双向链表
			addToHead(node);
			//判断链表是否超出
			++size;
			if (size > capacity) {
				//移除双向链表的最后的节点
				DListNode* removeNode = removeTail();
				//删除哈希表中节点
				cache.erase(removeNode->key);
				delete removeNode;
				--size;
			}
		}
		else {
			//找到key
			//通过哈希表定位
			DListNode* node = cache[key];
			//修改双向链表中的value并调整位置
			node->value = value;
			moveToHead(node);
		}
	}
};

字节：定时过期的 LRU 算法

添加关于时间的头文件time.h

struct DListedNode {
	int key, value;
	time_t expireTime;
	DListedNode* prev,* next;
	DListedNode() :key(0), value(0), expireTime(ttl),prev(nullptr), next(nullptr) {}
	DListedNode(int _key, int _value,int _expireTime) :key(_key), value(_value),
		expireTime(_expireTime), prev(nullptr), next(nullptr) {}
};


class LRUCache {
private:
	//创建哈希表用于get函数快速查找key值对应的双向链表节点
	unordered_map<int, DListedNode*>cache;
	DListedNode* head;
	DListedNode* tail;
	int size;//当前双向链表节点数量
	int capacity;//双向链表节点容量

	void addToHead(DListedNode* node){
		//修改节点的时间
		//每次重新插入均重置超时时间为 curTime + ttl
		time_t curTime = time(nullptr);
		DListedNode* temp = new DListedNode(node->key, node->value, curTime + ttl);
		delete node;//删除旧节点，新节点替代
		head->next->prev = temp;
		temp->next = head->next;
		temp->prev = head;
		head->next = temp;
	}
	void removeNode(DListedNode*node) {
		node->prev->next = node->next;
		node->next->prev = node->prev;
	}
	//将链表中的节点node放置头部
	void moveToHead(DListedNode* node) {
		removeNode(node);
		addToHead(node);
	}
	//删除并返回最后一个节点
	DListedNode* removeTail() {
		DListedNode* node = tail->prev;
		removeNode(node);
		return node;
	}
public:
	LRUCache(int _capacity) :capacity(_capacity), size(0) {
		head = new DListedNode();
		tail = new DListedNode();
		head->next = tail;
		tail->prev = head;
	}

	int get(int key) {
		//判断key是否存在
		if (!cache.count(key)) {
			return -1;
		}
		else {
			DListedNode* temp = cache[key];
			//在访问时就判断该数据是否过期
			//采用 time.h 头文件中的 time 函数获取系统当前时间
			time_t curTime = time(nullptr);
			//判断是否过期,利用 difftime 函数比较节点过期时间与系统当前时间的大小
			if (difftime(temp->expireTime, curTime) <= 0) {
				//过期
				removeNode(temp);
				cache.erase(temp->key);
				delete temp;
				--size;
				return -1;
			}
			else {
				//访问后将DListNode节点放到链表首部
				moveToHead(temp);
				return temp->value;
			}
		}
	}

	//插入
	void put(int key, int value) {
		if (!cache.count(key)) {
			//key未找到，创建该节点
			DListedNode* node = new DListedNode(key,value,ttl);
			//添加到哈希表
			cache[key] = node;
			//将节点添加到双向链表
			addToHead(node);
			//判断链表是否超出
			++size;
			if (size > capacity) {
				//先查看是否存在过期节点
				time_t curTime = time(nullptr);
				bool isExpire = false;//标记是否有过期节点
				//遍历hash表试图寻找第一个过期的节点
				unordered_map<int,DListedNode*>::iterator it;
				for (it = cache.begin(); it != cache.end(); it++) {
					if (difftime(it->second->expireTime, curTime) <= 0)
					{
						isExpire = true;
						break;
					}
				}
				if (isExpire) {
					//有过期节点，淘汰过期节点
					removeNode(it->second);
					cache.erase(it->second->key);
					delete it->second;
					--size;
				}
				else {
					//移除双向链表的最后的节点
					DListedNode* removeNode = removeTail();
					//删除哈希表中节点
					cache.erase(removeNode->key);
					delete removeNode;
					--size;
				}
			}
		}
		else {
			//找到key
			//通过哈希表定位
			DListedNode* node = cache[key];
			//修改双向链表中的value并调整位置
			node->value = value;
			moveToHead(node);
		}
	}
};

---

总结

参考博客：
代码随想录
力扣HOT100
力扣剑指offer
CodeTop