刷题记录Day15-二叉树(层序遍历、翻转二叉树、对称二叉树)
刷题记录Day15-二叉树(层序遍历、翻转二叉树、对称二叉树)
文章目录
- 刷题记录Day15-二叉树(层序遍历、翻转二叉树、对称二叉树)
- 前言
- 一、二叉树的层序遍历
-
- 1. 102二叉树的层序遍历
- 2. 107二叉树的层序遍历II
- 3. 199二叉树的右视图
- 4. 637二叉树的层平均值
- 5. 429N叉树的层序遍历
- 6. 515在每个树行中找最大值
- 7. 116填充每个节点的下一个右侧节点指针
- 8. 117填充每个节点的下一个右侧节点指针II
- 9. 104二叉树的最大深度
- 10. 111二叉树的最小深度
- 二、翻转二叉树
-
- 1. 226翻转二叉树
- 三、 对称二叉树
-
- 1. 101对称二叉树
- 总结
前言
题目来源:leetcode
刷题顺序:代码随想录
刷题工具:VSCode+leetcode插件
补充:延毕时间充裕,会结合LeetCode 101: A LeetCode Grinding Guide (C++ Version)相似题目一起做。
一、二叉树的层序遍历
1. 102二叉树的层序遍历
题目:
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
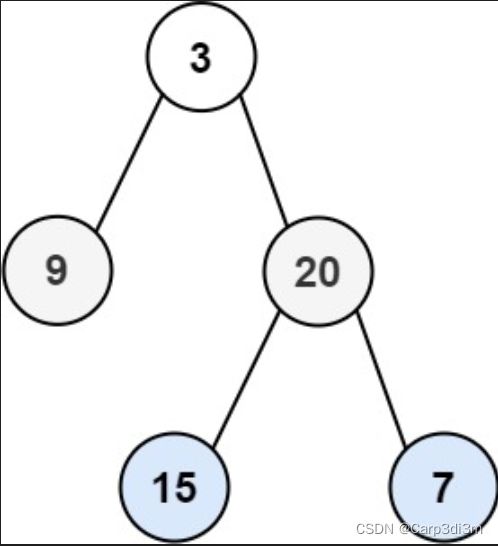
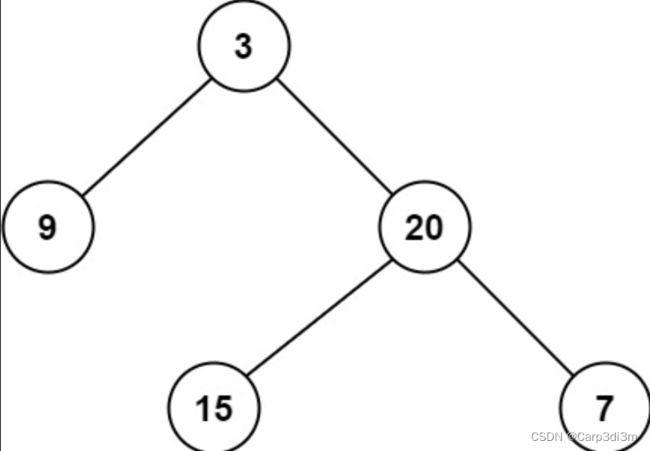
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
代码:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
vector<vector<int>> res;
if (root != NULL) que.push(root);
while (!que.empty()){
vector<int> vec;
int size = que.size();
while (size--){
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
res.push_back(vec);
}
return res;
}
};
2. 107二叉树的层序遍历II
题目:
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
输入:root = [3,9,20,null,null,15,7]
输出:[[15,7],[9,20],[3]]
代码:
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
queue<TreeNode*> que;
vector<vector<int>> res;
if (root != NULL) que.push(root);
while (!que.empty()){
int size = que.size();
vector<int> vec;
while (size--){
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
res.push_back(vec);
}
reverse(res.begin(),res.end());
return res;
}
};
就把层序遍历的二维数组reverse一下。
3. 199二叉树的右视图
题目:
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
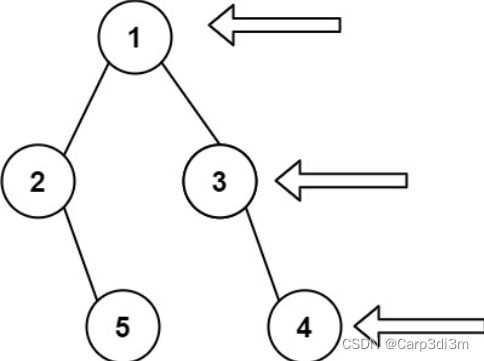
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]
代码:
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<int> res;
queue<TreeNode*> que;
if (root != NULL) que.push(root);
while (!que.empty()){
int size = que.size();
while (size--){
TreeNode* node = que.front();
que.pop();
if (size == 0) res.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return res;
}
};
4. 637二叉树的层平均值
题目:
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10^-5 以内的答案可以被接受。
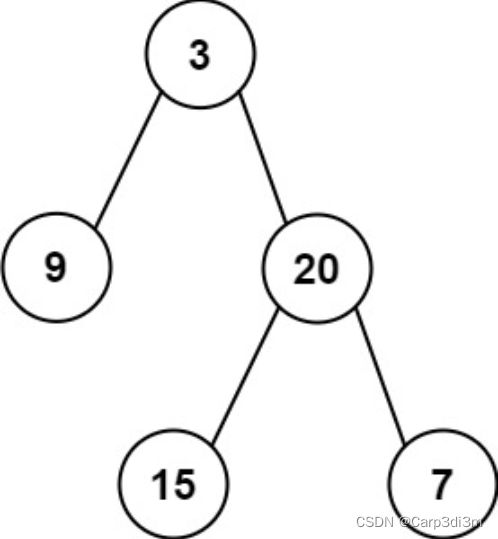
输入:root = [3,9,20,null,null,15,7]
输出:[3.00000,14.50000,11.00000]
解释:第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。
代码:
class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
vector<double> res;
queue<TreeNode*> que;
if (root != NULL) que.push(root);
while (!que.empty()){
int size = que.size();
double num = que.size();
double sum = 0;
while (size--){
TreeNode* node = que.front();
que.pop();
sum += (double)node->val;
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
res.push_back(sum/num);
}
return res;
}
};
5. 429N叉树的层序遍历
题目:
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
示例:
输入:root = [1,null,3,2,4,null,5,6]
输出:[[1],[3,2,4],[5,6]]
代码:
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
vector<vector<int>> res;
queue<Node*> que;
if (root != NULL) que.push(root);
while (!que.empty()){
int size = que.size();
vector<int> vec;
while (size--){
Node* node = que.front();
que.pop();
vec.push_back(node->val);
if (!node->children.empty()){
for (int i =0; i <node->children.size(); ++i){
que.push(node->children[i]);
}
}
}
res.push_back(vec);
}
return res;
}
};
6. 515在每个树行中找最大值
题目:
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]
代码:
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
vector<int> res;
queue<TreeNode*> que;
if (root != NULL) que.push(root);
while(!que.empty()){
int size = que.size();
int tmp = INT_MIN;
while (size--){
TreeNode* node = que.front();
que.pop();
tmp = max(node->val, tmp);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
res.push_back(tmp);
}
return res;
}
};
7. 116填充每个节点的下一个右侧节点指针
题目:
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
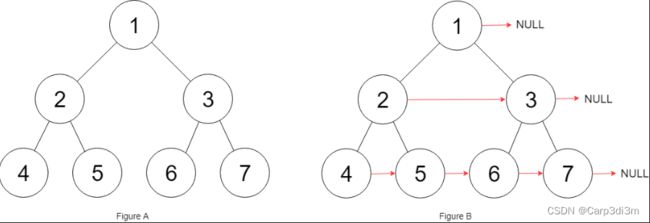
输入:root = [1,2,3,4,5,6,7]
输出:[1,#,2,3,#,4,5,6,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
代码:
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if (root != NULL) que.push(root);
while(!que.empty()){
int size = que.size();
while (size--){
Node* node = que.front();
que.pop();
if (size>0){
node->next = que.front();
}
else{
node->next = NULL;
}
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return root;
}
};
8. 117填充每个节点的下一个右侧节点指针II
题目:
给定一个二叉树:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL 。
初始状态下,所有 next 指针都被设置为 NULL 。
示例:
输入:root = [1,2,3,4,5,null,7]
输出:[1,#,2,3,#,4,5,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),'#' 表示每层的末尾。
代码:
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if (root != NULL) que.push(root);
while (!que.empty()){
int size = que.size();
while (size--){
Node* cur = que.front();
que.pop();
if (size >0){
cur->next = que.front();
}
else{
cur->next = NULL;
}
if (cur->left) que.push(cur->left);
if (cur->right) que.push(cur->right);
}
}
return root;
}
};
跟116题一样
9. 104二叉树的最大深度
题目:
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例:
输入:root = [3,9,20,null,null,15,7]
输出:3
代码:
class Solution {
public:
int maxDepth(TreeNode* root) {
int res = 0;
queue<TreeNode*> que;
if (root != NULL) que.push(root);
while (!que.empty()){
int size = que.size();
while (size--){
TreeNode* node = que.front();
que.pop();
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
++res;
}
return res;
}
};
10. 111二叉树的最小深度
题目:
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例:
输入:root = [3,9,20,null,null,15,7]
输出:2
代码:
class Solution {
public:
int minDepth(TreeNode* root) {
int res = 0;
queue<TreeNode*> que;
if (root != NULL) que.push(root);
while (!que.empty()){
int size = que.size();
++res;
while (size--){
TreeNode* node = que.front();
que.pop();
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
if (!node->left && !node->right){
return res;
}
}
}
return res;
}
};
二、翻转二叉树
1. 226翻转二叉树
题目:
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
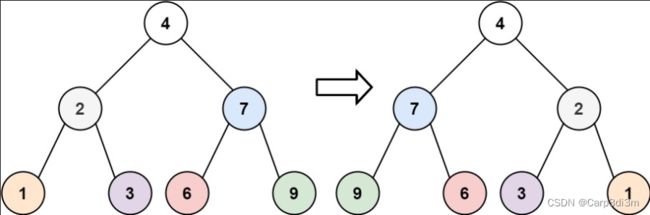
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
代码:
方法一,前序递归法
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (root == NULL) return root;
swap(root->left,root->right); //中
invertTree(root->left); //左
invertTree(root->right); //右
return root;
}
};
方法二,深度优先遍历(前序迭代法)
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()){
TreeNode* node = st.top();
st.pop();
swap(node->left,node->right); //中
if (node->right) st.push(node->right); //左
if (node->left) st.push(node->left); //右
}
return root;
}
};
方法三,广度优先遍历
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
while (!que.empty()){
int size = que.size();
while (size--){
TreeNode* node = que.front();
que.pop();
swap(node->left,node->right);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return root;
}
};
三、 对称二叉树
1. 101对称二叉树
题目:
给你一个二叉树的根节点 root , 检查它是否轴对称。
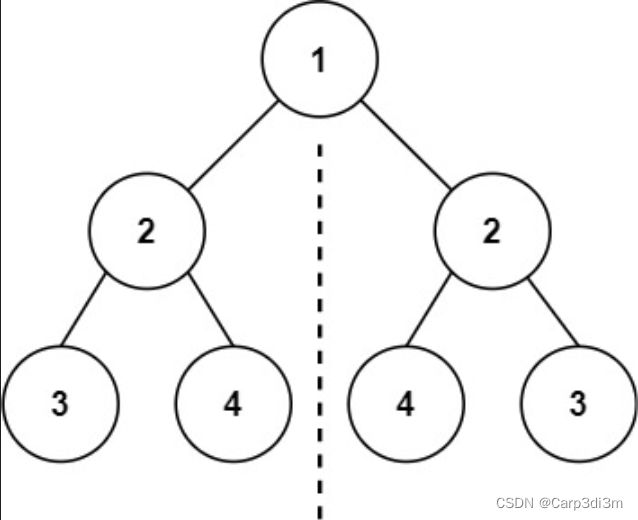
输入:root = [1,2,2,3,4,4,3]
输出:true
代码:
class Solution {
public:
bool compare(TreeNode* node1, TreeNode* node2){
if (node1 ==NULL && node2 !=NULL) return false;
else if (node1 !=NULL && node2 ==NULL) return false;
else if (node1 ==NULL && node2 ==NULL) return true;
else if (node1->val != node2->val) return false;
bool rule1 = compare(node1->left, node2->right);
bool rule2 = compare(node1->right, node2->left);
bool isSame = rule1 && rule2;
return isSame;
}
bool isSymmetric(TreeNode* root) {
return compare(root->left,root->right);
}
};
虽然我没写出来,但是思路和卡哥讲的是一样的,都是用递归,代码几乎一样但是没有考虑好空指针。
我没有过多思考遍历顺序的问题。
我认为这道题对称关键在于:两个节点从根节点出发(node1,node2)。node1如果向左,那么node2向右的值就得与其相等;如果node1向右,那么node2向左的值就与其相等。即我们要同时判断node1->left == node2->right和node1->right == node2->left。如果两者皆满足,那这就是一个对称的二叉树。
总结
层序遍历都是套模板的题目,虽然ac的很爽,但是还是要加强记忆。
二叉树里的递归好烦,我感觉我懂什么意思,但实现的时候又感觉有很多小问题注意不到。