基础矩阵

一 实验背景

问题引入：用两个相机在不同的位置拍摄同一物体，如果两张照片中的景物有重叠的部分，就可以说这两张照片之间存在一定的对应关系。本次实验的任务就是描述它们之间的对应关系，描述工具是对极几何。

1.对极几何

1.1基本概念
对极几何是图像平面与以基线为轴的平面束的交的几何（这里的基线是指连接摄像机中心的直线）。
以下图为例：

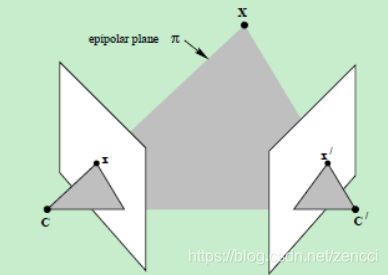
对极几何描述的是左右两幅图像（点x和x’对应的图像）与以CC’为轴的平面束的交的几何。

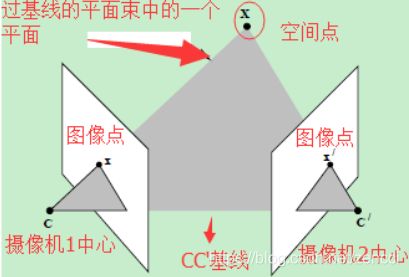
直线CC’为基线，以该基线为轴存在一个平面束，该平面束与两幅图像平面相交。
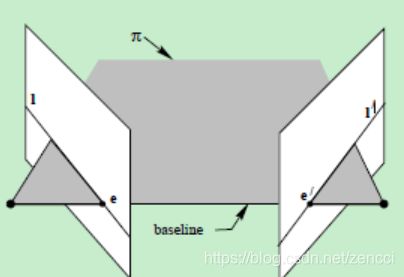
下图为该平面束的直观形象，可以看到，该平面束中不同平面与两幅图像相交于不同直线：

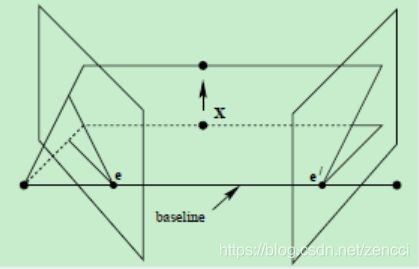
过e, e′的平面 π ,其平面上所有点在两个像平面中的 投影分别为直线 l 与 l’。
上图中的平面π，只是过基线的平面束中的一个平面。上述平面π 的集与像平面的交线集，分别相交于e与e’。

1.2对极几何的一个重要约束—5点共面约束
下图中，空间点X在两幅图像中的像分别为x和x’，这两个投影点之间是否存在某种关系？

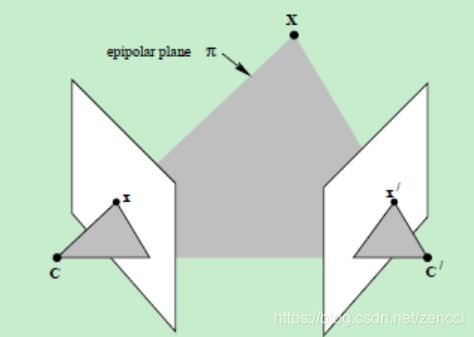
点x、x’与摄像机中心C和C’是共面的，并且与空间点X也是空面的，这5个点共面于平面π。这是一个最本质的约束，即5个点决定了一个平面π。
由上述约束，可以推导出一个重要性质：由图像点x和x’反投影的射线共面。

1.3对极几何的相关概念

①对极点：基线与像平面交点（光心在另一幅图像中的投影），如上图中的点e和e’。
②对极平面：包含基线的平面，如上图中的π。
③对极线：对极平面与像平面的交线，如上图中的直线l和l’。
④对极平面束：以基线为轴的平面束，上图给出了包含两个平面的对极平面束。

1.4对应点的约束
假设现在只知道图像点x，那么如何约束它的对应点x’呢？

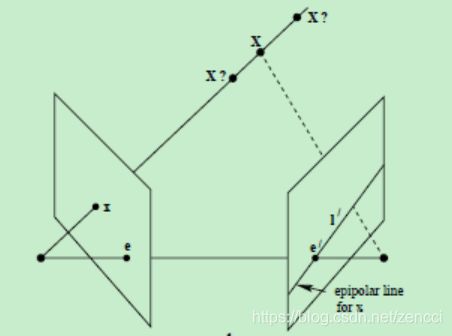
由于点x和x’一定位于平面π上，而平面π可以利用基线CC’和图像点x的反投影射线确定。点x’又是右侧图像平面上的点，所以，点x’一定位于平面π与右侧图像平面的交线l’上。且直线l’为点x的对极线，也就是说，点x的对应点x’一定位于它的对极线上。

2.基础矩阵

2.1
基础矩阵是对极几何的代数表达方式。
若已知基础矩阵F，和一个3D点在一个像平面上的像素坐标p，通过基础矩阵可以求得在另一个像面上的像素坐标p’。

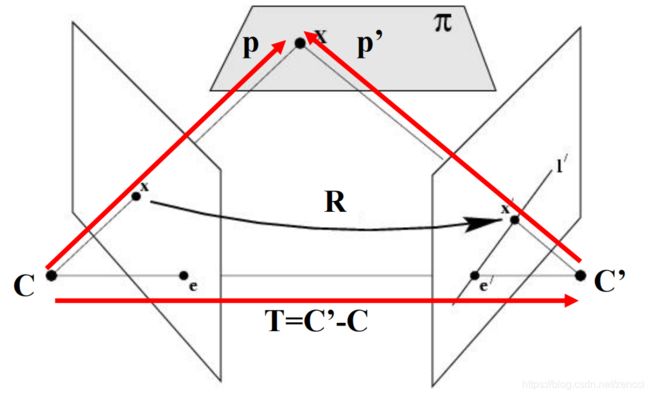
以C为原点，光轴方向为z轴，另外两个方向为x, y轴可以得到一个坐标系，在这个坐标系下，可以对x，p，x’得到三维坐标。同理，对C’也可以得到一个三维坐标，这两个坐标之间的转换矩阵为[R T]，即通过旋转Ｒ和平移Ｔ可以将C坐标系下的点X(x1, y1, z1)， 转换成C’坐标系下的X’(x2, y2, z2)。
则有 p=Rp’+T
设x=Kp,x’=Kp’，则根据三点共面可以得到：


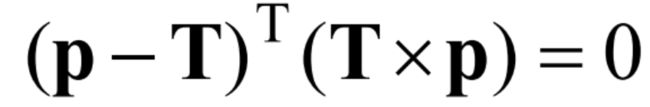
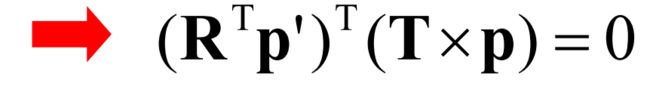
其中，p, p’分别为X点的像点在两个坐标系下分别得到的坐标。Rp’为极面上一矢量，T为极面上一矢量，两个矢量叉乘为极面的法向量， 且这个法向量与极面上一矢量X一定是垂直的。
叉积又可以写成矩阵相乘的形式，所以

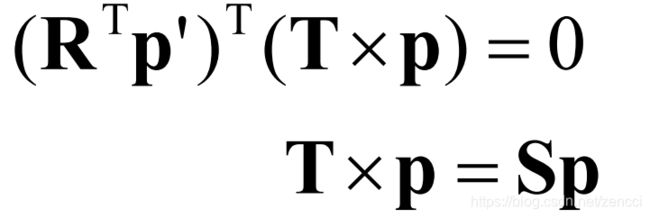
定义矩阵S为S矩阵的秩为2，即T和P的叉积的秩为2。
将上式带入叉积公式中，得到：

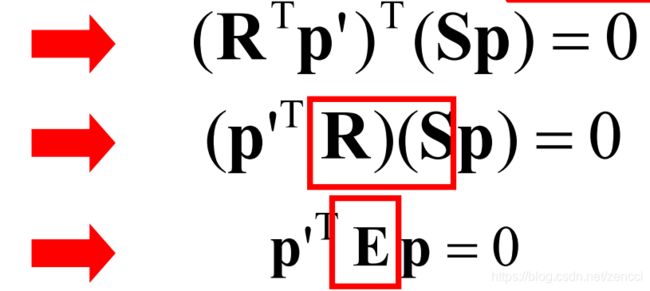
这里的E为本质矩阵，它包含了物理空间中两个摄像机相关的旋转（R）和平移信息（T）。
本质矩阵描述了空间中的点在两个坐标系中的坐标对应关系。

上式中， K和K’为相机的校准矩阵， 描述相机的内参数， p和p’为相机的像素坐标。将上式代入
得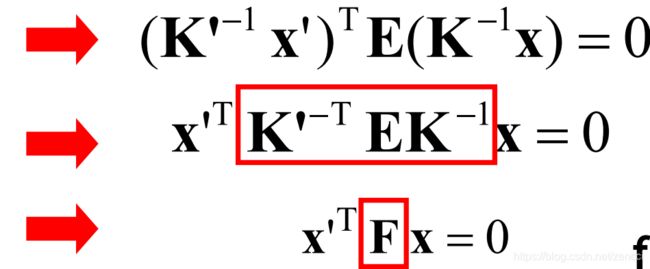：这里的F即为基础矩阵，除了包含E的信息外，还包含了两个摄像机的内参数。
基础矩阵描述了空间中的点在两个像平面中的坐标对应关系。
基础矩阵描述了图像中任意对应点 x↔x’ 之间的约束关系。
这样我们就得到了两个相机上的像素坐标和基础矩阵F之间的关系了。

2.2基础矩阵的性质：
①F为3x3 矩阵，秩为2，对任意匹配点对 x↔x’ 均满足 xTFx’=0；
②转置: 如果F是表述点对 (x, x’)之间的基础矩阵, 则 FT是 表述点对 (x’,x)之间的基础矩阵；
③对极线: F 可以将点 x 映射到对应像平面上一条线 l=Fx ，同理可得 l’=FTx；
④对极点: 对于所有对极线, 有 eTFx’=0, 同理∀x’ =>eT=0，有 Fe’=0；
⑤F的自由度为7（一般情况下，3*3的矩阵自由度为9，但是因为相差一个常数因子和行列式值为0两个条件，减掉2个自由度）
2.3基础矩阵的用途：
①简化匹配
②去除错配特征
2.4
①极点位于像平面

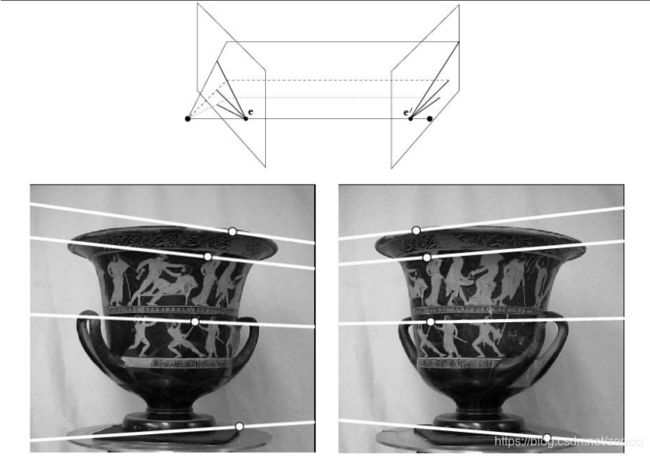
如图，两个相机相对放置， 相机1面向右边，相机2面向左边，可知极点位于1的右边，2的左边。图中花瓶上标示的横线即为平行于基线的线条。
上图中，平行于基线的线条所在极面与像平面必交于极点（基线必与像面交于极点），所以这些线条在像面上一定会交于极点。

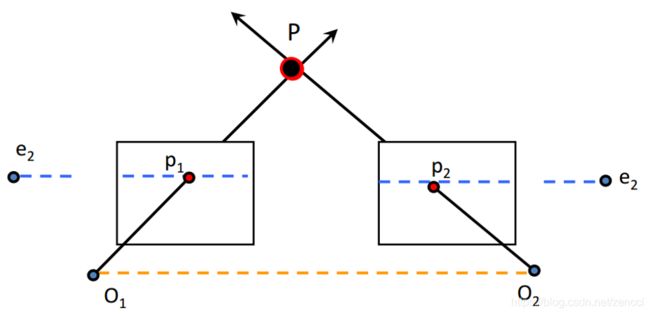
②基线平行像平面

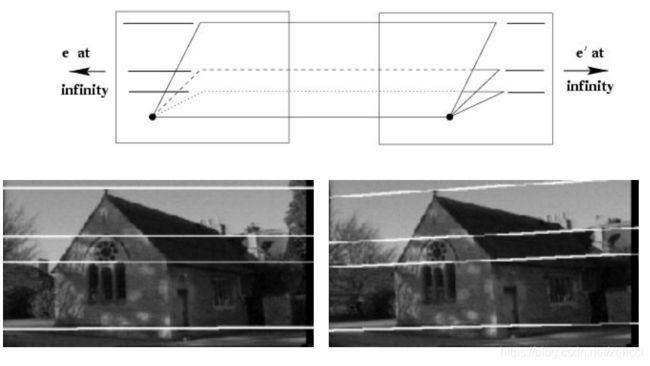
根据极点的定义，则极点位于无穷远处，极线与基线平行，如上图，这个时候，与基线平行的线条的在像面是一系列平行线，消失点在无穷远，和极点重合。
③相机前后方位关系


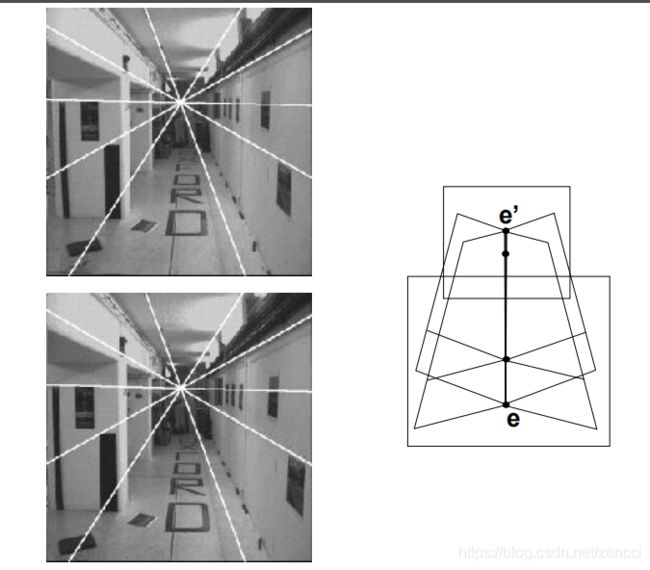
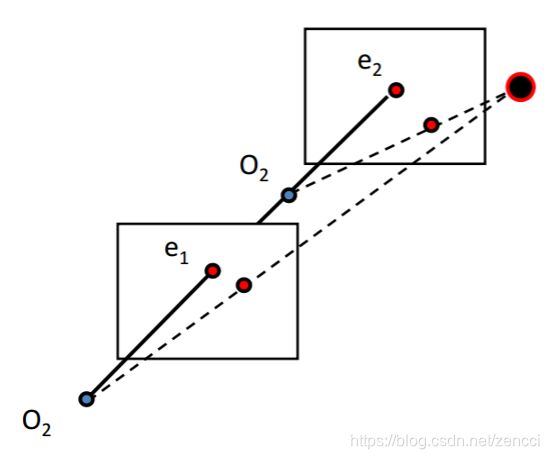
两个相机是前后放置且主点连线和像面垂直时，极点在各自像平面上的位置相同，且平行基线的线条在像面上的位置如上图右边所示，同样消失点为极点。

2.5 8点估算法
因为基础矩阵有7个自由度，所以确定基础矩阵最简单的方法就是8点算法。
由于基础矩阵F定义为：

任给两幅图像中的匹配点 x 与 x’ 。 令 x=任给两幅图像中的匹配点 x 与 x’ 。
令 x=(u,v,1)T ，x’=(u’,v’,1)T

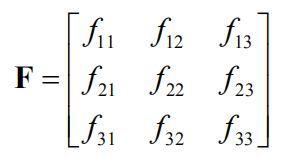
把基础矩阵F的各个元素当作一个向量处理，则有相应方程：


在实际计算中，可以直接用ATA的分解来求解参数。 也可以用非线性优化，通过搜索f使得||Af||最小化, 同时满足||f||=1的约束。
上述求解后的F不一定能满足秩为2的约束，因此还要在F基础上加以约束。
通过SVD分解可以解决上述问题，令 S=UƩVT则

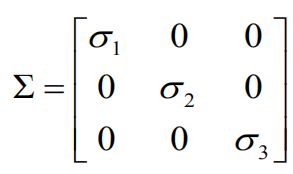
令

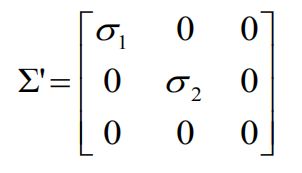
则最终的解为

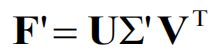
8点法的优点是线性求解，容易实现，运行速度快；缺点是对噪声敏感。
由于矩阵各列的数据尺度差异太大， 最小二乘得到的结果精度一般很低，所以采用归一化8点算法。

2.6归一化8点算法
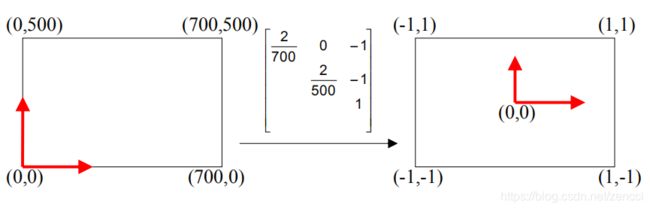
1.将图像坐标变换到合适的范围 ^Xi,=TXi ，^Xi’,=TXi’
2.根据变换后的坐标^Xi ，^Xi’ 计算归一化举出矩阵^F
3.还原原始基础矩阵 F=T’TF^T

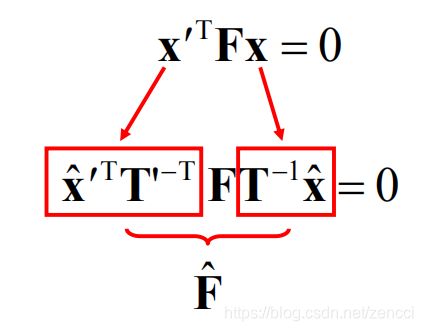
归一化8点算法将图像坐标范围限定在 ~[-1,1]x[1,1]
实验表明可以得到更可靠的结果。

二 实验内容

1.实验图片

（1）场景1：左右拍摄，极点位于图像平面上

（2）场景2：像平面接近平行，极点位于无穷远

（3）场景3：图像拍摄位置位于前后

2.实验结果

（1）场景1：



基础矩阵：

极点极线：