冒泡排序和快速排序（分治递归算法）

冒泡排序：

冒泡排序时间复杂度为O（N^2）

直接插入排序比冒泡排序适应性更好，数据接近有序时比直接选择排序更好。

冒泡排序代码：

void PrintArray(int* a, int n)
{
	int i;
	for (i = 0; i < n; i++)
	{
		printf("%d ", *(a + i));
	}
}
void Swap(int* a, int* b)
{
	int tem = *a;
	*a = *b;
	*b = tem;
}
void BubbleSort(int* a, int n)
{
	int i,j;
	for (i = 0; i < n; i++)
	{
		for (j = 0; j < n - i - 1; j++)
		{
			if (a[j] < a[j + 1])
			{
				Swap(&a[j], &a[j + 1]);
			}
		}
	}
}
void TestBubbleSort()
{
	int a[] = { 3,5,2,7,8,6,1,9,4,0 };
	BubbleSort(a, sizeof(a) / sizeof(int));
	PrintArray(a, sizeof(a) / sizeof(int));
}

快速排序：

1.挖坑法

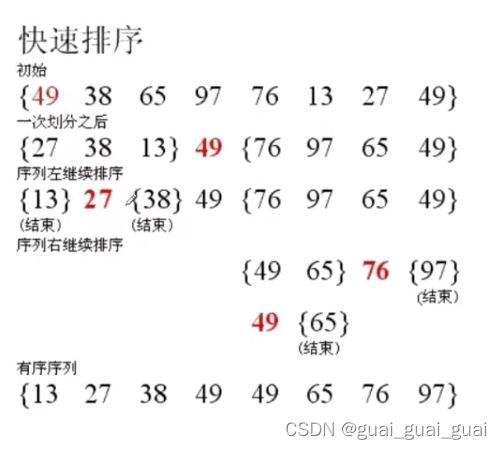
以下为快速排序的一次遍历，即将key放至排序好之后的位置，pivot为坑

之后利用分治递归对6左右两边分别进行一次排序 ，原理如下图：

//快速排序(1.挖坑法)
void QuickSort1(int* a, int left,int right)
{
	if (left >= right)
		return;
	int begin = left, end = right;
	int pivot = begin;
	int key = a[begin];
	while (begin < end)
	{
		//右边找小，放到左边
		while (begin < end &&a[end] >= key)
		{
			end--;
		}
		//小的放在左边的坑里，自己形成一个新的坑
		a[pivot] = a[end];
		pivot = end;
		//左边找大，放到右边
		while (begin < end &&a[begin] <= key)
		{
			begin++;
		}
		//大的放在右边的坑里，自己形成一个新的坑
		a[pivot] = a[begin];
		pivot = begin;
	}
	pivot = begin;
	a[pivot] = key;
	//[left,pivot-1]pivot[pivot+1,right] 分治递归
	QuickSort(a, left, pivot - 1);
	QuickSort(a, pivot + 1, right);
}
void TestQuickSort()
{
	int a[] = { 6,3,5,2,7,8,9,4,1 };
	QuickSort1(a,0, sizeof(a) / sizeof(int)-1);
	PrintArray(a, sizeof(a) / sizeof(int));
}

 

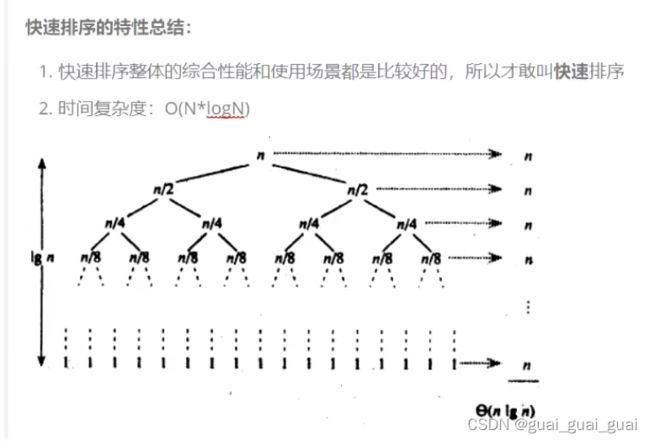
当所排数据有序时，快速排序的时间复杂度最差为O(N^2),因为每次挖的坑都是第一个数或者最后一个数不会有类似二叉树的结构（一次递归左右子树），第一次排用的次数为N，第二次为N-1，第三次为N-2，容易发现此为等差数列，之和近似N^2,故时间复杂度为O(N^2)

为了解决快速排序的最坏情况，可以使用三数取中的方法，找到最左边、最右边以及中间数据的中间值，这样避免了选出的关键数据不会是最大值或者最小值，就避免了一次排序之后没有左边的数据以及右边的数据，导致递归无法同时调用而使时间复杂度增大

int GetMidIndex(int* a, int left, int right)
{
	int mid = (left + right) >> 1;//右移一位，相当于除以2，比除法效率快一点
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
			return mid;
		else if (a[left] > a[right])
			return left;
		else
			return right;
	}
	else
	{
		if (a[right] > a[left])
			return left;
		else if (a[mid] > a[right])
			return mid;
		else
			return right;
	}
}

同时，由于递归会消耗栈帧，递归次数越多，栈帧消耗越大，而且如果左右每次排序均调用递归，越往后，栈帧会指数性的被消耗，所以在这里我们可以先让让快速排序使其接近有序，之后再利用直接插入排序即可，靠后所创建的栈帧就被消除掉了，在这里我是当左右两边数据个数小于10时，使用直接选择排序。

//三数取中
int GetMidIndex(int* a, int left, int right)
{
	int mid = (left + right) >> 1;//右移一位，相当于除以2，比除法效率快一点
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
			return mid;
		else if (a[left] > a[right])
			return left;
		else
			return right;
	}
	else
	{
		if (a[right] > a[left])
			return left;
		else if (a[mid] > a[right])
			return mid;
		else
			return right;
	}
}
//快速排序(1.挖坑法)
int PartSort1(int* a, int left, int right)
{
	int index = GetMidIndex(a, left, right);
	Swap(&a[left], &a[index]);
	int begin = left, end = right;
	int pivot = begin;
	int key = a[begin];
	while (begin < end)
	{
		//右边找小，放到左边
		while (begin < end && a[end] >= key)
		{
			end--;
		}
		//小的放在左边的坑里，自己形成一个新的坑
		a[pivot] = a[end];
		pivot = end;
		//左边找大，放到右边
		while (begin < end && a[begin] <= key)
		{
			begin++;
		}
		//大的放在右边的坑里，自己形成一个新的坑
		a[pivot] = a[begin];
		pivot = begin;
	}
	pivot = begin;
	a[pivot] = key;
	return pivot;
}
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;
	
	int keyindex = PartSort1(a, left, right);
	//[left,keyindex-1]keyindex[keyindex+1,right] 分治递归
	/*QuickSort(a, left, keyindex - 1);
	QuickSort(a, keyindex + 1, right);*/
	if (keyindex - 1 - left > 10)//当左边的数据大于10时，再进行递归调用，小于等于10时，直接插入排序
		QuickSort(a, left, keyindex - 1);//利于减小栈帧的消耗(每进行一次递归调用，都会消耗栈帧，左边和右边同时调用每次消耗的栈帧都会指数性增长)
	else
		InsertSort(a + left, keyindex - 1 - left + 1);
	if (right - (keyindex + 1) > 10)
		QuickSort(a, keyindex + 1, right);//右边同理
	else
		InsertSort(a + keyindex+1, right-(keyindex+1)+1);
}

2.左右指针法

取左边和右边数组的下标，左边找大（比提取数据大），右边找小（比提取数据小）。将左边找的大与右边找的小交换即可，设左索引为begin，右索引为end，二者遍历找合适的数据，最后当begin与end重合时，将关键数据与begin交换即可，最后也可以实现关键数据左边的数据比关键数据小，右边的数据比关键数据大的效果。代码如下：

这里只是单趟排序，最后返回关键数据的下标利用递归实现多次排序。多次排序整体思路和挖坑法相同。

//快速排序(2.左右指针法)
int PartSort2(int* a, int left, int right)
{

	int index = GetMidIndex(a, left, right);
	Swap(&a[left], &a[index]);
	int begin = left, end = right;
	int keyi = begin;
	while (begin < end)
	{
		//找小
		while (begin < end && a[end] >= a[keyi])
			end--;
		//找大
		while (begin < end && a[begin] <= a[keyi])
			begin++;
		Swap(&a[begin], &a[end]);
	}
	Swap(&a[begin], &a[keyi]);
	return begin;//相遇的位置
}

3.前后指针法

这个单趟排序的思路为用prev和cur分别索引，cur用来找比关键数据小的数据，prev和cur最初均指向left，当cur找到比关键数据小的数据时，prev++，将prev数据与cur数据进行交换，这样就保证prev所经过的下标索引的数据均比关键数据小，当cur遍历完整个数组时，此时已经将所有比关键数据小的数据放在prev前面，最后将prev指向的数据与关键数据交换即可。

代码如下：

//快速排序3（前后指针法）
int PartSort3(int* a, int left, int right)
{
	int index = GetMidIndex(a, left, right);
	Swap(&a[left], &a[index]);
	int keyi = left;
	int cur = left, prev = left;
	while (cur <= right)
	{
		if (a[cur] < a[keyi])
		{
			prev++;
			Swap(&a[prev], &a[cur]);
		}
		cur++;
	}
	Swap(&a[keyi], &a[prev]);
	return prev;
}

整体快速排序代码如下：

//三数取中
int GetMidIndex(int* a, int left, int right)
{
	int mid = (left + right) >> 1;//右移一位，相当于除以2，比除法效率快一点
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
			return mid;
		else if (a[left] > a[right])
			return left;
		else
			return right;
	}
	else
	{
		if (a[right] > a[left])
			return left;
		else if (a[mid] > a[right])
			return mid;
		else
			return right;
	}
}
//快速排序(1.挖坑法)
int PartSort1(int* a, int left, int right)
{
	int index = GetMidIndex(a, left, right);
	Swap(&a[left], &a[index]);
	int begin = left, end = right;
	int pivot = begin;
	int key = a[begin];
	while (begin < end)
	{
		//右边找小，放到左边
		while (begin < end && a[end] >= key)
		{
			end--;
		}
		//小的放在左边的坑里，自己形成一个新的坑
		a[pivot] = a[end];
		pivot = end;
		//左边找大，放到右边
		while (begin < end && a[begin] <= key)
		{
			begin++;
		}
		//大的放在右边的坑里，自己形成一个新的坑
		a[pivot] = a[begin];
		pivot = begin;
	}
	pivot = begin;
	a[pivot] = key;
	return pivot;
}
//快速排序(2.左右指针法)
int PartSort2(int* a, int left, int right)
{

	int index = GetMidIndex(a, left, right);
	Swap(&a[left], &a[index]);
	int begin = left, end = right;
	int keyi = begin;
	while (begin < end)
	{
		//找小
		while (begin < end && a[end] >= a[keyi])
			end--;
		//找大
		while (begin < end && a[begin] <= a[keyi])
			begin++;
		Swap(&a[begin], &a[end]);
	}
	Swap(&a[begin], &a[keyi]);
	return begin;//相遇的位置
}
//快速排序3（前后指针法）
int PartSort3(int* a, int left, int right)
{
	int index = GetMidIndex(a, left, right);
	Swap(&a[left], &a[index]);
	int keyi = left;
	int cur = left, prev = left;
	while (cur <= right)
	{
		if (a[cur] < a[keyi])
		{
			prev++;
			Swap(&a[prev], &a[cur]);
		}
		cur++;
	}
	Swap(&a[keyi], &a[prev]);
	return prev;
}
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;
	
	int keyindex = PartSort3(a, left, right);
	//[left,keyindex-1]keyindex[keyindex+1,right] 分治递归
	/*QuickSort(a, left, keyindex - 1);
	QuickSort(a, keyindex + 1, right);*/
	if (keyindex - 1 - left > 10)//当左边的数据大于10时，再进行递归调用，小于等于10时，直接插入排序
		QuickSort(a, left, keyindex - 1);//利于减小栈帧的消耗(每进行一次递归调用，都会消耗栈帧，左边和右边同时调用每次消耗的栈帧都会指数性增长)
	else
		InsertSort(a + left, keyindex - 1 - left + 1);
	if (right - (keyindex + 1) > 10)
		QuickSort(a, keyindex + 1, right);//右边同理
	else
		InsertSort(a + keyindex+1, right-(keyindex+1)+1);
}

三者多次排序代码相同，知识单趟排序思想不同，但都把所选定的关键数据放置排序好之后的位置上。即左边全是比关键数据小的数据，而右边全是比关键数据大的数据。

当然，快速排序也有非递归的做法，下篇博客我再详细介绍吧！